|
30.
Решение линейных уравнений с частными
произ.
Рассмотрим
уравнение
 в предположении, что все коэффициенты
в предположении, что все коэффициенты
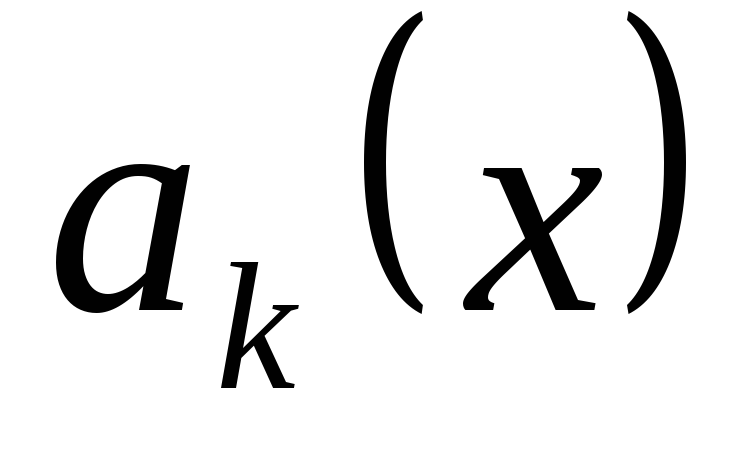 определены в некоторой области D
пространства
определены в некоторой области D
пространства
 ,
непрерывны и непрерывно дифференцируемы
в D,
причём ,
непрерывны и непрерывно дифференцируемы
в D,
причём
 в D.
Введём вектор
в D.
Введём вектор
 .
Составим вектор .
Составим вектор
 и тогда уравнение
и тогда уравнение
 примет вид:
примет вид:
 если
если
 – решение уравнения
– решение уравнения
 ,
то производная этого решения по
направлению ,
то производная этого решения по
направлению
 в каждой точке равна 0.
в каждой точке равна 0.
 задаёт векторное
поле в области D.
Векторные линии этого векторного поля
являются фазовыми траекториями системы
уравнений
задаёт векторное
поле в области D.
Векторные линии этого векторного поля
являются фазовыми траекториями системы
уравнений
 – первый интеграл системы
– первый интеграл системы
 .
Мы установили: всякое решение уравнения .
Мы установили: всякое решение уравнения
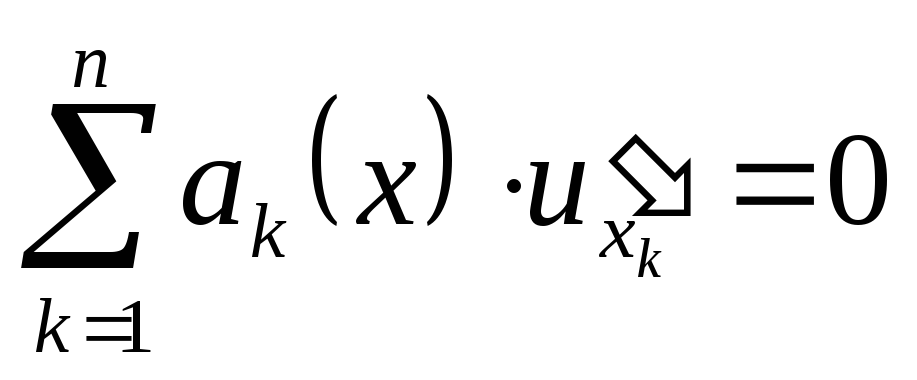 является первым интегралом системы
является первым интегралом системы
 .
Верно и обратное: всякий первый интеграл
системы .
Верно и обратное: всякий первый интеграл
системы
 является решением уравнения
является решением уравнения
 ,
следовательно, чтобы описать всё
множество решений этого уравнения
достаточно описать множество первых
интегралов системы ,
следовательно, чтобы описать всё
множество решений этого уравнения
достаточно описать множество первых
интегралов системы
 . .
Система
 называется характеристической системой
уравнения
называется характеристической системой
уравнения
 .Фазовые
траектории этой системы называется
характеристиками этого уравнения. .Фазовые
траектории этой системы называется
характеристиками этого уравнения.
Через
любую точку области D
проходит единственная характеристика
(система автономна). Точек покоя эта
система не имеет. В этом случае всякая
точка области D
является регулярной.
Для
того, чтобы описать все первые интегралы
системы
 ,
необходимо получить полный набор
функционально независимых первых
интегралов ,
необходимо получить полный набор
функционально независимых первых
интегралов
 .
Отметим, что .
Отметим, что
 функционально независимы, если ранг
матрицы
функционально независимы, если ранг
матрицы
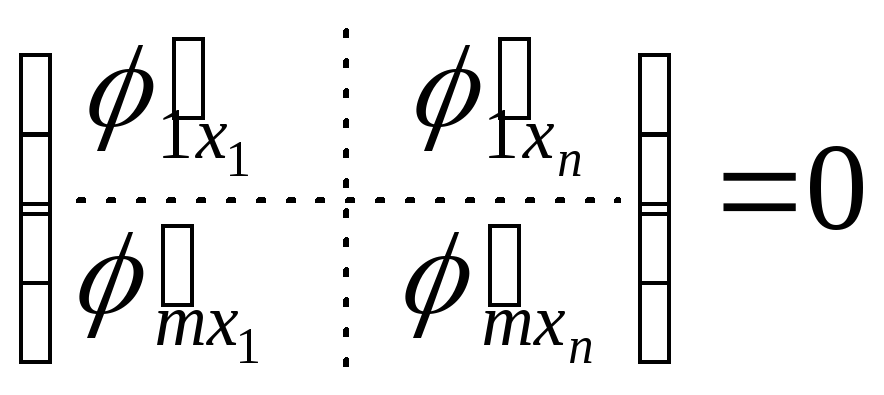 .
Для системы .
Для системы
 ,
состоящей из n
уравнений, полный набор состоит из n
функционалов вида ,
состоящей из n
уравнений, полный набор состоит из n
функционалов вида
 .
Если рассматриваются первые интегралы
вида .
Если рассматриваются первые интегралы
вида
 ,
то полный набор состоит из ,
то полный набор состоит из
 первого интеграла. В общем случае для
наперёд заданной области D
полный набор первых интегралов может
и не существовать. Однако справедливо
следующее утверждение: для любой
нерегулярной точки найдется окрестность,
в которой существует полный набор
функционально независимых первых
интегралов. Пусть D
– такая окрестность, в котором
существует полный набор первых
интегралов. Следовательно, имеем
первые интегралы
первого интеграла. В общем случае для
наперёд заданной области D
полный набор первых интегралов может
и не существовать. Однако справедливо
следующее утверждение: для любой
нерегулярной точки найдется окрестность,
в которой существует полный набор
функционально независимых первых
интегралов. Пусть D
– такая окрестность, в котором
существует полный набор первых
интегралов. Следовательно, имеем
первые интегралы
 ,
следовательно, для любого первого
интеграла ,
следовательно, для любого первого
интеграла
 справедливо представление:
справедливо представление:
 ,
где F
– некоторая функции, следовательно,
любое решение уравнения ,
где F
– некоторая функции, следовательно,
любое решение уравнения
 представляется в виде
представляется в виде
 .
Эта формула задаёт общее решение
уравнения при произвольной
дифференцируемой функции F. .
Эта формула задаёт общее решение
уравнения при произвольной
дифференцируемой функции F.
Характеристическую
систему
 удобно представлять в форме:
удобно представлять в форме:
 . .
|
31.
Решение квазилинейных уравнений
Рассмотрим
уравнение
 в предположении, что
в предположении, что
 и
и
 определены в области
определены в области
 ,
непрерывны и непрерывно дифференцируемы
в D,
причём ,
непрерывны и непрерывно дифференцируемы
в D,
причём
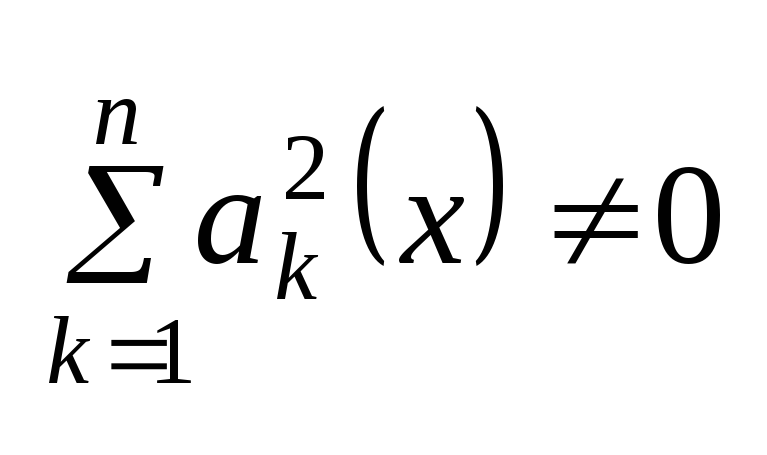 в D.
Сопоставим этому уравнению вспомогательное
линейное уравнение
в D.
Сопоставим этому уравнению вспомогательное
линейное уравнение
 .
Здесь .
Здесь
 .
Это уравнение уже рассмотрено в
предыдущем параграфе, следовательно,
можно написать его общее решение. Оно
получается в неявном виде: .
Это уравнение уже рассмотрено в
предыдущем параграфе, следовательно,
можно написать его общее решение. Оно
получается в неявном виде:
 . .
Составим
характеристическую систему для этого
уравнения:
 .
Пусть .
Пусть
 – функционально независимые первые
интегралы этой системы. Тогда
– функционально независимые первые
интегралы этой системы. Тогда
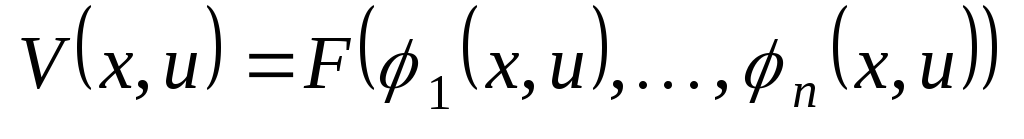 – общее решение уравнения.
– общее решение уравнения.
Пусть
 – решение уравнения
– решение уравнения
 и пусть уравнение
и пусть уравнение
 определяет некоторую функцию
определяет некоторую функцию
 в
в
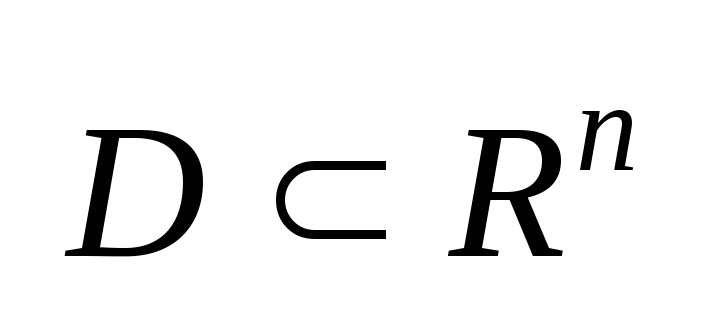 (пространстве x),
причём
(пространстве x),
причём
 .
Тогда .
Тогда
 – решение первого уравнения.
– решение первого уравнения.
Приведённая
теорема устанавливает связь между
решениями уравнений
 и
и
 .
Решения первого уравнения могут
использоваться для неявного задания
решений уравнения второго уравнения.
Если .
Решения первого уравнения могут
использоваться для неявного задания
решений уравнения второго уравнения.
Если
 – решение первого уравнения, то
конечное уравнение
– решение первого уравнения, то
конечное уравнение
 определяет решение второго уравнения.
Множество решений первого уравнения
представляется функцией
определяет решение второго уравнения.
Множество решений первого уравнения
представляется функцией
 ,
следовательно, множество решений
второго уравнения можно описать
решениями уравнения ,
следовательно, множество решений
второго уравнения можно описать
решениями уравнения
 ,
где F
– произвольная функция. Следует иметь
в виду, что функция F
должна обеспечить возможность
разрешения такого уравнения (см.
теорему о неявной функции). На даже в
этом случае мы не можем утверждать,
что таким образом описываются все
решения уравнения ,
где F
– произвольная функция. Следует иметь
в виду, что функция F
должна обеспечить возможность
разрешения такого уравнения (см.
теорему о неявной функции). На даже в
этом случае мы не можем утверждать,
что таким образом описываются все
решения уравнения
 .
Это уравнение может иметь т.н. специальные
решения, не допускающие такого
представления. .
Это уравнение может иметь т.н. специальные
решения, не допускающие такого
представления.
Характеристическая
система, записанная для вспомогательного
уравнения
 называется характеристической системой
исходного уравнения. Через каждую
точку в области проходит единственная
характеристика уравнения
называется характеристической системой
исходного уравнения. Через каждую
точку в области проходит единственная
характеристика уравнения
 .
В отличие от предыдущего параграфа,
характеристики здесь являются линиями
в пространстве переменных .
В отличие от предыдущего параграфа,
характеристики здесь являются линиями
в пространстве переменных
 .
Можно показать, что если через какую-либо
точку интегральной поверхности
проходит характеристика, то вся эта
характеристика лежит на интегральной
поверхности. Интегральная поверхность
как бы «соткана» из характеристик. .
Можно показать, что если через какую-либо
точку интегральной поверхности
проходит характеристика, то вся эта
характеристика лежит на интегральной
поверхности. Интегральная поверхность
как бы «соткана» из характеристик.
|
32Решение
задачи Коши для квазилинейных уравнений
Рассмотрим
уравнение
 ,
предполагая, что ,
предполагая, что
 и
и
 определены в области
определены в области
 ,
непрерывны и непрерывно дифференцируемы
в D
и ,
непрерывны и непрерывно дифференцируемы
в D
и
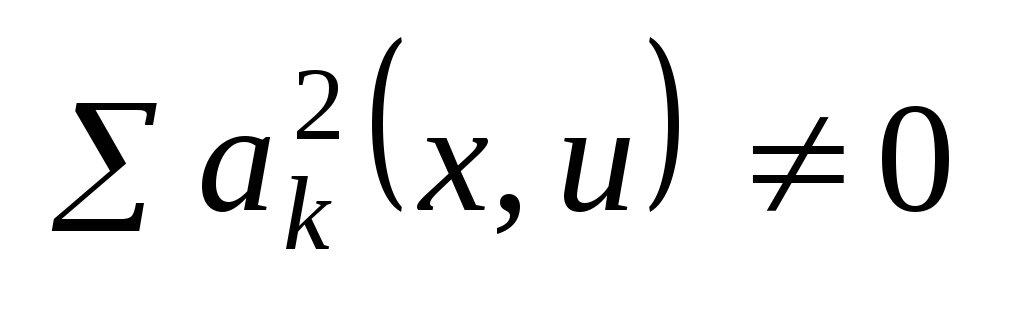 в D.
Можно осуществить выбор решения этого
уравнения, подчинив его каким-либо
дополнительным условиям. В простейшем
случае такими условиями могут быть
условия Коши. Рассмотрим постановку
задачи Коши. Пусть в пространстве x
задана гиперповерхность S:
в D.
Можно осуществить выбор решения этого
уравнения, подчинив его каким-либо
дополнительным условиям. В простейшем
случае такими условиями могут быть
условия Коши. Рассмотрим постановку
задачи Коши. Пусть в пространстве x
задана гиперповерхность S:
 и пусть в точке этой гиперповерхности
определена функция
и пусть в точке этой гиперповерхности
определена функция
 .
Дополним уравнение условием: .
Дополним уравнение условием:
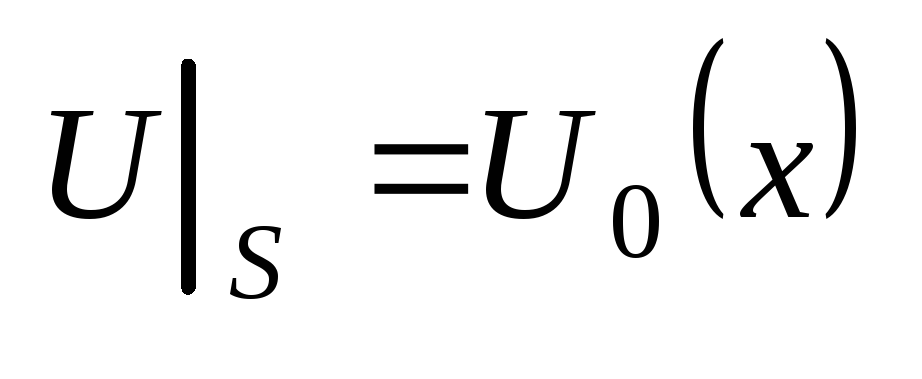 .
Имеем задачу Коши. Решить её значит
найти решение уравнения .
Имеем задачу Коши. Решить её значит
найти решение уравнения
 ,
которое в точке гиперповерхности S
совпадает с заданной функцией ,
которое в точке гиперповерхности S
совпадает с заданной функцией
 .
Нас интересует интегральная поверхность
этого уравнения, содержащая
гиперповерхность S
относительно функции .
Нас интересует интегральная поверхность
этого уравнения, содержащая
гиперповерхность S
относительно функции
 . .
Заметим,
что в общем случае задача Коши может
оказаться разрешимой однозначно,
разрешимой, но не однозначно, или
неразрешимой. Всё зависит от выбора
гиперповерхности S
и начальной функции
 .
Следует иметь в виду, что при сколь
угодно гладкой функции .
Следует иметь в виду, что при сколь
угодно гладкой функции
 решение может и не существовать.
решение может и не существовать.
Простейшим методом
решения задачи Коши является
использование общего решения уравнения
с последующим удовлетворением начальных
условий (если его удаётся построить).
Дополнение:
решение уравнений с помощью рядов.
Рассмотрим
уравнение
 в окрестности точки
в окрестности точки
 . .
Пусть
коэффициенты
 и
и
 аналитичны в окрестности точки
аналитичны в окрестности точки
 ,
причём ,
причём
 .
Тогда решения уравнения .
Тогда решения уравнения
 аналитичны в окрестности точки
аналитичны в окрестности точки
 и могут быть построены в виде ряда
и могут быть построены в виде ряда
 . .
Аналитичность
означает сходимость ряда Тейлора в
окрестности точки
 .
Для нахождения коэффициентов разложения
решения этого уравнения степенной
ряд формально подставляется в уравнение
и собираются коэффициенты при одинаковых
степенях. Получается некоторое
рекуррентное соотношение, из которого
можно найти коэффициенты. .
Для нахождения коэффициентов разложения
решения этого уравнения степенной
ряд формально подставляется в уравнение
и собираются коэффициенты при одинаковых
степенях. Получается некоторое
рекуррентное соотношение, из которого
можно найти коэффициенты.
Пусть
коэффициенты уравнения
 аналитичны в окрестности точки
аналитичны в окрестности точки
 ,
причём ,
причём
 ,
где ,
где
 имеет в точке
имеет в точке
 нуль порядка
нуль порядка
 (если
(если
 ), ),
 имеет в точке
имеет в точке
 нуль порядка
нуль порядка
 (если
(если
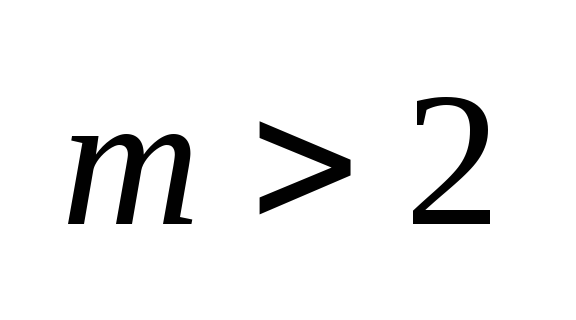 ).
Тогда это уравнение имеет по крайней
мере одно решение, представляемое
обобщённым степенным рядом ).
Тогда это уравнение имеет по крайней
мере одно решение, представляемое
обобщённым степенным рядом
 ,
где
– любая постоянная. ,
где
– любая постоянная.
Рассмотрим
для примера уравнение Бесселя -го
порядка:
 .
Здесь .
Здесь
 .
Можно искать решение в виде обобщённого
ряда .
Можно искать решение в виде обобщённого
ряда
 ,
следовательно, решения такого вида
существуют при ,
следовательно, решения такого вида
существуют при
 – функция Бесселя -го
порядка. Аналогично
– функция Бесселя -го
порядка. Аналогично
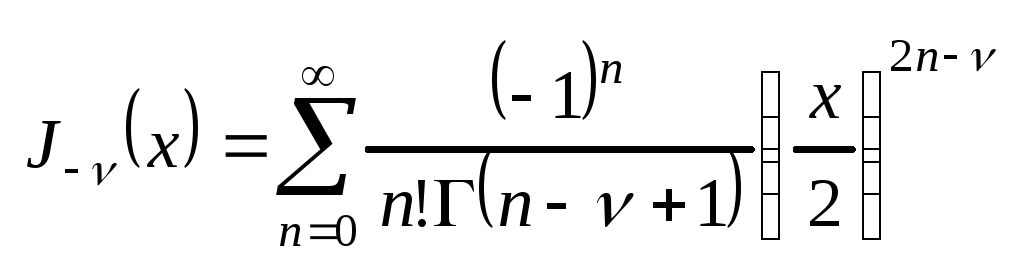 .
При дробных
функции .
При дробных
функции
 и
и
 линейно независимы, следовательно,
они образуют ФСР:
линейно независимы, следовательно,
они образуют ФСР:
 .
При целых .
При целых
 ,
следовательно, они линейно зависимы. ,
следовательно, они линейно зависимы.
В
качестве второго линейного независимого
решения выбираем функцию Неймана
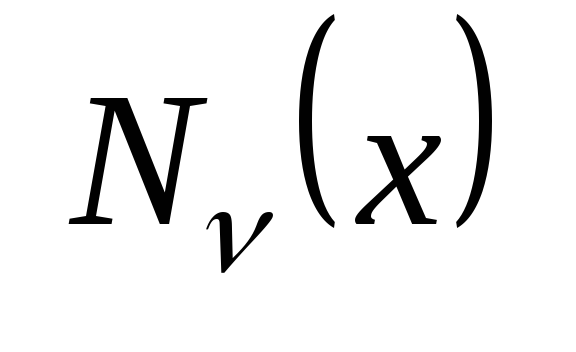 .
Определим её при дробных .
Определим её при дробных
 – дробное. Функции
– дробное. Функции
 и
и
 линейно независимы при
линейно независимы при
 ,
как целых, так и дробных, следовательно,
они образуют ФСР и общее решение: ,
как целых, так и дробных, следовательно,
они образуют ФСР и общее решение:
 . .
|


 .
Для системы
.
Для системы
 .
Пусть
.
Пусть

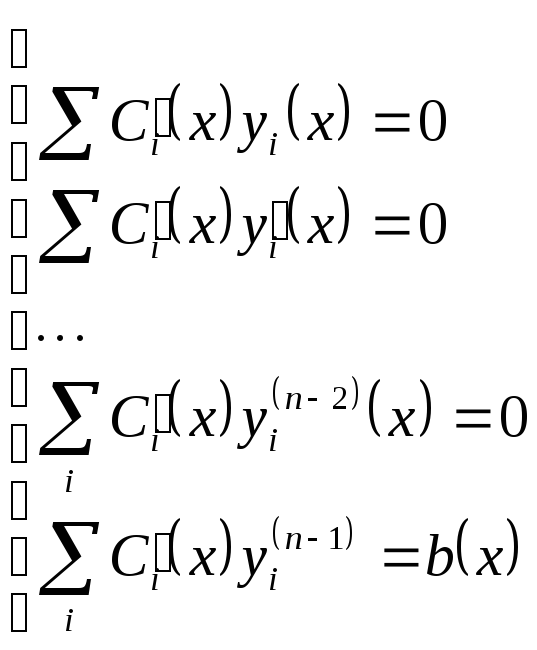 .
В результате мы имеем систему
алгебраических линейных уравнений
относительно
.
В результате мы имеем систему
алгебраических линейных уравнений
относительно
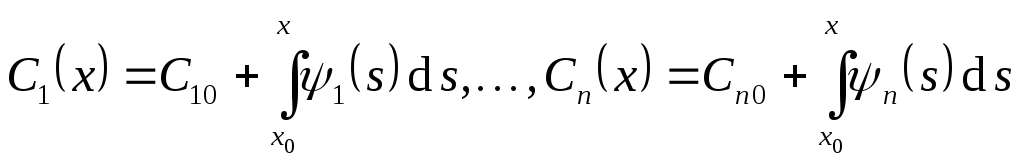 .
Подставляя эти функции в формулу
.
Подставляя эти функции в формулу
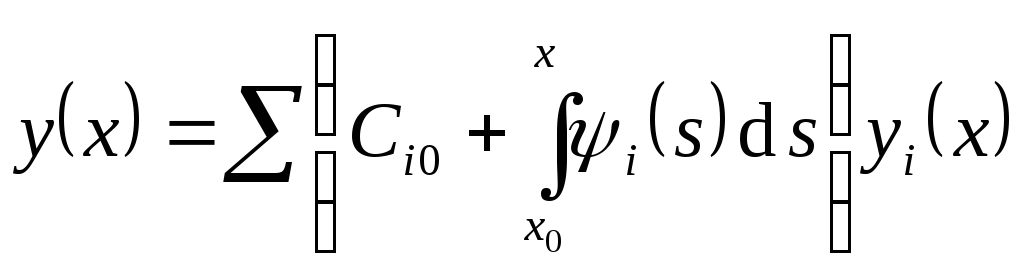 .
Уточним вид функции
.
Уточним вид функции
 ,
где
,
где
 .
Функция
.
Функция
 – частное решение неоднородного
уравнения, но в то же время
– частное решение неоднородного
уравнения, но в то же время