§9.4. Льготные займы и кредиты

Грант-элемент. Предмет обсуждения в данном параграфе также связан с долгосрочными займами. Однако здесь они рас­сматриваются под другим углом зрения. Дело в том, что в ряде случаев долгосрочные займы и кредиты выдаются по тем или иным причинам (иногда политическим) под льготные для заем­щика условия. Низкая (относительно ставки на рынке креди­тов) процентная ставка в сочетании с большим его сроком и льготным периодом дают должнику существенную выгоду, ко­торую можно рассматривать как субсидию. Кредитор в этих ус­ловиях несет некоторые потери, так как он мог бы инвестиро­вать деньги на более выгодных условиях.

Проблема определения размера такого рода помощи обсуж­далась в международных организациях и экономической лите­ратуре главным образом с позиции межстрановых сопоставле­ний — для сравнения размеров финансовой помощи, оказыва­емой ряду развивающихся стран. Однако проблема оценки по­следствий выдачи льготных займов имеет более общее значе­ние, так как льготные займы предоставляют и внутри страны.

Грант-элемент (grant-element) — это условная потеря заимо­давца, которая связана с применением более низкой процент­ной ставки, чем существующие ставки кредитного рынка. Грант-элемент определяется в двух видах: в виде абсолютной и относительной величин.

Абсолютный фант-элемент рассчитывается как разность но­минальной суммы займа и современной величины платежей по погашению займов, рассчитанной по рыночной ставке. Проб­лема, как видим, сводится к выбору надлежащей ставки про­цента для расчета современной величины. Рекомендации по выбору конкретного значения этой ставки весьма расплывчаты. Обычно используют превалирующую на рынке долгосрочных кредитов ставку.

Размер абсолютного грант-элемента находим следующим об­разом:

W=D-G, (9.13)

где W'— абсолютный грант-элемент, D — сумма займа, G — со­временная величина платежей, поступающих в счет погашения займа, рассчитанная по реальной ставке кредитного рынка.

196

Относительный грант-элемент характеризует отношение аб­солютного грант-элемента к сумме займа:

W G

"-Т"¹-^' ^(9Л4)

w — относительный грант-элемент.

Как видим, все переменные приведенных формул определя­ются условиями выдачи и погашения займа.

Выведем рабочие формулы для расчета W и w при условии, что долг и проценты выплачиваются в виде постоянных сроч­ных уплат. Для анализа последствий выдачи льготных займов этого достаточно.

Пусть заем выдан на п лет и предусматривает выплату про­центов по льготной ставке g. На денежном рынке аналогичные по сроку и величине займы выдаются по ставке /. В этом слу­чае при отсутствии льготного периода срочная уплата составит:

Г=-Г", (9.15)

а современная величина всех выплат должника очевидно равна Кяг„._;. В итоге

n\i

а Л

(9.16)

W=D- Ya_ni=D\\-

°n\g I

w-1-7*4 (9.17)

где а .,, а_ио — коэффициенты приведения постоянных годовых рент постнумерандо, определенные для процентных ставок / и

ПРИМЕР 9.10. Льготный заем выдан на 10 лет под 3,8%. Предус­матривается погашение долга равными срочными уплатами. Из­вестно, что обычная рыночная ставка для такого срока займа рав­на 8%. В этом случае

^аю;8 . *-,<_ллв0,038

* 10,3,8 ■ " 1,038

IV = 1 --^- = 1 - 6,71008 х₄ \ _мо__ю = 0,1809.

197

Допустим, исходная сумма займа равна 10 млн руб. Тогда аб­солютный грант-элемент или условная сумма потерь для кредито­ра и, соответственно, выгода для должника, составят

W = 10 х 0,1809 = 1,809 млн руб.

Наличие льготного периода увеличивает фант-элемент. Ес­ли в льготном периоде должник выплачивает проценты, то со­временная величина поступлений по долгу определяется как сумма двух элементов — современных величин процентных платежей в льготном периоде и срочных уплат в оставшееся время. Таким образом,

G= Dgxa_Li+ Yxa_n__L;ixv^L, (9.18)

где п - L — продолжительность периода погашения задолжен­ности; L — продолжительность льготного периода.

После ряда преобразований (9.14) получим¹

G W-1---1-

Ь^-^ ⁺ *^xfld" (9.19)

V ^Un-L;g )

Здесь а_п-щ , ^„-t^ — коэффициенты приведения постоянных рент со сроком п — L и ставками / и g; v^L — дисконтный мно­житель по ставке /.

Обсудим еще один возможный вариант. Пусть в льготном периоде проценты начисляются, но не выплачиваются. Они присоединяются к основному долгу, который погашается в те­чение п — L лет. Условия такого займа более льготны для долж­ника, чем при последовательной выплате процентов.

Срочные уплаты и их современная величина в данном слу­чае равны:

D^+Jt _r-Y п На основе этих выражений получим

w = 1 - — = 1 - — х _t .

D ^an-L* I 1 + I

См. Математическое приложение к главе.

198

ПРИМЕР 9.11. Пусть заем в примере 9.10 предусматривает трехлетний льготный период, в течение которого выплачиваются проценты. Для расчета относительного грант-элемента находим: а₇₈= 5,20637, а₇₃₈= 6,04667, а₃₈= 2,5771,v³ = 1.08"³ = = 0,79383;

w= 1 -

(5,20637

^6,04667

0,79383 + 0,038 х 2,5771 = 0,2185

Если проценты в льготном периоде не выплачиваются, а при­соединяются к основной сумме долга, то

_а 5,20637 |Ч038^з w = 1 - | _л _ | = 0,2356.

6,04667 1 1,08

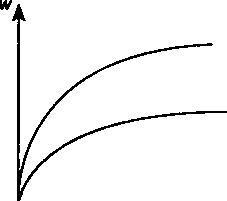
Грант-элемент, как было продемонстрировано выше, — ус­ловная обобщающая характеристика льготности займа (потерь заимодавца и выигрыша должника). Сумма, которая равна грант-элементу, существенно зависит от принятой при ее оп­ределении процентной ставки. График зависимости относи­тельных потерь от соотношения процентных ставок показан на рис. 9.1 для сроков займа 5 и 10 лет без льготного периода, £=5%.

л = 10

2 3

Рис. 9.1

л = 5

i/9

Предельным случаем льготного займа является беспроцент­ный заем. Выдача такого займа связана с потерями, которые оп­ределим, полагая, что соответствующие средства можно было бы разместить под проценты по рыночной ставке /. Например, уже при пятнадцатилетнем сроке беспроцентного займа и рыночной ставке 10% кредитор теряет почти 50% от суммы долга.

199