
- •1. Незатухающие гармонические колебания
- •2. Затухающие гармонические колебания
- •3. Вынужденные колебания
- •5. Биофизика слуха. Звук. Ультразвук.
- •7. Звуковые волны
- •8. Ультразвук
- •11.- 16. Элементы биофизики кровообращения
- •11. І. Реологические свойства крови
- •12. Законы течения вязких жидкостей
- •14. Основные законы гемодинамики
- •16. Распределение среднего давления
- •17. Элементы биомеханики сердца
- •19. Электрические свойства тканей и органов
- •21. Электропроводимость биологических тканей и жидкостей
- •23. Биопотенциалы
- •1.6. Электрокардиография. Реография
- •24. Физические основы реографии
- •25. Основы электротерапии
- •26.Разновидности терапевтических методов
- •28. Тепловое излучение и его характеристики
- •29. Абсолютно черное тело. Серые тела
- •30. Законы теплового излучения
- •31. Тепловое излучение тела человека
- •33. Рентгеновское излучение
- •35. Взаимодействие рентгеновского излучения с веществом
- •37. Методы рентгеновской диагностики
- •38. Элементы радиационной физики. Основы дозиметрии
- •35. Взаимодействие радиоактивных излучений с веществом
- •41. Дозиметрия радиоактивных излучений
1. Незатухающие гармонические колебания
Гармонические колебания совершаются под действием упругих или квазиупругих (подобные упругим) сил, описываемых законом Гука:
![]() ,
,
где F – сила упругости;
х – смещение;
k – коэффициент упругости или жесткости.
Согласно
ІІ
закону Ньютона ![]() ,
где а –
ускорение,
а
=
,
где а –
ускорение,
а
= ![]() .
.
|
|
1 |
Разделим
уравнение (1)
на
массу m
и введем обозначение ![]() ,
получим
уравнение
в виде:
,
получим
уравнение
в виде:
![]() 2
2
Уравнение (2) – дифференциальное уравнение незатухающих гармонических колебаний.
Его
решение имеет вид:
![]() или
или ![]() .
.
Характеристики незатухающих гармонических колебаний:
х
–
смещение;
А
– амплитуда;
Т
– период;
![]() – частота;
– частота;
![]() – циклическая
частота,
– циклическая
частота, ![]() – скорость;
– скорость; ![]() – ускорение,
– ускорение, ![]() – фаза;
– фаза; ![]() 0
– начальная фаза, Е
–
полная
энергия.
0
– начальная фаза, Е
–
полная
энергия.
Формулы:
|
|
|
|
|
|
|
|
|
|
2. Затухающие гармонические колебания
В реальных системах, участвующих в колебательном движении, всегда присутствуют силы трения (сопротивления):
![]() ,
,
![]() – коэффициент сопротивления;
– коэффициент сопротивления; ![]() –
скорость.
–
скорость.
![]() .
.
Тогда ІІ закон Ньютона запишем:
![]()
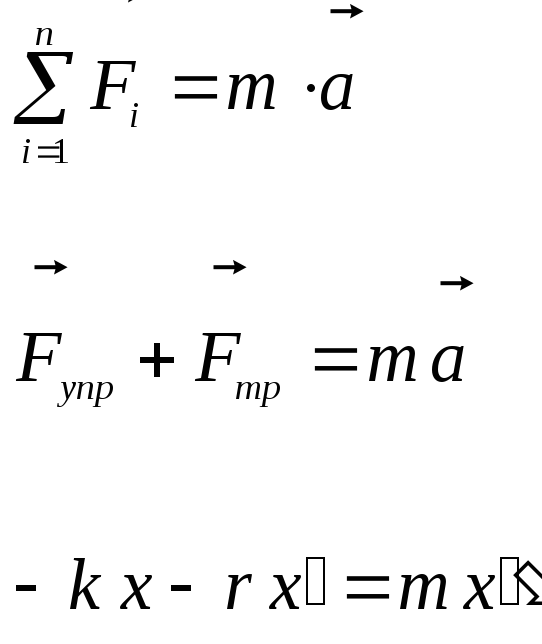
|
|
(2) |
Введем
обозначения ![]() ,
,
![]() ,
где
,
где ![]() – коэффициент затухания.
– коэффициент затухания.
Уравнение (2) запишем в виде:
|
|
(3) |
Уравнение (3) – дифференциальное уравнение затухающих колебаний.
Его
решение ![]() ,
где
,
где
![]() –амплитуда
колебаний в начальный момент времени;
–амплитуда
колебаний в начальный момент времени;
![]() –циклическая
частота затухающих колебаний.
–циклическая
частота затухающих колебаний.
Амплитуда колебаний изменяется по экспоненциальному закону:
![]() .
.
|
|
|
Характеристики:
1) ![]() – период затухающих колебаний; 2)
– период затухающих колебаний; 2) ![]() – частота затухающих колебаний;
– частота затухающих колебаний;
![]() –
собственная частота колебательной
системы;
–
собственная частота колебательной
системы;
3) логарифмический
декремент затухания (характеризует
скорость убывания амплитуды): ![]() .
.
3. Вынужденные колебания
Для получения незатухающих колебаний необходимо воздействие внешней силы, работа которой восполняла бы вызванное силами сопротивлений уменьшение энергии колеблющейся системы. Такие колебания называются вынужденными.
Закон
изменения внешней силы: ![]() ,
где
,
где ![]() – амплитуда внешней силы.
– амплитуда внешней силы.
ІІ закон Ньютона запишем в виде
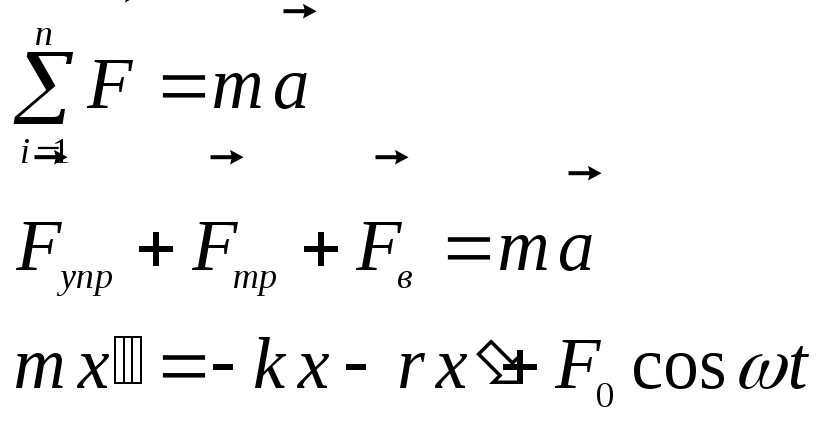
Введем
обозначения ![]() .
.
Уравнение вынужденных колебаний имеет вид:
![]() .
.
Решение этого уравнения в установившемся режиме:
![]() ,
,
|
где |
(4) |
![]()
![]() –частота вынужденных
колебаний.
–частота вынужденных
колебаний.
Из
формулы (4), когда ![]() ,
амплитуда достигает максимального
значения.
,
амплитуда достигает максимального
значения.
Это явление называется резонансом.
![]()
5. Биофизика слуха. Звук. Ультразвук.
Волна – это процесс распространения колебаний в упругой среде.
Уравнение волны выражает зависимость смещения колеблющейся точки, участвующей в волновом процессе, от координаты ее равновесного положения и времени: S = f (x ;t).
![]()
![]()
"0" x x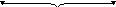

r
Рис. 13
Если S и X направлены вдоль одной прямой, то волна продольная, если они взаимно перпендикулярны, то волна поперечная.
Уравнение
в точке "0" имеет вид ![]() .
Фронт волны дойдет до точки "х"
с запаздыванием за время
.
Фронт волны дойдет до точки "х"
с запаздыванием за время ![]() .
.
Уравнение
волны имеет
вид ![]() .
.
Характеристики волны:
S
– смещение, А
– амплитуда, ![]() – частота, Т
– период,
– частота, Т
– период, ![]() – циклическая частота,
– циклическая частота, ![]() – скорость.
– скорость.
![]() –фаза волны,
–фаза волны, ![]() – длина волны.
– длина волны.
Длиной
волны
называется расстояние между двумя
точками, фазы которых в один и тот же
момент времени отличаются на ![]() .
.
![]()
Фронт волны – совокупность точек имеющих одновременно одинаковую фазу.
Поток энергии равен отношению энергии, переносимой волнами через некоторую поверхность, к времени, в течении которого эта энергия перенесена:
![]() ,
, ![]() .
.
Интенсивность:
![]() ,
,
![]() –
площадь,
–
площадь,
![]() .
.
Вектор интенсивности, показывающий направление распространения волн и равный потоку энергии волн через единичную площадь, перпендикулярную этому направлению, называется вектором Умова.
![]() –плотность
вещества.
–плотность
вещества.

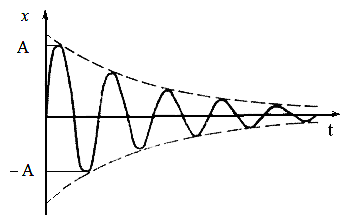 Рис. 11. График
x=f(t)
Рис. 11. График
x=f(t)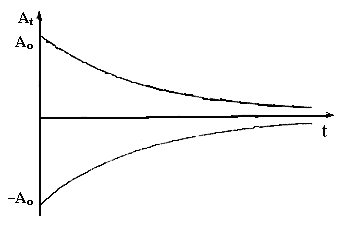 Рис. 12.
График At=f(t)
Рис. 12.
График At=f(t)