Параметр потока отказов

Этот показатель также характеризует восстанавливаемый объект и по статистическим данным определяется с помощью формулы:

(15)

где n(t₁) и n(t₂) - количество отказов объекта, зафиксированных соответственно, по истечении времени t₁ и t₂.

Если используются данные об отказах по определенному количеству восстанавливаемых объектов, то

(16)

где - количество отказов по всем объектам за интервал времени; N_о - количество однотипных объектов, участвующих в эксперименте (отказавший объект восстанавливается, N_о = соnst).

Параметр потока отказов представляет собой плотность вероятности возникновения отказа восстанавливаемого объекта. Отказы объектов возникают в случайные моменты времени и в течение заданного периода эксплуатации наблюдается поток отказов. Существует множество математических моделей потоков отказов. Наиболее часто при решении задач надежности электроустановок используют простейший поток отказов - пуассоновский поток. Простейший поток отказов удовлетворяет одновременно трем условиям: стационарности, ординарности, отсутствия последствия.

Стационарность случайного процесса (времени возникновения отказов) означает, что на любом промежутке времени вероятность возникновения n отказов зависит только от n и величины промежутка, но не зависит от сдвигапо оси времени.

Ординарность случайного процесса означает, что отказы являются событиями случайными и независимыми. Ординарность потока означает невозможность появления в один и тот же момент времени более одного отказа.

Отсутствие последствия означает, что вероятность наступления n отказов в течение промежутка не зависит от того, сколько было отказов и как они распределялись до этого промежутка. Следовательно, факт отказа любого элемента в системе не приведет к изменению характеристик (работоспособности) других элементов системы, если даже система и отказала из-за какого-то элемента.

Опыт эксплуатации сложных технических систем показывает, что отказы элементов происходят мгновенно и если старение элементов отсутствует ( (t) = const), то поток отказов в системе можно считать простейшим.

Случайные события, образующие простейший поток, распределены по закону Пуассона [4,13, 15]:

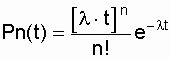при n ≥ 0 (17)

где Рn(t) - вероятность возникновения в течение времени t ровно n событий (отказов); λ - параметр распределения, совпадающий с параметром потока событий.

Если в выражении (17) принять n = 0, то получим - вероятность безотказной работы объекта за время t при интенсивности отказов  = const. Нетрудно доказать, что если восстанавливаемый объект при отсутствии восстановления имеет характеристику  = const, то, придавая объекту восстанавливаемость, мы обязаны записать w(t) = const;  = w . Это свойство широко используется в расчетах надежности ремонтируемых устройств. В частности, важнейшие показатели надежности оборудования электроустановок даны в предположении простейших потоков отказов и восстановлений, когдаи соответственно.

Комплексные позатели надежности

Параметр потока отказов и наработка на отказ характеризуют надежность ремонтируемого изделия и не учитывают времени, необходимого на его восстановление. Поэтому они не характеризуют готовности изделия к выполнению своих функций в нужное время. Для этой цели и введены комплексные показатели надежности

К числу комплексных показателей надежности, наиболее часто употребляемых для оценки надежности восстанавливаемых изделий, следует отнести:

1. коэффициент готовности - К_г;

2. коэффициент вынужденного простоя - К_п;

3. коэффициент оперативной готовности - К_о.г.;

4. коэффициент технического использования - К_т.и.;

5. средний недоотпуск электроэнергии – ΔЭ;

6. средний ущерб на один отказ;

7. удельный ущерб.

Коэффициент готовности характеризует частично совокупность свойств безотказности и ремонтопригодности и представляет собой вероятность того, что изделие окажется работоспособным в произвольный момент времени t.

В практических задачах обычно используют стационарное значение коэффициента готовности К_г, к которому стремится функция К_г(t) при t → ∞:

К_г = lim К_г(t) = t_р /( t_р + t_п), (1)

т.е. стационарное значение К_г это есть отношение времени исправной работы t_р к сумме времен исправной работы и вынужденных простоев изделия t_п , взятых за один и тот же календарный срок.

Времена t_р и t_п вычисляются по формулам

t_р = ∑t_pi ;t_п =∑t_ni ,

где - t_рi – время работы изделия между (i -1) - м и i – м отказом; t_пi – время вынужденного простоя после i – го отказа; n – число отказов (ремонтов) изделия.

Выражение (1) является статистическим определением коэффициента готовности. Для перехода к вероятностной трактовке К_г величины t_р и t_п заменяются математическими ожиданиями времени между соседними отказами и времени восстановления соответственно. Тогда

К_г = t_ср /( t_ср + t_в),

где - t_ср – наработка на отказ; t_в – среднее время восстановления.

Коэффициентом вынужденного простоя называется отношение времени вынужденного простоя к сумме времен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок. Согласно определению

К_п = t_п /( t_р + t_п),

или, переходя к средним величинам,

К_п = t_в /(t_ср + t_в).

Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью

К_г(t) = 1 - К_п(t)

При анализе надежности восстанавливаемых систем обычно коэффициент готовности вычисляют по формуле

К_г = Т_ср /( Т_ср+ t_в) (2)

Выражение верно только в том случае, если поток отказов простейший, и тогда t_ср = Т_ср

Для выяснения физического смысла К_г запишем выражение для вероятности застать систему в исправном состоянии. При этом рассмотрим наиболее простой случай, когда интенсивность отказов и интенсивность восстановления есть величины постоянные. Предполагая, что при t =0 система находится в исправном состоянии ( Р(0) =1), вероятность застать систему в исправном состоянии определяется выражением:

Р_г(t) =μ/(λ+ μ) + λ/( λ+ μ)*e^-( λ+ μ)t

,

P_г(t)=K_г+(1- K_г) e^-t/ K_гt_в

где- .

λ=1/Т_ср; μ=1/t_в; K_г= Т_ср/( Т_ср+ t_в)

Это выражение устанавливает зависимость между коэффициентом готовности системы и вероятностью застать ее в исправном состоянии в любой момент времени t.

В некоторых случаях критериями надежности восстанавливаемых систем могут быть также критерии надежности не восстанавливаемых систем, например: ВБР, частота отказов, средняя наработка до первого отказа, интенсивность отказов. Такая необходимость возникает всегда, когда имеет смысл оценить надежность восстанавливаемой системы до первого отказа, а также в случае, когда применяется резервирование с восстановлением отказавших резервных устройств в процессе работы системы, отказ всей резервированной системы не допускается.

Коэффициент оперативной готовности – вероятность того, что изделие проработает безотказно на интервале (t_,t + τ); для объектов электрических систем этот коэффициент определяется выражением

К_о.г.= К_г е ^-λt

Коэффициент технического использования. Этот показатель харак­теризует те же свойства, что и коэффициент готовности, но учитывает до­полнительно время проведения предупредительных ремонтов и представляет собой отношение математического ожидания времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к сумме математических ожиданий времени пребывания объекта в работоспособном состоянии, времени простоев, обусловленных техническим обслуживанием, и времени ремонтов за тот же период эксплуатации, т. е.

К_т.и. = Т _СР / (Т_СР +t_В +τ)

где т - математическое ожидание времени нахождения объекта в отключен­ном состоянии для производства профилактических работ.

Средний недоотпуск электроэнергии ∆Э. Этот показатель характеризует не только все основные свойства надежности системы, но и режим ее загруз­ки, и представляет собой математическое ожидание недоотпуска электро­энергии потребителям за расчетный период времени. Его оценка для узлов нагрузки и системы в целом является одной из конечных целей расчетов надежности.

Рассмотрим суть оценки недоотпуска электроэнергии. Пусть в процес­се эксплуатации объекта в момент t наступил отказ, в то время как нагрузка потребителя составляла величину W_П. В общем случае отказ системы по от­ношению к рассматриваемому потребителю может быть не полным, а час­тичным, когда система способна удовлетворять не всю нагрузку, а только часть ее w_R. Недоотпуск электроэнергии при этом может быть найден как

∆Э =

где интервал времени (t –t₁) - время дефицита энергии и интегрирование осуществляется только в области времени положительных дефицитов, т. е. когда D(t)> 0:

D(t) = W_П(t) – W_R.

В практических расчетах интеграл заменяется суммой

∆Э =∑(W_п(t)- W_R)∆t

где W_П(t) - среднечасовая текущая нагрузка потребителя в момент t, оп­ределяемая по ожидаемому графику нагрузки в день аварии, ∆t = 1 час.

Недоотпуск электроэнергии за время Т потребителям узла нагрузки при полном прекращении его электроснабжения можно определить по формуле

∆Э =W_П-K_П = P_ПT,K_П,

где P_П,W_П - соответственно математическое ожидание мощности и энергии, потребляемой узлом нагрузки за время Т; К_П - коэффициент вынужденного простоя системы относительно узла нагрузки (средняя вероятность состояния отказа).

Экономический ущерб от ненадежности. Этот показатель надежно­сти является наиболее полным. Он характеризует интегрально все свойства надежности системы, включая режим ее загрузки и значимость потребителя энергии. Важность каждого потребителя с экономической точки зрения ха­рактеризуется величиной удельного ущерба [У₀ руб/(кВт • ч)].

Экономический ущерб при каждом отказе k (k = 1,2, ... п) за некото­рый период Т

У_К = У₀∆Э_К

В том случае, когда ущерб зависит еще и от глубины ограничения по­требителя по мощности, определение его усложняется из-за необходимости расчетов по ступенчатой зависимости удельных ущербов.

средний ущерб на один отказ – математическое ожидание ущерба; удельный ущерб – ущерб, отнесенный либо к единице недоотпущенной электроэнергии, либо к единице ограничиваемой энергии, либо к единице времени. Эти показатели используются в технико – экономических расчетах, когда возникает необходимость экономической оценки надежности.