1.3. Приведение общей задачи лп к канонической форме

В тех случаях, когда в задаче ЛП три и более переменных используют для решения симплексный метод. Этот метод является универсальным и предназначен для решения задачи ЛП в канонической форме.

Определение.В случае, когда все ограничения (1.2) в задаче ЛП являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называютканонической.

Она может быть представлена в координатной, векторной или матричной форме записи.

а) каноническая задача ЛП в координатной форме имеет вид:

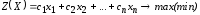; (1.6)

,.

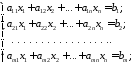
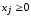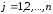Данную задачу можно записать, используя знак суммирования:

,

,

,,.

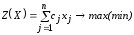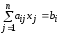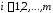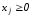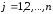б) каноническая задача ЛП в векторной форме имеет вид: ,

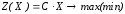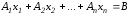, (1.7)

,

где ;;

,;;.

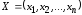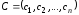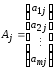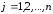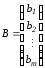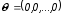в) каноническая задача ЛП в матричной форме имеет вид:

,

,,

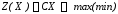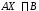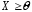где ,,.

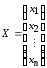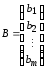При составлении математических моделей экономических задач ограничения в основном формируются в системы неравенств. Поэтому необходимо уметь переходить от них к системам уравнений. Например, рассмотрим линейное неравенство

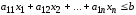(1.8)

и прибавим к его левой части некоторую величину 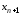такую, чтобы неравенство превратилось в равенство.

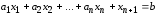, (1.9)

где .

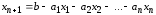Неотрицательная переменная 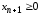называется дополнительной переменной. Следующая теорема даёт основание для возможности такого преобразования.

Теорема 1.1.Каждому решению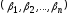неравенства (1.8) соответствует единственное решение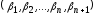уравнения (1.9) и неравенства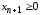, и, наоборот, каждому решению уравнения (1.9)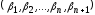с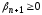соответствует решение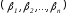неравенства (1.8).

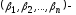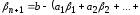
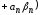Доказательство.Пустьрешение неравенства (1.8). Тогда. Возьмём число. Ясно, что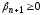. Подставив в уравнение (1.9), получим

.

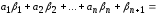
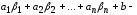
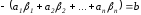Первая часть теоремы доказана.

Пусть теперь векторудовлетворяет уравнению (1.9) с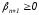, т.е.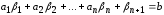. Отбрасывая в левой части последнего равенства неотрицательную величину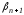, получаем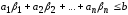, и т.д.

Таким образом, доказанная теорема фактически устанавливает возможность приведения всякой задачи ЛП к каноническому виду. Для этого достаточно в каждое ограничение, имеющее вид неравенства, ввести свою дополнительную неотрицательную переменную. Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому на её значение не влияют.

1.4. Свойства решений задач линейного программирования

Одним из основных понятий в теории ЛП является многогранник в - мерном пространстве и угловая точка. Перейдём к их определению.

Пусть 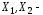две произвольные (различные) точки пространства.

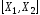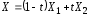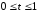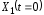Определение.Отрезкомназывается множество всех точек извида, где. Точкии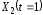называются концами отрезка, остальные точки называются внутренними.

Определение. Множество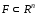называется выпуклым, если оно содержит вместе с каждыми двумя точками весь отрезок, содержащий эти точки.

Теорема 1.2.Пересечение выпуклых множеств есть выпуклое множество.

Доказать самостоятельно.

_{Определение.} Гиперплоскостью в пространстве _{называется совокупность точек 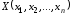, удовлетворяющих уравнению}

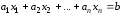, (1.10)

где хотя бы один из коэффициентов 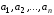отличен от нуля.

_{Определение.} Полупространством в _{называется множество точек}

_{, удовлетворяющих неравенству}

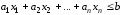(1.11)

или неравенству

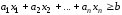. (1.12)

_{Ясно, что гиперплоскость (1.10) есть пересечение полупр}остранств (1.11) и (1.12). Обозначая черезАвектор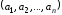, мы получим краткую запись гиперплоскости (1.10):AX=Bи полупространств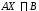,. _{Теперь легко доказать следующую теорему:}

Теорема 1.3.Всякое полупространство в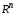является выпуклым множеством.

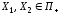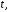
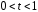
_{Доказательство. Рассмотрим}. Пусть _{и пусть для произвольного 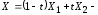любая точка отрезка.}

.

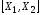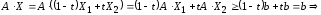
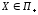Следствие. Всякая гиперплоскость в является выпуклым множеством.

Определение. Пересечение конечного числа полупространств называетсямногогранной областью.

Определение. Ограниченная многогранная область называетсямногогранником.

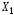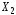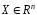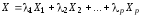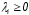Определение. Выпуклой линейной комбинацией векторов,, …,называется всякий вектор, допускающий представление, гдеи.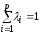

Определение.Точка множества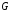называется угловой точкой, если она не является внутренней точкой отрезка, целиком принадлежащего.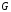

Угловые точки многогранника называются его вершинами.

Теорема 1.4.Любая точка многогранника является выпуклой линейной комбинацией его угловых точек.

Теорема 1.5.(основная теорема ЛП). Целевая функция задачи ЛП достигает экстремума в угловой точке множества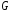допустимых решений , причём если целевая функция достигает экстремума в нескольких угловых точках множества допустимых решений, то она также достигает экстремума в любой выпуклой линейной комбинации этих точек.

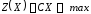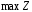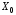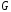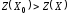
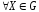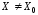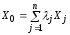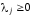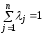Доказательство. Будем считать, что решается задача на максимум целевой функции, т.е. при системе ограничений (1.2). Доказательство проведём методом от противного. Предположим, чтодостигается во внутренней точкемногогранника, т.е.,. Тогда по теореме1.4,и, где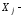угловые точки многогранника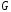. Найдём

.

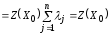
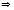
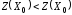Получено противоречие. Следовательно, 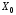является угловой точкой области допустимых решений.

Докажем второе утверждение теоремы. Пусть угловые точки 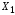,,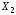 …,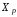являются оптимальными решениями, т.е.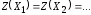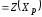и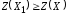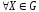. Найдём значение целевой функции для некоторой выпуклой линейной комбинации этих угловых точек:,,,.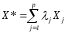

,

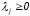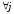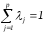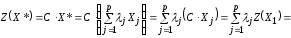
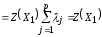т.е. решение 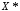также является оптимальным.

Рассмотрим каноническую задачу ЛП в векторной записи (см.(1.7)):

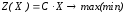
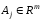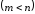,,(1.13)

.

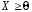Определение. Опорным решением задачи ЛПназывается такое допустимое решение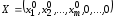, для которого соответствующие положительным координатам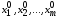векторы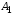,,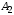…,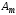в (1.13) линейно независимы.

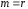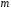Число отличных от нуля координат опорного решения не может быть больше ранга системы векторов условия (т.е. числа линейно независимых уравнений системы ограничений). В дальнейшем будем считать, что система ограничений состоит из линейно независимых уравнений, т.е.. Если число отличных от нуля координат опорного решения равно, то оно (решение) называется невырожденным, в противном случае (меньше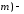вырожденным.

Определение. Базисом опорного решения называется базис системы векторов условия задачи (1.13), в состав которого входят векторы, соответствующие отличным от нуля координатам опорного решения.

Приведём без доказательства теоремы о взаимосвязи опорных решений и угловых точек множества допустимых решений.

Теорема 1.6. Любое опорное решение является угловой точкой области допустимых решений и наоборот, любая угловая точка области допустимых решений является опорным решением.