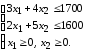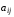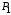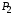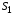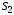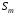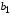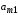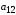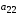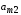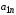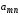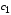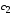- •М. М. Цвиль
- •Оглавление
- •Предисловие
- •Раздел 1. Математическое программирование Глава 1. Линейное программирование
- •1.1. Формы модели задач линейного программирования
- •1.2. Графический метод решения задач линейного программирования
- •1.3. Приведение общей задачи лп к канонической форме
- •1.4. Свойства решений задач линейного программирования
- •1.5. Симплексный метод решения задач линейного программирования
- •1.6. Метод искусственного базиса
- •Глава 2. Двойственные задачи
- •2.1. Построение двойственной задачи
- •2.2. Одновременное решение прямой и двойственной задач
- •Глава 3. Транспортная задача
- •3.1. Постановка задачи и её математическая модель
- •3.2. Особенности решения транспортных задач с неправильным балансом:
- •3.3. Построение первоначального опорного плана
- •3.4. Метод потенциалов
- •Контрольные вопросы и задания
1.1. Формы модели задач линейного программирования
Построение математической модели изучаемого процесса включает в себя следующие этапы:
1) выбор переменных задачи;
2) составление системы ограничений;
3) выбор целевой функции.
Переменнымизадачи называют величины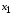 ,
,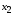 ,…,
,…, ,
которые полностью характеризуют
изучаемый процесс. Их обычно записывают
в виде вектора
,
которые полностью характеризуют
изучаемый процесс. Их обычно записывают
в виде вектора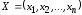 .
.
Система ограниченийвключает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий.
Целевой функциейназывают функцию переменных задачи, экстремум которой требуется найти.
В общем случае задача ЛП может быть записана в виде:
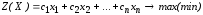 ,
(1.1)
,
(1.1)
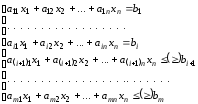 (1.2)
(1.2)
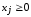 ,
,
 ,
(1.3)
,
(1.3)
т.е. требуется найти
экстремум целевой функции (1.1) и
соответствующие ему значения переменных
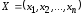 при условии, что переменные удовлетворяют
системе ограничений (1.2) и условию
неотрицательности (1.3).
при условии, что переменные удовлетворяют
системе ограничений (1.2) и условию
неотрицательности (1.3).
Приведем математическую модель задачи использования ресурсов.
Для изготовления нескольких видов
продукции
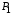 ,
,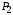 ,…,
,…,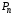 используют
используют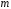 видов ресурсов
видов ресурсов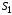 ,
,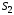 ,…,
,…,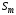 (например, различные материалы,
электроэнергию и т.д.). Объём каждого
вида ресурсов ограничен и известен:
(например, различные материалы,
электроэнергию и т.д.). Объём каждого
вида ресурсов ограничен и известен: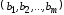 .
Известно также
.
Известно также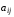
 количество
каждого
количество
каждого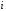 -го
вида ресурса, расходуемого на производство
единицы
-го
вида ресурса, расходуемого на производство
единицы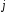 -го
вида продукции. Кроме того, известна
прибыль, получаемая от реализации
единицы каждого вида продукции
-го
вида продукции. Кроме того, известна
прибыль, получаемая от реализации
единицы каждого вида продукции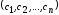 .
Условие задачи можно представить в виде
табл. 1.1.
.
Условие задачи можно представить в виде
табл. 1.1.
Таблица 1.1
|
Вид ресурсов |
Объём ресурсов |
| |||
|
|
|
. . . |
| ||
|
. . .
|
. . .
|
. . .
|
. . .
|
. . . . . . . . . . . . . . . . . . |
. . .
|
|
Прибыль |
|
|
. . . |
| |
Пусть
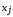
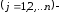 количество
каждого вида продукции, которое необходимо
произвести. Для первого ресурса имеет
место неравенство-ограничение
количество
каждого вида продукции, которое необходимо
произвести. Для первого ресурса имеет
место неравенство-ограничение
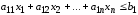 .
.
Аналогичные неравенства будут и для
остальных видов ресурсов. Следует
учитывать, что все значения
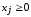 ,
,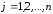 .
.
Общая прибыль, получаемая от реализации
всей продукции может быть представлена
как функция
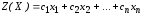 ,
для которой нужно найти максимальное
значение. Таким образом, математическая
модель задачи использования ресурсов
запишется в виде:
,
для которой нужно найти максимальное
значение. Таким образом, математическая
модель задачи использования ресурсов
запишется в виде:
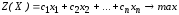 ,
,
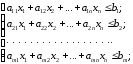 (1.4)
(1.4)
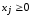 ,
,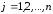 .
.
Пример 1.1.Фирма производит две
модели А и В сборных книжных полок. Их
производство ограничено наличием сырья
(высококачественных досок) и временем
машинной обработки. Для каждого изделия
модели А требуется 3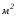 досок, а для изделия модели В – 4
досок, а для изделия модели В – 4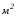 .
Фирма может получить от своих поставщиков
до 1700
.
Фирма может получить от своих поставщиков
до 1700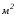 досок в неделю. Для каждого изделия
модели А требуется 12 мин. машинного
времени, а для изделия модели В – 30 мин.
В неделю можно использовать 160 ч машинного
времени. Сколько изделий каждой модели
следует фирме выпускать в неделю, если
каждое изделие модели А приносит 2 дол.
прибыли, а каждое изделие модели В – 4
дол. прибыли?
досок в неделю. Для каждого изделия
модели А требуется 12 мин. машинного
времени, а для изделия модели В – 30 мин.
В неделю можно использовать 160 ч машинного
времени. Сколько изделий каждой модели
следует фирме выпускать в неделю, если
каждое изделие модели А приносит 2 дол.
прибыли, а каждое изделие модели В – 4
дол. прибыли?
Составим математическую модель. Пусть
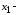 количество
выпущенных за неделю полок модели А, а
количество
выпущенных за неделю полок модели А, а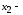 количество
выпущенных за неделю полок модели В.
Еженедельная прибыль выражается целевой
функцией
количество
выпущенных за неделю полок модели В.
Еженедельная прибыль выражается целевой
функцией .
Ограничение, наложенное на объём
используемого сырья, выражается
неравенством
.
Ограничение, наложенное на объём
используемого сырья, выражается
неравенством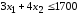 ,
а на количество машинного времени –
,
а на количество машинного времени –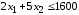 .
Задача состоит в том, чтобы найти
наилучшие значения
.
Задача состоит в том, чтобы найти
наилучшие значения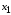 и
и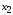 .
Очевидно, наилучшими для данной задачи
являются такие значения, которые
максимизируют еженедельную прибыль.
.
Очевидно, наилучшими для данной задачи
являются такие значения, которые
максимизируют еженедельную прибыль.
Итак, нужно максимизировать функцию
 при следующей системе ограничений:
при следующей системе ограничений: