20. В правильной четырехугольной пирамиде апофема равна l, а плоский угол при вершине . Найдите объем конуса, описанного около пирамиды.

21. Основание пирамиды - ромб с тупым углом , двугранные углы при основании. Найдите объем пирамиды, если радиус вписанного шара равенr.

22. Около шара описан усеченный конус, площадь осевого сечения которого s, острый угол сечения . Найдите объем шара.

23. Равнобедренный треугольник, основание которого равно а и острый угол при вершине равен 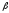, вращается около прямой, которая лежит в плоскости треугольника и проходит через вершину углаперпендикулярно к боковой его стороне. Найдите объем тела вращения.

24. Прямоугольный треугольник с катетом а и прилежащим к нему углом 30° вращается вокруг оси, проходящей через вершину данного угла перпендикулярно гипотенузе. Найдите площадь поверхности тела вращения.

25. Основание пирамиды равнобокая трапеция с основаниями а и b; двугранные углы при основании . Найдите объем вписанного шара.

26. Сторона основания правильной треугольной пирамиды равна а. Боковое ребро наклонено к основанию под углом . Найдите объем вписанного шара. Варіант 18

Описати методику розв’язання задачі. Для виділених задач побудувати зображення комбінацій тіл.

1. Если у трехгранного угла два плоских острых угла равны, то проекция их общей стороны на противолежащую грань будет биссектрисой третьего плоского угла. Докажите.

2. Одна из диагоналей ромба равна 40 см, а его площадь 600 см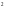. Расстояние от некоторой точки пространства до плоскости ромба равно 16 см. Расстояния от данной точки до каждой стороны ромба равны. Вычислите это расстояние.

3. В прямоугольном треугольнике перпендикуляр, проведенный из вершины прямого угла, равен 24 см и делит гипотенузу в отношении 9:16. Расстояние от точки пространства до вершин треугольника равно 65 см. Вычислите расстояние от этой точки до плоскости этого треугольника.

4. Трапеция вписана в круг, причем меньшее ее основание, равное 5см, стягивает дугу в 60°.На расстоянии 15 см от плоскости трапеции находится точка, равноудаленная от всех вершин трапеции. Найдите расстояние от этой точки до вершин трапеции.

5. Дан двугранный угол величиной 30° и две прямые в его гранях, каждая из которых параллельна ребру двугранного угла. Эти прямые находятся на расстоянии 1 см и см от ребра. Докажите, что эти прямые принадлежат одной плоскости и найдите расстояние от ребра двугранного угла до нее.

6. Точка, лежащая вне плоскости прямого угла, удалена на расстояние 8 см от каждой из сторон этого угла. Найдите расстояние от данной точки до вершины этого угла, если точка удалена от плоскости на расстояние см.

7. В правильной четырехугольной пирамиде SABCD (S - ее вершина). Проведите сечение через середину ребра SC и прямую PК, расположенную в плоскости основания ABCD и параллельную его диагонали BD.

8. В АВС, где А(3; 0; - 4) и М (5; 4; - 3) - середина АВ, Р -середина АС. Найдите длину вектора, где N - середина ВС.

9. Вычислите площадь параллелограмма, построенного на векторах (8; 4; 1) и(2; - 2; 1).

10. Докажите, что треугольник с вершинами А (3; - 2; 1), В (- 2; 1; 3), С (1; 3; - 2) равносторонний.

11. Составьте уравнение сферы, которая: проходит через начало координат, а центр ее расположен в точке О (4; -4; 2);

12. Правильная шестиугольная призма, у которой боковые грани квадраты, пересечена плоскостью, проходящей через стороны нижнего основания и противолежащую ей сторону верхнего основания. Сторона основания равна 5 дм. Найти площадь полученного сечения.

13. В основании прямой призмы лежит ромб со стороной а. Диагонали призмы образуют с плоскостью основания углы и. Найдите объем призмы.

14. В правильной четырехугольной пирамиде плоский угол при вершине равен . Найдите объем пирамиды, если ее боковое ребро равноb.

15. В основании пирамиды лежит квадрат. Две боковые смежные грани пирамиды перпендикулярны к плоскости основания, а две другие наклонены к ней под углом . Определите объем пирамиды, если наибольшее боковое ребро равноl.

16. В правильной треугольной пирамиде плоский угол при вершине равен , а радиус окружности, описанной около боковой грани, равен R. Найдите объем пирамиды.

17. Основание пирамиды - трапеция, у которой параллельные стороны 30 см и 48 см, а высота 3 см. Длина каждого бокового ребра пирамиды 65 см. Найдите объем пирамиды.

18. В усеченном конусе, отношение площадей оснований которого равно 4, образующая длиной 4 см наклонена к плоскости основания под углом в 30°. Определить объем этого конуса.

19. Через две образующие конуса проведена плоскость, которая наклонена к плоскости основания под углом . Эта плоскость пересекает основание конуса по хорде, которую видно из центра его основания под углом. Найдите объем конуса, если его образующая равнаl.

20. В основании пирамиды лежит прямоугольный треугольник с углом . Все боковые ребра пирамиды наклонены к плоскости основания под углом. Найдите объем пирамиды, если радиус шара, описанного около нее, равен R.

21. В правильной четырехугольной пирамиде плоский угол при вершине равен . Определите полную поверхность конуса, описанного около пирамиды, если ее высота равна Н.