
200106_СДФ1_ПрИС
.pdf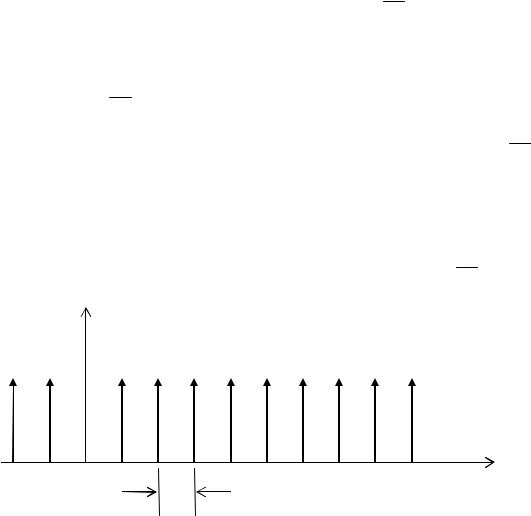
Амплитуда спектральных пиков |Cn| будет пропорциональна U. Устремим те-
перь t®0, а период T оставим без изменений. Поскольку 2tπ ® ¥ главный лепесток
спектра будет неограниченно расширяться и в пределе получим периодическую последовательность спектральных пиков с одинаковой амплитудой и периодом следо-
вания по частотной оси 2π .
T
В нашем случае T = D., поэтому шаг по частотной оси будет равен 2Dπ . Кроме
того, поскольку входной сигнал η(t) представляет собой последовательность дельтаимпульсов, U ~ d(t), следовательно, и |Cn| ~ d(t). В результате спектр Sη(w) также будет представлять собой бесконечную последовательность дельта-импульсов, но
уже в частотной области, с периодом следования по частотной оси 2Dπ .
S(w)
|
|
… |
0 |
2π |
w |
|
|
|
|
|
|
|
D |
|
Полученный спектр математически можно записать как
∞ |
|
2p |
|
|
Sη(ω)= ∑δ |
ω - |
|
n . |
|
D |
||||
n=−∞ |
|
|
Подставим Sη(ω) в формулу для спектра дискретного сигнала (*). Далее, из-
меняя порядок следования операций интегрирования и суммирования, и используя так называемое фильтрующее свойство дельта-функции (см. Баскаков С.И., п.1.2. Динамическое представление сигналов)
∞
∫ f (t) × δ(t0 - t) = f (t0 ) ,
−∞
получим искомый спектр

¥ |
|
|
2p |
|
|
|
S Д (ω) = ∑ S x |
ω - |
|
|
n |
||
D |
||||||
n=-¥ |
|
|
|
|
||
|
|
|
|
|
|
|
Таким образом, спектр дискретного сигнала, т.е. сигнала, полученного в результате дискретизации бесконечно короткими стробирующими импульсами, представляет собой сумму бесконечного числа «копий» спектра исходного аналогового сигнала. Копии располагаются на оси частот через одинаковые интервалы 2π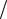 , равные значению частоты дискретизирующей импульсной
, равные значению частоты дискретизирующей импульсной
последовательности (частоты дискретизации wД):
ЛЕКЦИЯ 17
Дискретное преобразование Фурье.
Спектральные характеристики аналоговых сигналов определяются рядом Фурье (для периодических сигналов) или преобразованием Фурье (для непериодических сигналов). Рассмотрим ряд Фурье в его комплексном виде:
s(t ) = |
¥ |
jk |
2π |
×t |
|
|
||||||
|
|
|
||||||||||
∑ Ck × e |
|
|
T |
|
(***) |
|||||||
|
|
|
k =-¥ |
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
2 |
|
- jk |
2π |
×t |
|
|
||
|
|
|
|
|
|
|||||||
Ck |
= |
|
∫ |
s (t ) × e |
|
|
|
T |
dt |
(***) |
||
T |
|
|
|
|
|
|||||||
|
|
-T 2 |
|
|
|
|
|
|
|
|
||
Ряд Фурье предполагает, что сигнал полностью задан на конечном интервале [– T/2, T/2], или, что то же самое, [0, T]. Коэффициенты Ck представляют собой спектральное представление сигнала s(t). Рассмотрим теперь, как будут выглядеть формулы спектрального представления сигнала для дискретной цифровой последовательности. Для этого примем во внимание следующее:
1)поскольку цифровой сигнал в отличие от аналогового является не функцией, а последовательностью чисел (дискретных отсчётов), то в формуле для спектральных коэффициентов интегрирование должно быть заменено на суммирование;
2)любой цифровой сигнал на практике всегда задан не бесконечной, а конечной последовательностью N отсчётов, взятых на интервале времени от 0 до T. Таким образом, с формальной математической точки зрения мы можем разложить цифровой сигнал в ряд Фурье. При этом в формуле для спектральных коэффициентов суммирование должно производиться по N отсчетам, то есть от 0 до N – 1.

Исходя из этого, сразу запишем дискретное преобразование Фурье (ДПФ) для
цифровой последовательности N отсчётов (x0, x1, x2, … |
xN– 1): |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 N -1 |
|
|
|
- j |
2π |
×n×k |
|
|
||
|
Cn = |
|
|
× e |
|
– |
прямое ДПФ |
||||||
|
|
|
∑ xk |
|
|
N |
|||||||
|
|
|
N k =0 |
|
|
2π |
|
|
|
|
|
||
|
|
N -1 |
|
j |
×n×k |
|
|
||||||
|
|
|
|
|
|
||||||||
|
xk = |
|
∑ Cn |
× e |
|
N |
– |
обратное ДПФ |
|||||
|
|
n=0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные свойства ДПФ
1.ДПФ есть линейное преобразование, т.е. сумме сигналов соответствует сумма их ДПФ.
2.Число различных спектральных коэффициентов ДПФ равно числу времен-
ных отсчётов N : C0, C1, C2, … CN–1 . |
|
|
|
|
3. |
Коэффициент C0 является средним значением всех отсчётов: |
|||
|
|
|
1 |
N −1 |
|
C0 |
= |
|
∑ xk , |
|
|
|||
|
|
|
N k =0 |
|
– это постоянная составляющая цифрового (дискретного) сигнала. |
||||
4. |
Информацию о спектре |
несут только первые N / 2 значений: |
||
C1, C2 , |
... C N 2 . Вторая половина коэффициентов C N 2 +1,..., C N - 1 является ком- |
|||
плексным сопряжением коэффициентов первой половины. При этом комплексно сопряжённые пары располагаются симметрично относительно N/2:
С1 = С*N -1 ,
С2 = С*N -2 ,
…………
СN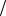 2-1 = C*N
2-1 = C*N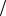 2+1,
2+1,
или в общем виде
C N -n = Cn*.
Таким образом, коэффициенты C N 2+1, ..., C N -1 образуют зеркальную копию коэффициентов C1, C2 , ... C N 2 , поэтому можно считать, что эти коэффициенты со-
ответствуют отрицательным частотам спектрального представления сигнала. Соответственно они не содержат в себе никакой новой информации, поскольку отри-
цательные частоты были введены в теорию сигналов только для удобства математических выкладок (см. курс ПрИС).
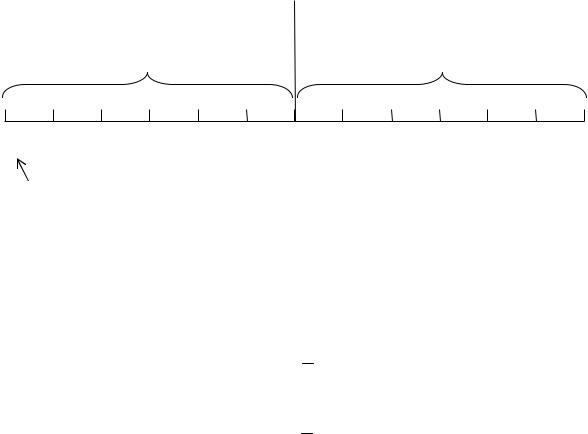
Графически распределение коэффициентов будет выглядеть следующим обра-
зом
основные спектральные |
зеркальная копия |
коэффициенты |
первой половины |
C0 C1 C2 |
CN/2– 1 CN/2 CN/2+1 |
CN– 2 CN– 1 |
постоянная составляющая
5. Если дискретная последовательность состоит всего из двух элементов x0 и x1, т.е. длина ряда N = 2, то коэффициенты ДПФ равны:
C0 = 1 (x0 + x1 )
2
С1 = 1 (x0 − x1 )
2
(эти формулы следуют из формулы (***) прямого ДПФ).
Соответствие числовых значений физических величин и номеров дискретных последовательностей. Частотно-временной анализ
Временное представление сигнала – это последовательность отсчетов { xk } = (x0 , x1 , x2 , …, xN – 1 ). Представим их графически
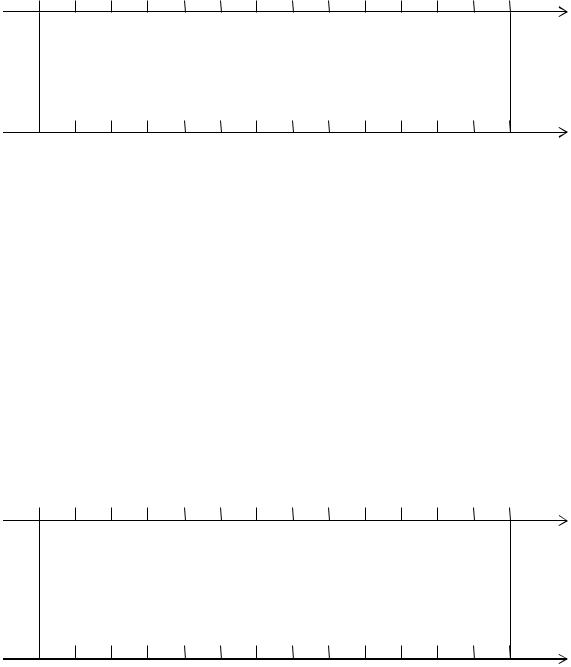
физическая временная ось
0 |
2 3 … |
T |
t
временная ось с разметкой в номерах отсчетов
0 |
|
1 |
2 |
3 |
… |
N–1 |
k |
|
где = |
1 |
– |
интервал дискретизации; T – |
длина интервала времени, на котором |
||||
f Д |
||||||||
|
|
|
|
|
|
|
||
задан исходный аналоговый сигнал, представленный N дискретными отсчётами. |
||||||||
Частотное |
представление сигнала – |
это спектральные |
коэффициенты |
|||||
{ Cn } = (C0 , |
C1 , |
C2 , …, |
CN / 2 ). Представим их графически |
|
||||
физическая частотная ось
0 |
f 2 f 3 f … |
fN |
t
частотная ось с разметкой в номерах коэффициентов ДПФ
0 1 2 3 … |
N / 2 |
k
Пояснения к частотному представлению.
Количество независимых коэффициентов ДПФ равно, по определению, N/2. fN – частота Найквиста, которая по определению является верхней границей частотного интервала спектра ДПФ, равна

fN |
= |
f |
Д |
= |
1 |
. |
|
|
|
|
|||||
2 |
2D |
||||||
|
|
|
|
||||
Df – частотный дискрет, то есть шаг следования коэффициентов ДПФ по частотной оси, определяется из равенства
|
|
f N |
= Df × |
N |
|
|
|
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
||
Таким образом, частотный дискрет Df будет равен |
|
|||||||||||
Df = |
f N |
|
= |
|
1 |
× |
2 |
|
= |
1 |
. |
|
|
|
|
2D |
N |
N × D |
|||||||
|
N 2 |
|
|
|
|
|||||||
Проектирование и реализация цифровых фильтров
Пара преобразования ДПФ и ОДПФ позволяет осуществлять цифровую фильтрацию. Отметим основные моменты такого способа цифровой фильтрации:
1. ДПФ означает переход от временных дискретных отсчетов (x0, …, xN–1 ) к совокупности частотных дискретных значений (С0, …, СN/2). При этом спектральные коэффициенты содержат полностью всю информацию, которая содержится в дискретной последовательности {xk}. Это позволяет осуществить обратный переход от коэффициентов {Сn} с помощью ОДПФ к отсчетам {xk}, и далее восстановить, при условии выполнения теоремы Котельникова, исходный аналоговый сигнал.
2. Основной характеристикой системы, которая осуществляет фильтрации сигнала, является его АЧХ и ФЧХ. Вид АЧХ определяет вид фильтрации: ФНЧ, ФВЧ, ПФ, режекторный (заградительный) фильтры. Коэффициенты {Сn} имеют смысл вклада в сигнал различных спектральных составляющих – от нижних частот к высоким. Если эти коэффициенты умножить на некоторую весовую функцию, имеющую вид конкретной избирательной АЧХ, то тем самым, после ОДПФ, мы осуществим фильтрацию сигнала.
Соответственно сказанному, последовательность преобразований при цифровой фильтрации методом ДПФ можно представить следущей схемой:
sвх(t) |
|
|
|
|
|
|
|
|
|
sвых(t) |
||
|
АЦП |
|
ДПФ |
|
ЦФ |
|
ОДПФ |
|
ЦАП |
|
Ф |
|
|
|
|
|
|
|
|
||||||
|
|
(БПФ) |
|
|
(ОБПФ) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
На практике все блоки данной схемы (за исключением аналогового фильтра Ф) можно реализовать на одной интегральной схеме (ИС) специализированного микропроцессора, так называемого цифрового сигнального процессора (DSP, – digital signal proccessor). Эти микропроцессоры имеют как правило встроенные АЦП/ЦАП, память программ и данных, разрядность 16 или 32 бита, что позволяет проводить необходимые числовые вычисления.
Подобную цифровую фильтрацию можно осуществить, разумеется, и с помощью компьютера, если он входит в состав системы ЦОС.
ЦФ методом ДПФ проста для понимания, но имеет несколько существенных недостатков, смысл которых станет яснее после рассмотрения других способов ЦФ. Отметим здесь пока два из них: данный способ ЦФ, даже при использовании вместо ДПФ алгоритма БПФ, требует неоправданного большого числа вычислений. Кроме того, задержка, вносимая ЦФ при получении выходного сигнала, также оказывается слишком большой. Существует более экономичные способы ЦФ, которые, в свою очередь, делятся на два типа: рекурсивные и нерекурсивные ЦФ.
Лабораторная работа № 1
ПОСТРОЕНИЕ ГРАФИКОВ МОДЕЛЬНЫХ ФУНКЦИЙ НА ЭКРАНЕ МОНИТОРА КОМПЬЮТЕРА
Цель работы
Целью работы является овладение навыками графического представления (визуализации) на экране монитора модельных математических функций и экспериментальных данных с помощью средств, предоставляемых алгоритмическим языком Бейсик с последующим электронным документированием готовых графических изображений и вставкой их в виде иллюстраций в документ текстового процессора MS Word. Все приведенные задания можно также выполнить с использованием визуального языка программирования Visual Basic.
Задание 1
Построение графиков функций с помощью оператора PSET (x,y)
1.1. Запустите интерпретатор QBasic. Задайте графический режим SCREEN 12. Этим оператором экран монитора переводится в графический режим. В этом режиме изображение выводится по точкам экрана (пикселам).
Положение точки на экране задается двумя параметрами: x и y (задающие экранную систему координат). Начало координат этой экранной системы координат (x = 0, y = 0) расположено в левом верхнем углу экрана, поэтому ось y направлена вниз, а не вверх (рис. 1.1). Это необходимо иметь ввиду при построении графиков.
Для вывода графической информации используются графические операторы PSET и LINE. Синтаксис этих операторов следующий:
PSET (x, y) – графический оператор, рисующий точку на экране с координатами x и y. Например, оператор PSET (100, 100) высветит точку на экране с координатами x=100 и y=100 (как показано на рис. 1.1)
LINE (x1, y1) – (x2, y2), цвет линии – |
рисование линии. Параметры x1, y1 оп- |
ределяют координаты начала линии, x2, |
y2 – координаты конца линии. Необяза- |
тельный параметр – цвет линии – задает цвет выводимой линии (номер цвета задается числом от 0 до 15).
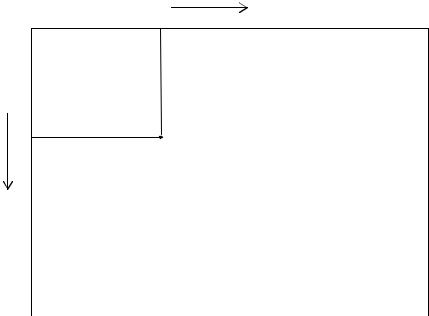
|
x |
0,0 |
640, 0 |
|
(100,100)
y
0, 480 |
|
640, 480 |
|
Рис. 1.1. Экранная система координат
1.2. Постройте график функции y = sin x в диапазоне x от 0 до 360° с помощью оператора PSET (x, y). В программе в цикле вычисления функции перед вычислением функции переведите значения аргумента x из градусов в радианы. Это лучше сделать отдельным оператором с использованием вспомогательной переменной, например, xr.
SCREEN 12
CLS
pi = 3.14
FOR x = 1 TO 360 STEP 1 xr = x * pi /180
y = SIN ( xr )
PSET ( x, 200 – y * 50 ) NEXT x
В этой программе аргумент x (значения от 0 до 360) без преобразования принимается как экранная координата x (всего на экране в режиме SCREEN 12 умещается 640 точек по горизонтали и 480 точек по вертикали – см. описание графических режимов в справке QBasic; справочная информация вызывается по нажатию клави-
ши <F1>). Для значений функции y уже используется преобразование: изменение знака, масштабирование (умножение на 50) и смещение (на 200 точек вниз).
1.3.С помощью двух операторов LINE постройте две координатные оси: ось x
иось y.
1.4.Сохраните программу под номером 1.
Задание 2
Построение графика функции с помощью оператора LINE – (x,y). Построение двух кривых на одном графике
2.1. Постройте график функции y = sin x (см. Программу 1) с добавлением случайного шума (моделирование погрешности измерений). Значения шума смоделируйте с помощью встроенного генератора равномерно распределенных случайных чисел RND. Например,
y = SIN(xr) + RND – 0.5
2.2.Постройте график функции не отдельными точками с помощью оператора PSET (x, y), а сегментированными линиями с помощью оператора LINE – (x, y). Убедитесь, что таким образом устраняются разрывы линии при рисовании кривой графика. Перед началом цикла рисования необходимо поместить курсор в точку начала координат. Это можно сделать оператором PSET (Xs, Ys), где Xs, Ys – смещения графика в пикселах экрана (для программы п 1.2. эти смещения равны соответственно 0 и 200).
2.3.Постройте на одном графике две кривые – функцию y = sin x и ту же функцию с шумом. Выделите две кривые разным цветом.
2.4.Сохраните программу под номером 2.
Задание 3
Построение графика функции в графическом окне. Операторы VIEW и WINDOW
Оператор VIEW выделяет на экране монитора прямоугольную область («окно»), которое становится по сути новым экраном, доступным для работы. С момента объявления «окна», все графические операторы будут относится к этому «окну». Синтаксис оператора следующий
VIEW (x1, y1) – (x2, y2)
