Обобщенные силы и способы их вычисления

Рассмотрим механическую систему с идеальными связями. Пусть  активные силы системы. Дадим механической системе виртуальное перемещение и вычислим элементарную работу сил системы на этом перемещении:

.

Используя равенство (17.2) выразим вариацию радиусавектора точкиM_k через вариации обобщенных координат:

и,

следовательно,

. (17.6)

Поменяем в равенстве (17.6) порядок суммирования:

. (17.7)

Обозначим в выражении (17.7)

. (17.8)

Получим

.

Обобщенными силами Q_j называют коэффициенты при вариациях обобщенных координат в выражении элементарной работы сил системы.

В зависимости от размерности вариаций обобщенных координат обобщенные силыQ_j могут иметь размерность силы, момента и др.

Способы вычисления обобщенных сил

Рассмотрим три способа вычисления обобщенных сил.

1. Определение обобщенных сил по основной формуле (17.8)

. (17.9)

Формула (17.9) на практике применяется редко. При решении задач чаще применяется второй способ.

2. Способ «замораживания» обобщенных координат.

Дадим механической системе такое виртуальное перемещение, при котором все вариации обобщенных координат кроме равны нулю:

.

Вычислим на это перемещение работу всех активных сил, приложенных к системе

.

По определению множитель при вариации равен первой обобщенной силеQ₁.

Далее дадим системе виртуальное перемещение

и определим вторую обобщенную силу Q₂, вычислив виртуальную работу всех сил системы

.

Аналогично вычислим все остальные обобщенные силы системы.

3. Случай потенциального силового поля.

Предположим, известна потенциальная энергия механической системы

.

Тогда и по формуле (32.8)

. (17.10)

Принцип виртуальных перемещений статики в обобщенных координатах

Согласно принципу виртуальных перемещений статики для равновесия системы с идеальными удерживающими голономными, стационарными связями необходимо и достаточно является условие

при нулевых начальных скоростях.

Переходя к обобщенным координатам, получим

. (17.11)

Так как вариации обобщенных координат независимы, то равенство нулю выражения (17.11) возможно только в том случае, когда все коэффициенты при вариациях обобщенных координат равны нулю:

. (17.12)

Таким образом, для того, чтобы механическая система с идеальными, голономными, стационарными и удерживающими связями находилась в равновесии необходимо и достаточно, чтобы все обобщенные силы системы равнялись нулю (при нулевых начальных скоростях системы).

Уравнения Лагранжа в обобщенных координатах (уравнения Лагранжа второго рода)

Уравнения Лагранжа выводятся из общего уравнения динамики заменой виртуальных перемещений их выражениями через вариации обобщенных координат. Они представляют собой систему дифференциальных уравнений движения механической системы в обобщенных координатах:

. (17.13)

где  обобщенные скорости,

Т  кинетическая энергия системы, представленная как функция обобщенных координат и обобщенных скоростей

,

Q_j  обобщенные силы.

Число уравнений системы (17.13) определяется числом степеней свободы и не зависит от количества тел входящих в систему. При идеальных связях в правые части уравнений войдут только активные силы. Если связи неидеальны, то их реакции следует отнести к активным силам.

В случае потенциальных сил, действующих на механическую систему уравнения (17.13) примут вид

.

Если ввести функцию Лагранжа L = Т  П, то учитывая, что потенциальная энергия не зависит от обобщенных скоростей, получим уравнения Лагранжа второго рода для случая потенциальных сил в следующей форме

.

При составлении уравнений Лагранжа второго рода нужно выполнить следующие действия:

1. Установить число степеней свободы механической системы и выбрать ее обобщенные координаты.

2. Составить выражение кинетической энергии системы и представить ее как функцию обобщенных координат и обобщенных скоростей.

3. Пользуясь изложенными выше способами найти обобщенные активные силы системы.

4. Выполнить все необходимые в уравнениях Лагранжа операции дифференцирования.

Пример.

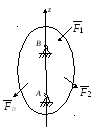
Рис.17.3

Составим дифференциальное уравнение вращательного движения твердого тела, находящегося под действием системы активных сил (рис.17.3) по выше изложенному алгоритму. 1. Тело, совершающее вращательное движение имеет одну степень свободы. За обобщенную координату примем угол : q = . 2. Кинетическая энергия тела при вращении вокруг неподвижной оси равна ,

где J_z  момент инерции тела относительно оси вращения z,  угловая скорость тела.

3. Определим обобщенную силу. Дадим телу виртуальное перемещение  и вычислим виртуальную работу всех активных сил системы:

.

Следовательно, Q = M_z  главный момент активных сил системы относительно оси вращения тела.

4. Выполним операции дифференцирования в уравнении Лагранжа

: (17.14)

. (17.15)

Подставляя равенства (17.15) в уравнение (173

.14) получим дифференциальное уравнение вращательного движения тела

.