FTF 2 semestr.MARTINOV / 25

Тензор называется симметричным по двум индексам i и j, если он не меняется при перестановке этих индексов:

Если тензор не меняется при перестановке любой пары своих индексов, то такой тензор называется абсолютно симметричным.

Симметризация и антисимметризация

Для любого тензора U, с компонентами , можно построить симметричный и антисимметричный тензор по правилу:

 (симметричная часть),

 (антисимметричная часть).

Термин «часть» означает, что 

Для большего числа индексов тоже можно определить симметризацию:

,

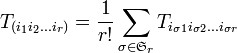обозначаемую также (для случая её проведения по всем индексам) символом :

.

Однако, для разложения тензора ранга, большего двух, оказывается недостаточно лишь абсолютно симметричного и абсолютно антисимметричного слагаемых.

Примеры абсолютно симметричных тензоров

• Ранга 0 — скаляр (любой),

• Ранга 1 — вектор/ковектор (любой),

• Ранга 2:

  • симметричная матрица,

  • (ковариантный) — квадратичная форма.

Тензорный эллипсоид.

С каждым вектором   можно сопоставить семейство перпендикулярных ему плоскостей, описываемых уравнением           

 (  ^.  ) = const          (1.92)

Подобно этому, симметричным тензором второго ранга   можно сопоставить семейство поверхностей второго порядка. Уравнение одной из них

   ^.  .  =1           (1.92)', или

 Т₁₁ x²₁+ Т₂₂ x²₂+ Т₃₃ x²₃+ 2Т₁₂ x₁ x₂+ 2Т₂₃ x₂ x₃+2Т₃₁ x₁ x₃=1                      (1.92)''

Если главные значения тензора   - числа положительные (именно этот случай представляет больший интерес для физики), то (1.92)'' – уравнение трехосного эллипсоида, который принято называть тензорным эллипсоидом.

Чтобы убедиться в этом, достаточно перейти к системе координат, оси которой совпадают с главными осями тензора. В ней тензор имеет вид 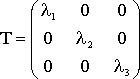а уравнение (1.92)''    

   ₁x²₁+  ₂x²₂+  ₃x²₃=1                 (1.92)'''

Это – уравнение трехосного эллипсоида, оси которого совпадают с осями тензора, а длины полуосей равны (  ₁)^-1/2, (  ₂)^-1/2, (  ₃)^-1/2.