FTF 1 semestr.MAVRODI / 80
.pdf
признак сходимости Абеля(интегралы 1го рода): |
|
|
1. пусть функции f(x) и g(x) определены в промежутке |
, |
|
причём f(x) интегрируема в этом промежутке, т.е. интеграл |
сходится |
|
(условно или абсолютно); |
|
|
2. g(x) монотонна и ограничена: |
. |
|
Тогда интеграл |
сходится. |
|
Признак Абеля(интегралы 2го рода). Интеграл |
сходится, |
если: |
|
1).функция f(x) непрерывна на (a, b] и интеграл |
сходится; |
2).функция g(x) ограничена, непрерывно дифференцируема и монотонна на (a, b], то есть имеет конечный предел:
.
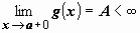Признак Абеля сходимости несобственных интегралов
Признак Абеля дает достаточные условия сходимости несобственного интеграла.
Признак Абеля для несобственного интеграла I-рода (для бесконечного промежутка). Пусть функции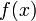 
и 
определены на промежутке 
. Тогда несобственный
интеграл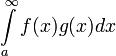 
сходится, если выполнены следующие условия:
1.Функция 
интегрируема на 
.
2.Функция 
ограничена и монотонна.
Признак Абеля для несобственного интеграла II-рода (для функций с конечным числом разрывов).
Пусть функции 
и 
определены на промежутке 
. Тогда несобственный
интеграл |
сходится если выполнены следующие условия: |
1.Функция 
интегрируема на 
т.е. сходится интеграл
2.Функция 
ограничена и монотонна на 
.