
- •1986 Сканирование:
- •Содержание
- •Возвращение риторики
- •От авторов
- •I. Общая теория фигур
- •1. Членение дискурса
- •1.1. Значимые единицы языка
- •1.2. Описание областей
- •2. Исходные понятия
- •2.1. Нулевая ступень
- •2.2. Автокоррекция и избыточность
- •2.3. Отклонение и конвенция
- •2.4. Инвариант
- •2.5. Выводы
- •3. Риторические операции
- •3.1. Субстанциальные операции
- •3.2. Реляционные операции
- •3.3. Графики и таблицы
- •89 Общая таблица метабол, или риторических фигур
- •II. Метаплазмы
- •0. Общие замечания
- •0.1. Фонетическое слово
- •0.2. Метаплазмы и метаграфы
- •0.3. Уровни
- •1. Сокращение
- •2. Добавление
- •3. Сокращение с добавлением
- •4. Перестановка
- •5. Частные проблемы
- •5.1. Метаплазмы и литература
- •5.2. Арго
- •5.3. Метаграфы
- •III. Метатаксис
- •0. Общие замечания
- •1. Сокращение
- •2. Добавление
- •3. Сокращение с добавлением
- •4. Перестановка
- •5. Прикладное исследование: метатаксис в заголовках периодической печати
- •IV. Метасемемы
- •0.1. Общие замечания
- •0.2. Определения
- •0.3. Виды декомпозиции
- •0.4. Минимальное отклонение
- •0.5. Избыточность и редукция
- •0.6. Несколько моделей представления семантической информации
- •0.7. Конкретное и абстрактное
- •1. Синекдоха*
- •1.3. Сохранение главных сем
- •2. Метафора
- •2.1. Семантическая несовместимость
- •2.2. Пересечение и объединение
- •2.3. Соположение синекдох
- •2.4. Скорректированные метафоры
- •2.5. Метафоры in praesentia и метафоры in absentia
- •3. Сравнения
- •3.1. Различные виды сравнений
- •3.2. Грамматические связки
- •4. Метонимия
- •4.1. Смежность
- •4.2. Коннотация
- •5. Оксюморон
- •6. Наложение — антиметабола — — антанаклаза
- •V. Металогизмы
- •0. Общие замечания
- •0.1. Метасемемы и металогизмы
- •0.2. Традиционная риторика и общая риторика
- •0.3. Логика и металогизмы
- •0.4. Металогизмы и фигуры мысли
- •0.5. Протяженность металогизмов
- •0.6. Выделение элементов металогизма
- •1. Сокращение
- •2. Добавление
- •3. Сокращение с добавлением
- •4. Перестановка
- •VI. На подступах к изучению явления этоса
- •0. Общие замечания
- •1. Ядерный этос
- •1.1. Риторическая функция и неспецифический характер метабол
- •1.2. Вариативность ядерного этоса
- •2. Автономный этос
- •3. Контекстуальный этос
- •4. Этос и суждение
- •Предварительные замечания
- •I. Фигуры, связанные с отправителем и получателем сообщения
- •0. Общие замечания
- •1. Коммутация «лицо/не-лицо»
- •2. Коммутация по признаку «соотнесенность/несоотнесенность с участниками акта коммуникации»
- •3. Коммутация по признаку «отправитель/получатель сообщения»
- •4. Коммутация «определенность/неопределенность»
- •5. Коммутация «единственное число/множественное число»
- •6. Дополнительные замечания
- •7. Выводы
- •II. Фигуры повествования
- •0. Общие замечания
- •1. Фигуры субстанции выражения
- •1.1. Суппорт (материя) и субстанция
- •1.2. Нормы и отклонения
- •1.3. Дистрибуция и интеграции
- •2. Фигуры формы выражения: повествовательный дискурс
- •2.0. Общие замечания
- •2.1. Соотношение длительностей
- •2.2. Факты и хронология
- •2.3. Последовательности фактов и причинный детерминизм
- •2.4. Представление пространства в дискурсе
- •2.5. Точка зрения
- •3. Фигуры формы содержания: повествование
- •3.0. Общие замечания
- •3.1. Ядра
- •3.2. Персонажи и индексы
- •3.3. Информанты
- •3.4. Актанты и отношение персонажей к актантам
3.2. Реляционные операции
Такие операции проще по своей структуре, поскольку их действие сводится к изменениям линейного порядка значимых единиц, в то время как сами эти единицы не претерпевают каких бы то ни было изменений. Здесь речь идет только о перестановках (permutations), среди которых можно выделить обычные и инвертированные. В последнем случае единицы звуковой или графической последовательности выстраиваются в обратном порядке.
3.3. Графики и таблицы
В таблице VI представлены все те операции, о которых мы говорили выше. Они реализуют все возможности рассматриваемой системы. В этой таблице отражена также совместимость этих операций с тремя группами фигур, которые были описаны выше (раздел 1.1). В частности, из таблицы явствует, что операция отрицания фонемы, графемы, синтаксической конструкции и т. д. лишена всякого смысла, так же как и, впрочем, повтор семы в пределах одной лексемы. Что касается перестановки сем в лексеме, то данная операция невозможна, поскольку этим составляющим присуща иерархическая, а не линейная упорядоченность. По той же причине невозможна перестановка различительных признаков внутри фонемы. Возможность перестановки на уровне предложений вызывает у нас сомнения, хотя гипотеза о существовании логической упорядоченности предложений дает основания предполагать, что такая перестановка в принципе возможна. Что
87
касается одновременной подмены всех синтаксических констант, то эта операция, как нам кажется, должна быть исключена из рассмотрения.
Проведем прямую с начальной точкой О и отметим на ней число дискретных единиц начиная с О и (по крайней мере теоретически) до бесконечности. Здесь учитывается только количество единиц (индексы m и n), но не их качество. На этом графике любой значимой единице U соответствует точка на прямой:
![]()
Рис. 3
Таблица VI
Операции и области их применения
|
Класс |
A |
BиC | |||
|
Членение |
Инфраязыковые единицы (различительные признаки) |
Языковые единицы и единицы более высокого уровня | |||
|
|
Означающее
|
Означаемое |
Означающее |
Означаемое | |
|
Сокращение
|
частичное полное
|
+ + |
+ +
|
+ + |
+ + |
|
Добавление
|
простое итеративное**
|
+ – |
+ – |
+ + |
+ + |
|
Сокращение с добавлением
|
частичное полное отрицающее*
|
+ + – |
+ + + |
+ + – |
+ + + |
|
Перестановка
|
обычная инвертированная**
|
– – |
– – |
+ + |
+ + |
+ = возможно
– = невозможно
* = всегда противопоставляет означающее и означаемое
** = противопоставляет А/В и С, то есть инфраязыковой уровень «всем остальным».
88
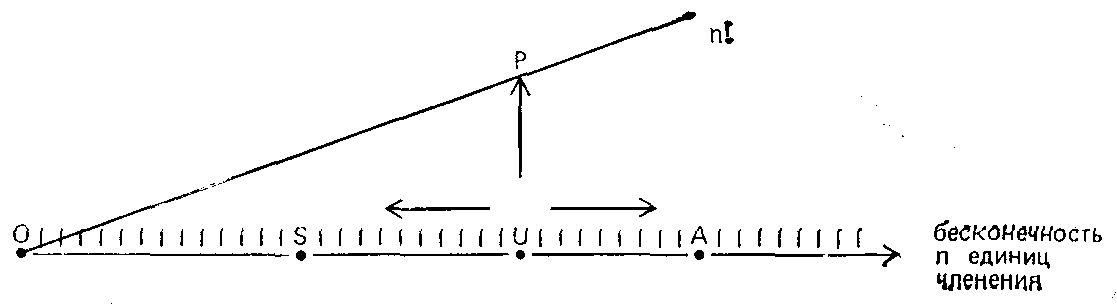
Рис. 4
Положение точки U на прямой будет определяться числом единиц членения n, на которые может быть разложена значимая единица U. Тогда операции А и S могут быть обозначены на прямой точками, лежащими в случае добавления справа, а в случае сокращения — слева от U.
Реляционные операции (перестановки) не влияют на число составляющих значимой единицы: следовательно, они не могут быть представлены на оси, изображенной на рис. 3. Они расположены вертикально относительно оси субстанциальных операций, то есть они не зависят от нее.
Дополняя наше графическое изображение, мы расположим перестановки на прямой, перпендикулярной бесконечной прямой О; полученная система координат будет чем-то напоминать графическое представление комплексных чисел в алгебре. Теоретически возможное число перестановок зависит от числа единиц членения (например, от числа букв в слове, числа слов во фразе) : оно равно n! = n(n — 1) (n — 2) ...3.2.1. Область перестановок Р (permutations) будет, таким образом, ограничена кривой n!, и теперь мы можем получить полное графическое изображение двумерного риторического пространства. Было бы ошибочным считать, что такому изображению нельзя сопоставить содержательную интерпретацию, напротив, на нем прекрасно видно, как «расширяется» пространство по мере того, как растет величина n: чем большее количество единиц получается в результате членения данной значимой единицы, тем большие возможности предоставляет она для риторической обработки.
