
Elektrodinamika / ЛР №7
.docЛАБОРАТОРНАЯ РАБОТА №…
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
ОСНОВНЫЕ ФОРМУЛЫ
Формулы преобразования Лоренца для составляющих электромагнитного поля в произвольной материальной среде:
![]() ,
,
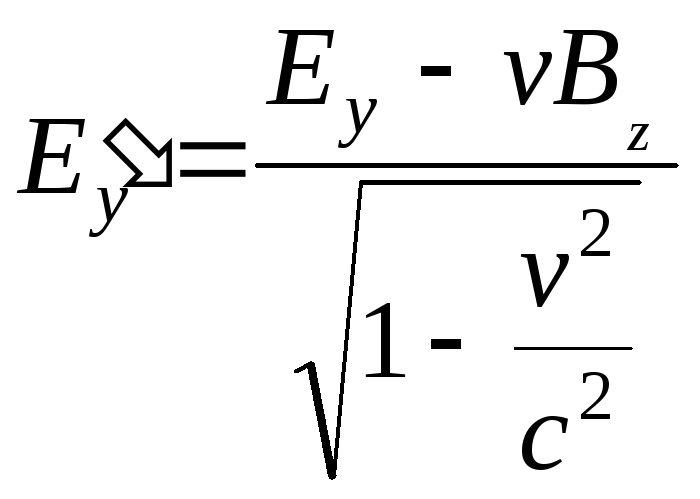 ,
,
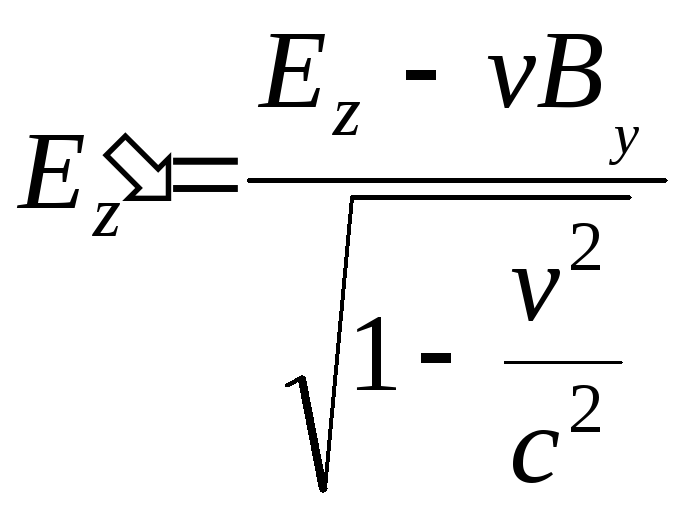 ,
(1)
,
(1)
![]() ,
,
 ,
,
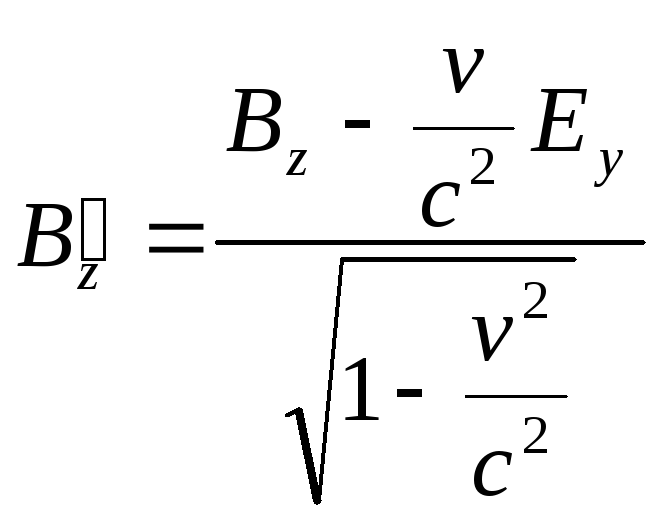 ,
(2)
,
(2)
или
![]() ,
,
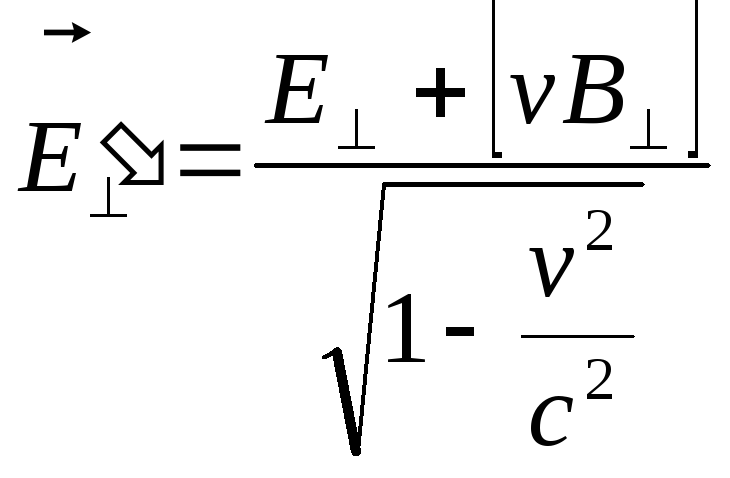 ,
(3)
,
(3)
![]() ,
,
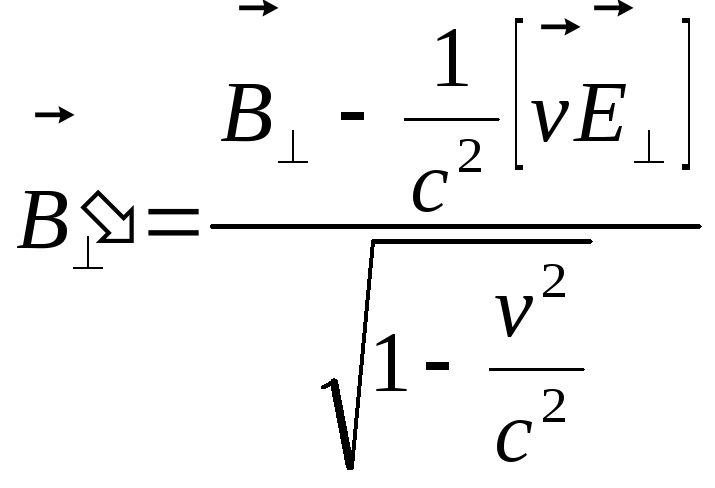 ,
(4)
,
(4)
где
![]() – скорость системы отсчета К'
относительно системы К;
– скорость системы отсчета К'
относительно системы К;
![]() ,
,
![]() – составляющие поля, параллельные
скорости
– составляющие поля, параллельные
скорости
![]() и
и
![]() ,
,
![]() – составляющие поля, перпендикулярные
к скорости
– составляющие поля, перпендикулярные
к скорости
![]() .
.
Формулы преобразования
Лоренца для составляющих векторов
![]() можно получить из формул (3) и (4),
воспользовавшись соотношениями
можно получить из формул (3) и (4),
воспользовавшись соотношениями
![]() и
и
![]() ,
при этом следует помнить, что при переходе
от одной инерциальной системы отсчета
к другой вектор
,
при этом следует помнить, что при переходе
от одной инерциальной системы отсчета
к другой вектор
![]() преобразуется через вектор
преобразуется через вектор
![]() ,
а вектор
,
а вектор
![]() – через вектор
– через вектор
![]() .
В результате находим следующие формулы
преобразования Лоренца для векторов
.
В результате находим следующие формулы
преобразования Лоренца для векторов
![]() :
:
![]() ,
,
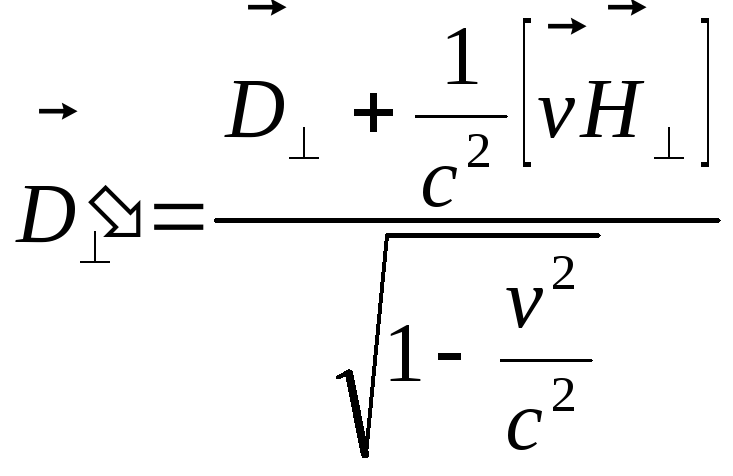 ,
(5)
,
(5)
![]() ,
,
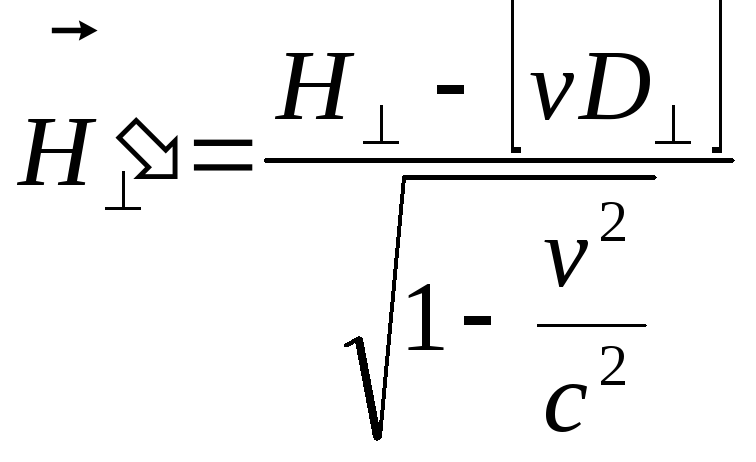 ,
(6)
,
(6)
![]() ,
,
 ,
(7)
,
(7)
![]() ,
,
 ,
(8)
,
(8)
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
Определить
электромагнитное поле точечного заряда
е,
движущегося в вакууме с постоянной
скоростью
![]() близкой к скорости света с.
близкой к скорости света с.
Решение
В собственной системе отсчета К', т.е. в системе, относительно которой заряд покоится, электрическое поле точечного заряда определяется формулами:
![]() ,
,
![]() ,
,
![]() ,
,
а магнитное поле отсутствует.
В лабораторной системе отсчета К по формулам преобразования Лоренца (1), (2) находим:
![]() ,
,
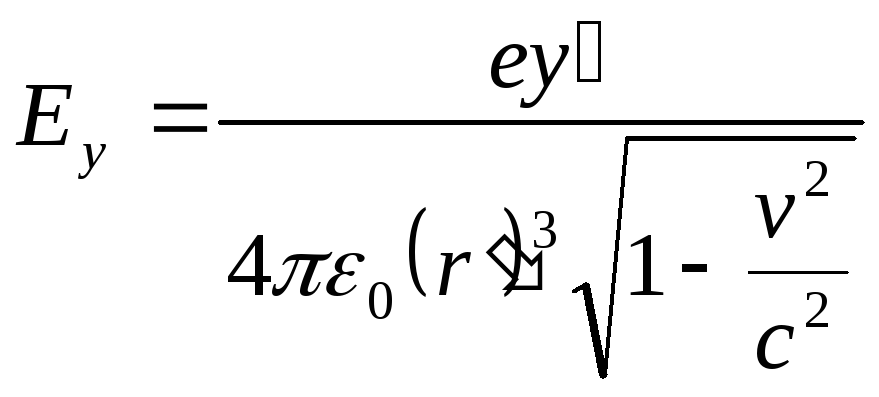 ,
,
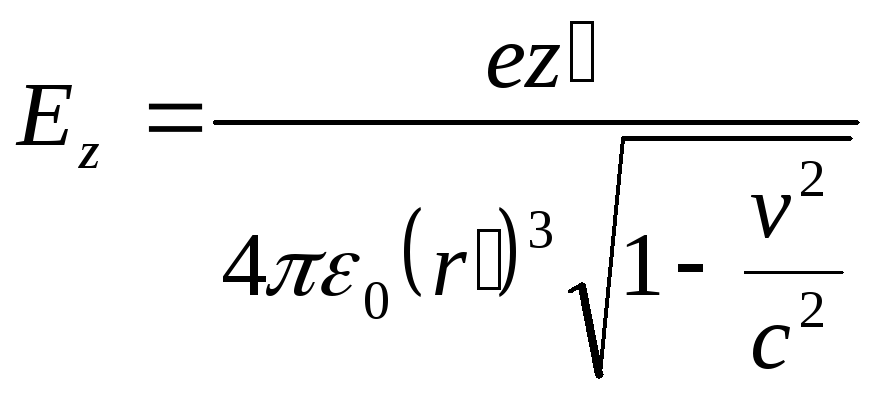
![]() ,
,
 ,
,
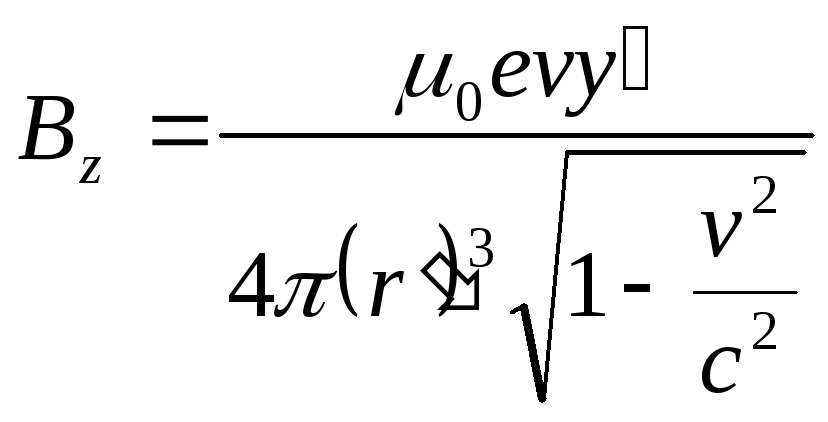
Здесь
![]() .
.
Подставляя в
![]() выражения для
выражения для
![]() ,
,
![]() и
и
![]() ,
записанные через нештрихованные
величины, определяемые из формул
преобразования Лоренца для четырехмерного
радиус-вектора, т.е.
,
записанные через нештрихованные
величины, определяемые из формул
преобразования Лоренца для четырехмерного
радиус-вектора, т.е.
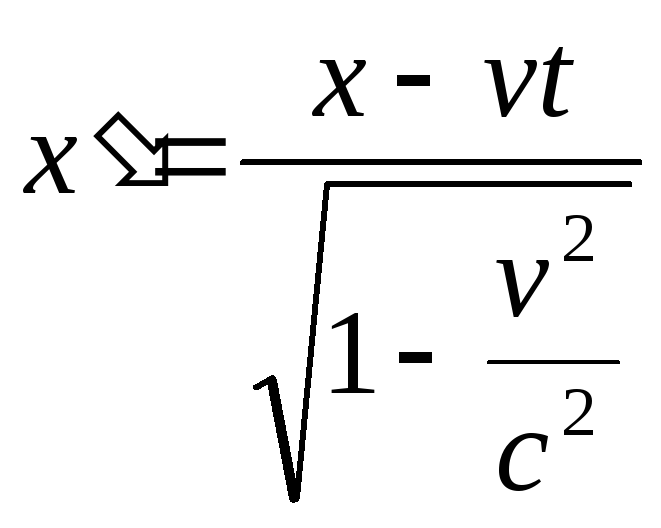 ,
,
![]() ,
,
![]() ,
,
получим:
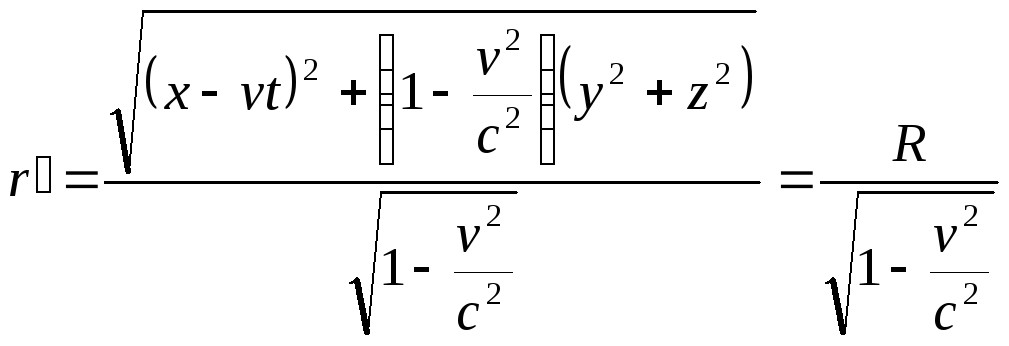 ,
(1)
,
(1)
где введено обозначение
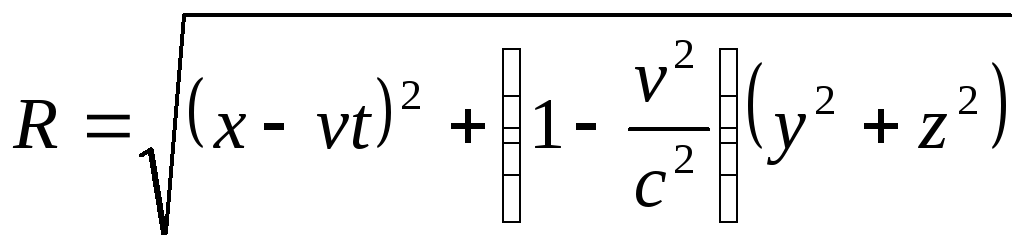 .
.
Используя выражение (1), составляющие напряженности электрического поля заряда в лабораторной системе отсчета К можно представить в виде:
![]() ,
,
![]() ,
,
![]()
или в векторной форме
![]() ,
,
где
![]() .
.
Составляющие вектора индукции магнитного поля движущегося заряда можно представить в виде:
![]() ,
,
![]() ,
,
![]()
или в векторной форме
![]() .
.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. В лабораторной
системе отсчета K
электрическое и магнитное поля направлены
под углом
![]() друг к другу. Определить скорость
движущейся перпендикулярно к обоим
полям системы отсчета
друг к другу. Определить скорость
движущейся перпендикулярно к обоим
полям системы отсчета
![]() в которой электрическое и магнитное
поля оказываются между собой параллельными.
в которой электрическое и магнитное
поля оказываются между собой параллельными.
2. Частица, заряд
которой равен е,
а масса покоя – m,
влетает с начальной скоростью
![]() в однородное и постоянное электрическое
поле Е,
перпендикулярное к
в однородное и постоянное электрическое
поле Е,
перпендикулярное к
![]() .
Найти траекторию частицы и показать,
что при
.
Найти траекторию частицы и показать,
что при
![]() она принимает вид параболы.
она принимает вид параболы.
3. Электрон влетает
в однородное и постоянное магнитное
поле с начальной скоростью
![]() ,
перпендикулярной к направлению поля.
Найти траекторию электрона.
,
перпендикулярной к направлению поля.
Найти траекторию электрона.
4. Определить угол
отклонения релятивистской
![]() -частицы,
пролетающей в поле ядра с зарядом Ze.
-частицы,
пролетающей в поле ядра с зарядом Ze.
 5.
Вычислить интенсивность дипольно
электрического излучения релятивистской
заряженной частицы, движущейся в
однородном и постоянном электрическом
поле
5.
Вычислить интенсивность дипольно
электрического излучения релятивистской
заряженной частицы, движущейся в
однородном и постоянном электрическом
поле
![]() ,
перпендикулярном к направлению ее
начальной скорости
,
перпендикулярном к направлению ее
начальной скорости
![]() .
.
6. Определить разность потенциалов на стенках однородной, намагниченной ленты (прямоугольного сечения), движущейся со скоростью, малой по сравнению со скоростью света (рис. 1).
7. В среде, движущейся со скоростью v относительно некоторой системы K, распространяется плоская электромагнитная волна. Найти скорость распространения волны в системе K, если показатель преломления среды равен n.
8. Найти траекторию
движения заряженной частицы в однородном
электрическом поле с напряженностью
![]() .
Рассмотреть предельный случай малых
скоростей.
.
Рассмотреть предельный случай малых
скоростей.
9. Найти систему отсчета, в которой электрическое и магнитное поля параллельны.
