Elektrodinamika / ЛР №5

ЛАБОРАТОРНАЯ РАБОТА №5

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

ОСНОВНЫЕ ФОРМУЛЫ

Полная система уравнений Максвелла для переменного электромагнитного поля:

, (1)

, (2)

, (3)

. (4)

Плотность энергии электромагнитного поля:

. (5)

Плотность потока электромагнитной энергии (вектор Пойнтинга):

. (6)

Плотность электромагнитного импульса:

. (7)

Обобщенные (запаздывающие) электродинамические потенциалы:

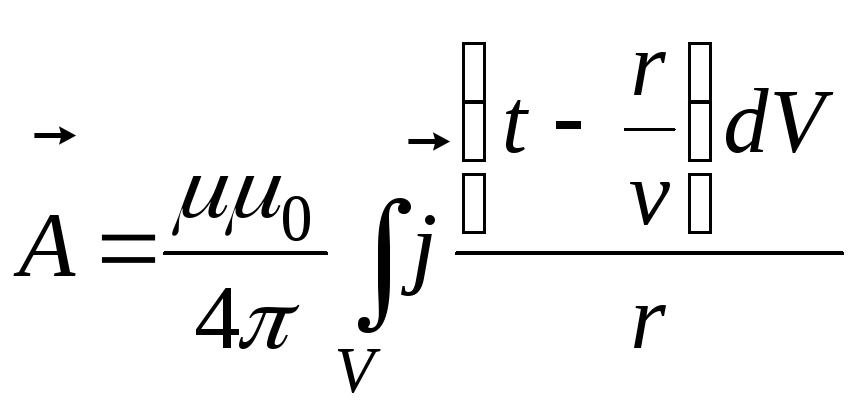, (8)

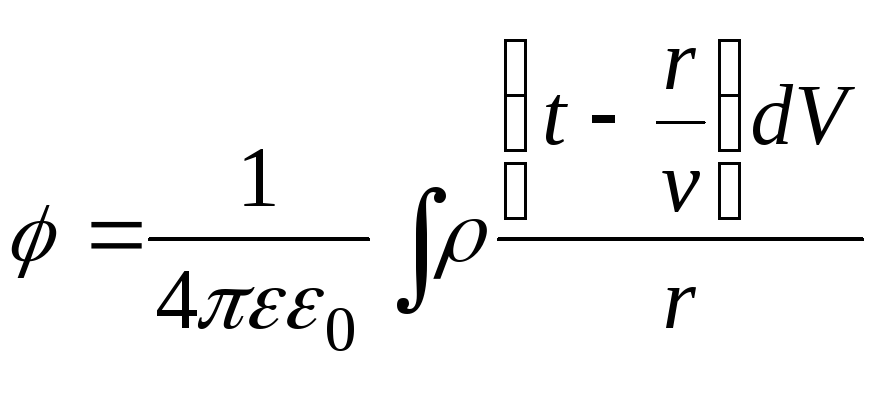. (9)

Связь векторов и с электромагнитными потенциалами:

, (10)

. (11)

Для однородных изотропных сред электромагнитные потенциалы и определяются из следующих уравнений Даламбера:

, (12)

. (13)

При этом потенциалы и предполагаются калиброванными по Лоренцу, т.е.

. (14)

Уравнения (12) и (13) при описывают свободные электромагнитные волны, распространяющиеся с фазовой скоростью:

, (15)

где с – скорость света в вакууме; n – показатель преломления.

В случае однородной среды из (1)–(4) также можно получить уравнения второго порядка для и :

. (16)

Волновое сопротивление в непроводящей среде:

. (17)

При падении плоской волны на плоскую границу раздела двух сред углы , указывающие направления распространения соответственно падающей, отраженной и преломленной волн связаны соотношениями:

, (18)

где – показатели преломления первой и второй сред.

Амплитуды отраженной (Е₁, Н₁) и преломленной (Е₂, Н₂) волн выражаются через амплитуды Е₀, Н₀ падающей волны по формулам Френеля:

а) если Е₀ нормальна к плоскости падения, то

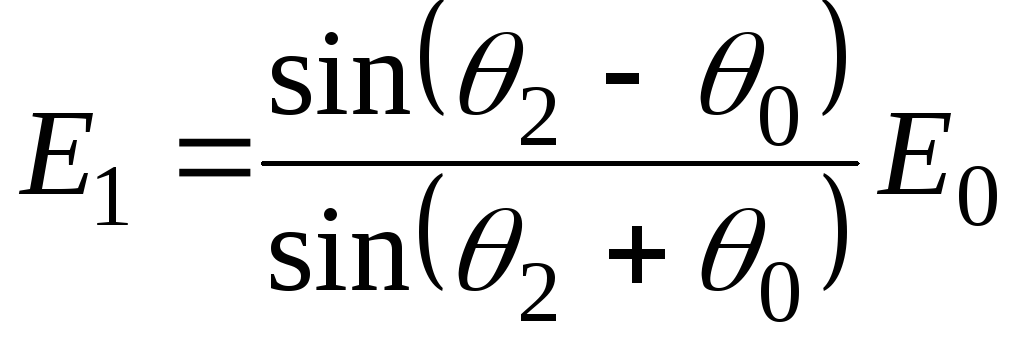, , (19)

б) если Н₀ нормальна к плоскости падения, то

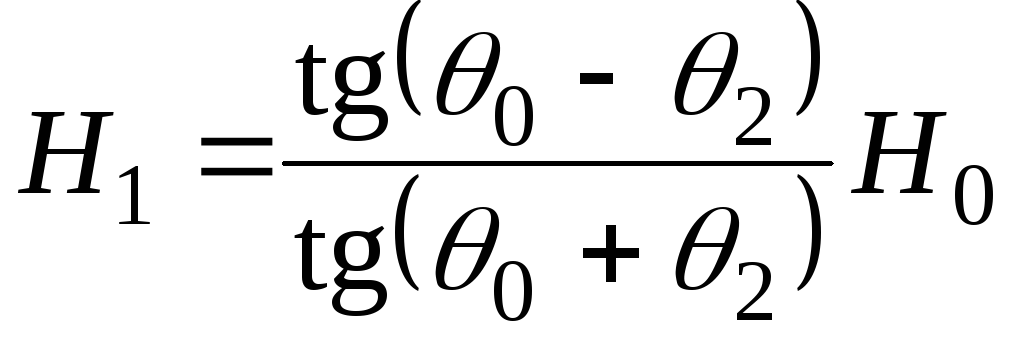, . (20)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. Перпендикулярно к поверхности проводника с электропроводностью и магнитной проницаемостью падает плоская электромагнитная волна частоты . Пренебрегая токами смещения по сравнению с токами проводимости, определить, на какой глубине внутри проводника электромагнитное поле волны ослабевает в е раз (е – основание натуральных логарифмов).

Решение

Выбрав систему координат так, как это показано на рисунке 1, можно записать для электромагнитного поля плоской волны в вакууме:

,

.

Электромагнитное поле в проводнике определяется уравнениями:

, (1)

. (2)

Нетрудно видеть, что

и, следовательно, уравнения (1) и (2) можно переписать в виде:

, (3)

. (4)

Продифференцировав уравнение (3) еще один раз по x и подставив из (4), получим уравнение для определения амплитуды магнитного поля волны:

. (5)

Тем же способом получается аналогичное уравнение для определения амплитуды электрического поля. Корни характеристического уравнения , соответствующего уравнению (5), равны:

.

Однако условию задачи удовлетворяет лишь второй корень k₂ (корню k₁ соответствует волна, амплитуда которой возрастает по мере продвижения в глубь проводника).

Таким образом, решения уравнений (3) и (4) мы должны записать в виде:

(6)

где и – амплитуды напряженностей электрического и магнитного поля волны при х = 0, т. е. на поверхности проводника.

Выражения (6) показывают, что электромагнитная волна ослабляется в е раз на глубине

.

2. Плоскополяризованная электромагнитная волна падает на границу раздела двух прозрачных () сред с показателями преломления и . Электрический вектор волны параллелен плоскости раздела сред. Найти коэффициент прохождения света во вторую среду.

Решение

Обозначив через и напряженности электрического поля соответственно в падающей, отраженной и преломленной волнах, запишем закон сохранения энергии и граничное условие .

Граничное условие , как показывает рисунок 2, можно записать в виде:

. (1)

Закон сохранения энергии требует, чтобы количество энергии, уносимой с единицы поверхности раздела сред отраженной волной, и энергии, проходящей во вторую среду из первой, было равно энергии, доставляемой указанной площадке падающей волной, т.е.

, (2)

где S – вектор Пойнтинга. Подставляя в (2)

,

находим:

,

откуда, используя закон преломления , окончательно получаем:

. (3)

Решая систему уравнений (1) и (3), находим:

, . (4)

Подставляя в (4) , и , находим далее:

, . (4)

С помощью выражений (4) и (5) находим следующие выражения для плотности потока энергии в отраженной и преломленной волне:

,

,

откуда искомые коэффициенты отражения и прохождения оказываются равными:

, . (6)

ЗАДАЧИ

1. Показать, что в плоской электромагнитной волне, распространяющейся в однородной среде, векторы и взаимно перпендикулярны между собой и каждый из них перпендикулярен к направлению распространения волны. Показать также, что у плоской электромагнитной волны .

2. Плоская электромагнитная волна, у которой

; ,

падает при х = 0 на нормальную к оси X плоскую поверхность проводника, простирающегося вправо до бесконечности. Пренебрегая отражением, определить производимое электромагнитной волной световое давление.

3. Плоский конденсатор состоит из двух параллельных слоев различных веществ. Первый слой толщиной d имеет диэлектрическую проницаемость и электропроводность, равную нулю; для другого слоя толщиной kd диэлектрическая проницаемость , а электропроводность имеет конечное значение. Показать, что в отношении распространения монохроматических плоских волн этот конденсатор ведет себя так, как если бы все пространство между его пластинами было заполнено однородной средой с диэлектрической проницаемостью

.

4. Определить затухание электромагнитных волн в среде при полном внутреннем отражении.

5. Определить амплитуды волн, отраженной от плоскопараллельной пластины и прошедшей через нее Толщина пластины d, диэлектрическая проницаемость . Найти условия, при которых отражение электромагнитных волн от пластины минимально.

6. Определить напряженности электрического и магнитного поля Е–ТМ волны, бегущей вдоль волновода прямоугольного сечения с идеально проводящими стенками. Найти также уравнения силовых линий электрического и магнитного поля в сечении XOY волновода.

7. Найти плотность поверхностного заряда и плотность поверхностного тока на стенках прямоугольного волновода, вдоль которого бежит волна Е–Т₁₁М частоты .