69
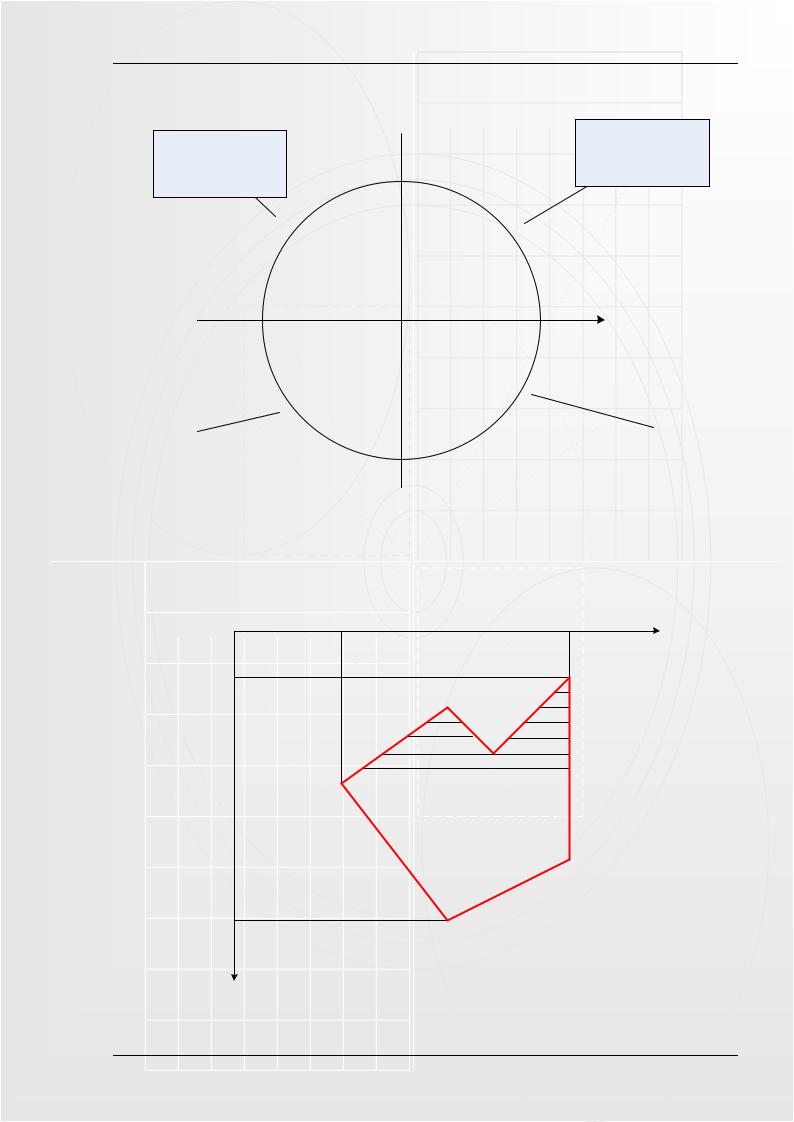
критерий ошибки Брезенхема используется для принятия решения об изменении величины x. Выбор постоянно изменяющейся (на +1 или -1) координаты зависит от квадранта (см. рис. 14.6).
Y 
Увеличение X на 1 Уменьшение X на 1 Увеличение Y на 1 Увеличение Y на 1
x = x −1 |
x = x +1 |
y = y +1 |
y = y +1 |
|
x = x −1 |
x = x +1 |
X |
|
|
||
|
y = y −1 |
y = y −1 |
|
Уменьшение X на 1 |
|
|
Увеличение X на 1 |
Уменьшение Y на 1 |
|
|
Уменьшение Y на 1 |
|
|
|
|
|
|
|
|
Рисунок 14.6. – Особенности обработки отрезков в разных квадрантах
Простейший алгоритм закрашивания замкнутой области
На лабораторной работе мы рассмотрим простейший алгоритм заливки замкнутой области, которая либо очерчена границей с кодом пикселя, отличающимся от кодов любых пикселей внутри области, либо закрашена пикселями с заданным кодом.
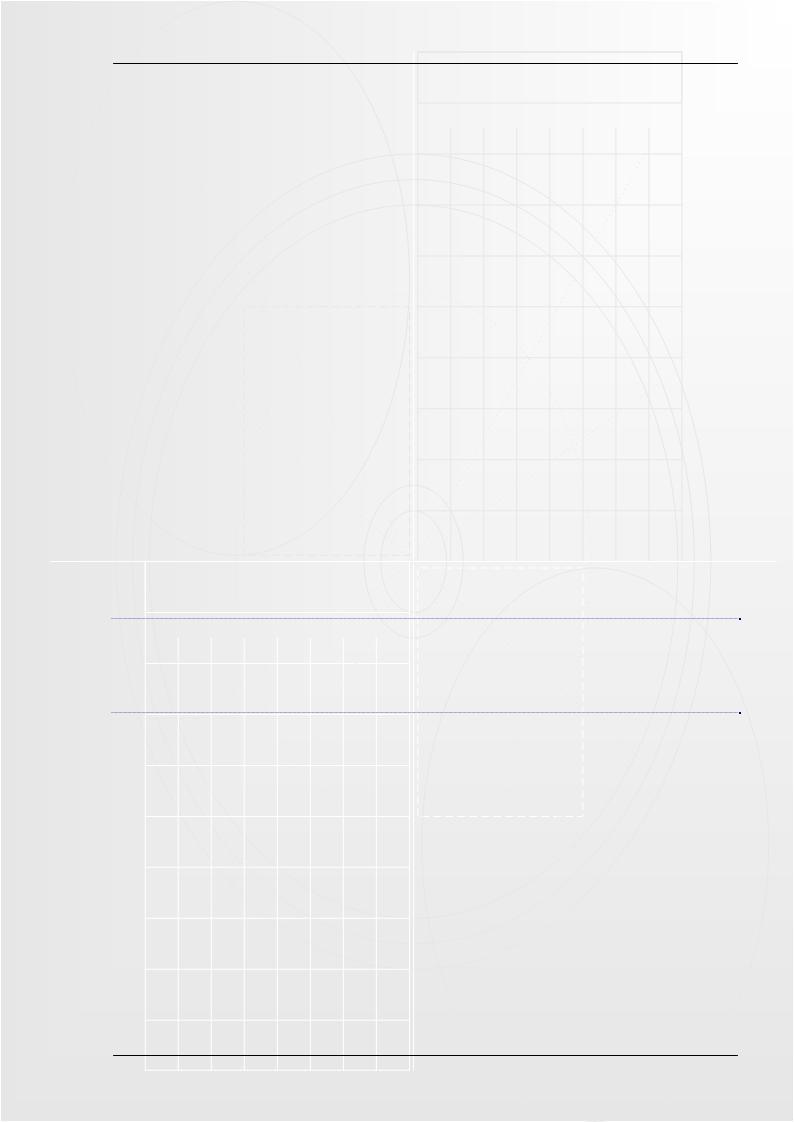
Рисунок 14.7. – Демонстрация алгоритма построчного заполнения |
70
В таком случае нам подойдёт алгоритм построчного заполнения. Идея основана на том, что соседние пиксели в строке скорее всего одинаковы и меняются только там где строка пересекается с ребром многоугольника.
Алгоритм представляет собой цикл вдоль оси Y, в ходе цикла выполняется поиск точек пересечения линии контура с соответствующими горизонталями (см. рис. 14.7):
1.Найти самую нижнюю и самую верхнюю вершины.
2.Выполнить цикл от Y=Y min до Y max:
a.Нахождение точек xi пересечения всех отрезков контура с горизонталью. Координаты этих точек занести в массив.
b.Сортировка массива точек по возрастанию x.
c.Вывод горизонтальных отрезков с координатами (x0 , y)−(x1 , y).
Задание
1.Разработайте функцию позволяющую чертить произвольный отрезок на основе прямого вычисления координат.
2.Разработайте функцию позволяющую чертить произвольный отрезок на основе инкрементного алгоритма Брезенхэма.
3.Разработайте функцию позволяющую закрашивать произвольную замкнутую область.
Для рисования замкнутой области можно воспользоваться методами Delphi. Прямоугольник выводит процедура:
procedure Rectangle(Left, Top ,Right ,Bottom: Integer);
Эллипс чертит процедура:
procedure Ellipse(Left, Top ,Right ,Bottom: Integer);
Произвольный многоугольник с любым числом вершин:
procedure Polygon(Points: array of TPoint);
Например, многоугольник с пятью вершинами можно нарисовать с помощью следующего кода:
var Arr : array [0..4] of TPoint; begin
Arr[0]:=Point(10,10); Arr[1]:=Point(20,10); Arr[2]:=Point(120,45); Arr[3]:=Point(120,200); Arr[4]:=Point(45,50); Form1.Canvas.Polygon(Arr);
end;