
- •Содержание
- •Рекомендации к проведению лабораторных работ
- •Комментарии в тексте программы
- •Компиляция и запуск программы на выполнение
- •Переменные и константы
- •Операторы и выражения
- •Оператор присваивания
- •Арифметические операции
- •Логические операции
- •Составной оператор begin..end
- •Условный оператор if..then
- •Оператор-селектор case..of
- •Операторы обработки циклов
- •Цикл с параметром for .. do
- •Цикл с предусловием while..do
- •Цикл с постусловием repeat..until
- •Процедуры break и continue
- •Оператор with..do
- •Процедуры и функции
- •Процедуры
- •Функции
- •1. Фундаментальные структуры данных
- •Общее понятие типа данных
- •Простой тип
- •Перечислимые типы данных
- •Поддиапазонны
- •Строковый тип
- •Структурные типы
- •Массивы
- •Записи
- •Множества
- •Представление структур в памяти
- •Задание
- •2. Работа с последовательностями, файлы
- •Доступ к файлу
- •Операции над файлами
- •Окончание файла
- •Пример работы с файлом
- •Задание
- •3. Анализ алгоритмов
- •Рост функций
- •Задание
- •4. Простейшие методы сортировки массивов
- •Оценка алгоритмов сортировки
- •Шейкер-сортировка
- •Сортировка простыми вставками
- •Сортировка бинарными вставками
- •Задание
- •5. Улучшенные методы сортировки массивов
- •Сортировка с помощью включений с уменьшающимися расстояниями (сортировка Шелла)
- •Пирамидальная сортировка
- •Сортировка с разделением (быстрая сортировка)
- •Задание
- •6. Сортировка последовательных файлов
- •Сортировка простым слиянием
- •Естественное слияние
- •Задание
- •7. Рекурсивные алгоритмы
- •Сравнение рекурсии и итерации
- •Задание
- •8. Динамические структуры данных, связные списки
- •Списки
- •Пример создания и заполнения списка
- •Задание
- •9. Нелинейные структуры данных
- •Граф
- •Бинарное дерево
- •Задание
- •10. Алгоритмы на графах
- •Алгоритмы обхода в глубину и по уровням
- •Построение минимального остовного дерева
- •Поиск кратчайшего пути
- •Задание
- •11. Поиск данных
- •Двоичный (бинарный) поиск элемента в массиве
- •Интерполяционный поиск элемента в массиве
- •Алгоритм Бойера-Мура
- •Задание
- •12. Хеширование
- •Отечественный стандарт хеширования
- •Создание хеш-функции
- •Хеш-функции для строковых значений, алгоритм Гонера
- •Задание
- •13. Методы сжатия текстовых данных
- •Метод “Running”
- •Словарные методы сжатия
- •Алгоритм Хаффмана
- •Задание
- •14. Алгоритмы вывода графических примитивов
- •Рисование отрезка
- •Прямое вычисление координат
- •Инкрементный алгоритм Брезенхэма
- •Простейший алгоритм закрашивания замкнутой области
- •Задание
- •15. Псевдослучайные последовательности
- •Метод середин квадратов
- •Линейный конгруэнтный метод
- •Генератор псевдослучайных чисел, поставляемый с системой
- •Оценка качества генератора ПСП
- •Задание
- •16. Параллельные алгоритмы
- •Пример многопоточного приложения
- •Задание
- •Задание на СКР
- •Вариант 1. Клеточные автоматы
- •Вариант 2. Раскрашивание карты
- •Вариант 3. Крисс-кросс
- •Вариант 4. Лабиринт
- •Список использованной литературы
- •Приложение A. Справочник по функциям Delphi
- •Операции с порядковыми типами
- •Математические функции и процедуры
- •Генерация псевдослучайного числа
- •Преобразование типов данных
- •Работа с памятью
- •Приложение Б. Компонент-сетка TStringGrid
- •Приложение В. Компонент-диаграмма TChart
- •Приложение Д. Элементарный поток – класс TThread

28
3. Анализ алгоритмов
Вид занятия – лабораторная работа Цель – исследование способов оценки качества алгоритмов
Продолжительность – 4 часа
Алгоритм (algorithm) – это любая корректно определённая вычислительная процедура, на вход которой подаётся некоторый набор значений, и результатом выполнения которой является выходной набор значений.
Хороший алгоритм обладает следующими качествами:
-Конечность. Алгоритм всегда должен заканчиваться после выполнения конечного числа шагов.
-Определённость. Каждый шаг алгоритма должен быть определён.
-Ввод. Каждый алгоритм имеет некоторое подмножество входных данных.
-Вывод. У алгоритма есть одно или несколько выходных данных.
-Эффективность. Алгоритм можно считать эффективным если все его операторы достаточно просты чтобы их можно было выполнить в течении конечного промежутка времени.
Прежде чем говорить об эффективности алгоритма необходимо убедиться, что он предоставляет правильное решение!
Один из первых шагов в понимании производительности алгоритмов – это эмпирический анализ. Например, если имеется два алгоритма способные решить одну и ту же задачу. Мы их запускаем и сравниваем время их выполнения.
Самым простым способом сравнения времени выполнения алгоритма может стать использование двух меток времени T1 и T2. Одна из них берётся в начале выполнения алгоритма, а вторая в конце. Разность T2 - T1 и есть время выполнения.
Метку времени можно получить с помощью функций:
function Time: TDateTime; function GetTime: TDateTime;
Обе функции идентичны, они возвращают системное время вашего компьютера. Кроме того, в нашем распоряжении имеется системная функция Windows:
function GetTickCount: DWORD;
которая возвращает количество миллисекунд прошедших с начала запуска компьютера. Её также можно применять для сравнения времени выполнения алгоритмов.
Математический анализ алгоритмов сводится к следующим действиям:
1.Выявление абстрактных операций из которых состоит алгоритм.
2.Определение частоты (количества раз) выполнения операций.
3.Моделирование данных поступающих на вход алгоритма
Рост функций
Большинство алгоритмов имеет главный параметр N, который значительно влияет на степень его выполнения. Например: степень полинома, размер файла при сортировке или поиске, количество символов в строке, и т.п. В большинстве случаев время выполнения алгоритма можно свести функциям представленным в таблице 3.1.
|
Таблица 3.1. – Оценочные функции |
|
|
|
Функция |
Описание |
Примечание |
|
1 |
Время выполнения программы постоянно. |
|
|
LogN |
Время выполнения программы является логарифмическим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
N |
Время выполнения программы является линейным |
|
|
|
|
||||
NLogN |
Время выполнения программы пропорциональное N Log N |
|
|
|
|
|||||
|
N 2 |
Время выполнения программы является квадратичным |
|
Алгоритмы с такими показате- |
||||||
|
N 3 |
Время выполнения программы является кубическим |
|
лями не могут считаться эф- |
||||||
|
2N |
Время выполнения программы экспоненциально |
|
|
фективными! |
|
|
|||
|
|
|
|
|
|
|||||
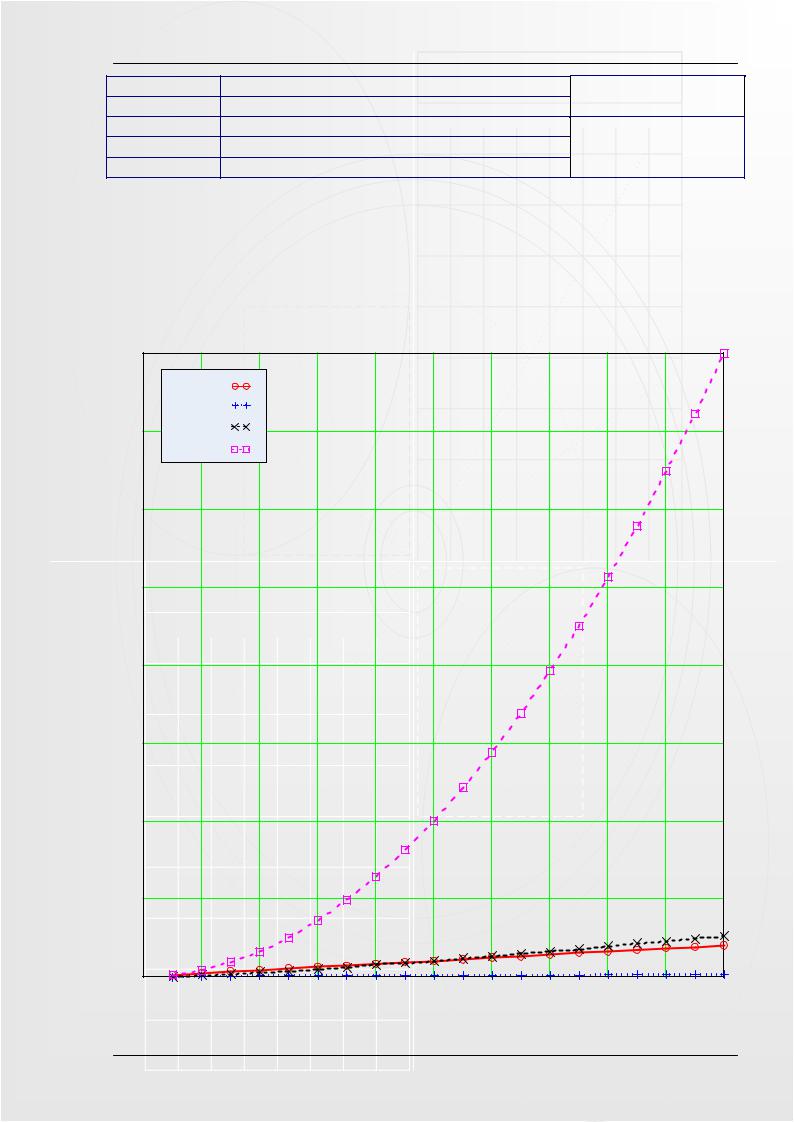
Для того, чтобы получить представление о величинах оценочных функций достаточно одного |
||||||||||
взгляда на представленный на рисунке 3.1 график. Заметьте, что в качестве параметра нами взята |
||||||||||
совсем небольшая величина N=20. Задумайтесь, что произойдет, если главный параметр функций |
||||||||||
составит более существенные значения. Например, в этом учебном пособии около 200 тысяч зна- |
||||||||||
ков. Чтобы было, если бы мы попытались найти все вхождения слова “алгоритм” в нашем мате- |
||||||||||
риале самым неэффективным способом – алгоритмом грубой силы, оцениваемым |
N 2 ? В этом |
|||||||||
случае нам потребуется около полутора миллионов операций сравнения! Если же мы воспользу- |
||||||||||
емся алгоритмом Бойера-Мура (главным героем 11 лабораторной работы), то мы сможем сокра- |
||||||||||
тить число сравнений на 25…40 процентов [13]! |
|
|
|
|
|
|
||||
400 |
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
Log(N) |
|
|
|
|
|
|
|
|
|
350 |
NLog(N) |
|
|
|
|
|
|
|
|
|
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2 |
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
250 |
|
|
|
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
NLog(N) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Log(N) |
N |
|
00 |
|
|
|
|
|
|
|
|
||
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
Рисунок 3.1. – Сравнительная оценка функций |
|
|
|
||||

30
Алгоритм, претендующий на высокое эффективного должен стремится к оценочной логарифмическим оценочным функциям.
Задание
1. Разработайте две процедуры поиска наибольшего общего делителя (НОД) произвольных чисел A и B. Первая процедура должна применять “лобовой” поиск (обычный перебор). Вторая процедура может использовать любой известный вам алгоритм поиска НОД, например алгоритм Евклида.
Подсказка:
Алгоритм Евклида. Дано два целых положительных числа а и b. Требуется найти наибольшее целое положительное число, которое разделит числа а и b без остатка.
1.Находим остаток. Разделим a на b и получим остаток от деления r для которого выполняется условие 0 ≤ r < b .
2.Сравнение с нулём. Если r=0, то b есть искомое число. Выполнение алгоритма прекращается.
3.Замещение. Если r ≠ 0 , то заменим пару чисел (a, b) парой (b, r) и перейдем к шагу
1.
При вычислении наибольшего общего делителя (a, b) с помощью алгоритма Евклида будет выполнено не более 5N операций деления с остатком, где N есть количество цифр в десятичной записи меньшего из чисел a и b.
2. Разработайте две процедуры получения факториала произвольного целого числа. Первая процедура основана на классическом решении, а вторая на формуле Джеймса Стирлинга:
n!≈ 2πn n n ,e
где: e – основание натурального алгоритма.
3. Разработайте две процедуры получения числа Фибоначчи. Первая процедура вычисляет запрошенное число с помощью классического рекуррентного соотношения:
F0 = 0, F1 =1, Fi = Fi−1 + Fi−2 ,i ≥ 2 .
Например: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … Вторая процедура получает число Фибоначчи с помощью значения золотого сечения φ и сопряжённого с ним значения φS :
φ= 1+2 5 ,φS = 1−2 5 .
Вэтом случае число Фибоначчи можно рассчитать с помощью выражения:
Fi = φi −φS ,
 5
5
после округления Fi до ближайшего целого числа.
4. Разработайте две процедуры проверки числа на простоту. Первая процедура должна основываться на обычном переборе, вторая – любой известный вам алгоритм, например тест простоты Рабина.
Подсказка:
Тест Рабина является вероятностным. Это означает, что он использует датчик случайных чисел и, таким образом, работает не детерминировано. Для входного целого числа m тест Рабина может выдать один из следующих двух ответов.
1.Число m является составным.
2.Не знаю.
Вслучае первого ответа число m действительно является составным, тест Рабина предъявляет доказательство этого факта. Второй ответ может быть выдан как для простого, так и

31
для составного числа m. Однако для любого составного числа m вероятность второго ответа не превышает 1/4. Ценность теста Рабина состоит именно в неравенстве, ограничивающем сверху вероятность второго ответа для произвольного составного числа m.
Таким образом, если мы применим 100 раз тест Рабина к числу m и получим 100 ответов "не знаю", то можно с большой вероятностью утверждать, что число m простое. Более точно, вероятность получения ста ответов "не знаю" для составного числа m не превышает
(1/ 4)100 , т.е. практически равна нулю. Тем не менее, тест Рабина не предъявляет доказательства того, что число m простое.
Тест Рабина
Мы проверяем простоту входного числа m. Допустим сразу, что число m нечетное. (Существует только одно четное простое число – 2.) Тогда число m – 1 четное. Представим его в виде
m −1 = 2t ×s
где s – нечетное число. Выберем случайное число b такое, что b ≠ 0 , b ≠1 (mod m), 1 < b < m
При выборе b используется датчик случайных чисел.
Используя алгоритм быстрого возведения в степень по модулю m, вычислим следующую последовательность элементов кольца Zm:
x0 =bs (mod m) ,
x1 = x0 ×x0 (mod m) ,
x2 = x1 ×x1 (mod m) ,
...
xt = xt−1 ×xt−1 (mod m)
(На каждом шаге мы возводим в квадрат число, полученное на предыдущем шаге.) Тест Рабина выдает ответ 'm - составное число' в случае, если
1)xt ≠1(mod m) или
2)в последовательности x0 , x1,..., xt имеется фрагмент вида ..., *, 1, ... где звездочкой обозначено число, отличное от единицы или минус единицы по модулю m.
Впротивном случае тест Рабина выдает ответ "не знаю". Последовательность x0 , x1,..., xt в этом "плохом" случае либо начинается с единицы, либо содержит (-1) где-нибудь не в конце.
После выполнения всех заданий проведите эмпирический и математический сравнительный анализ ваших алгоритмов.
