Разложение некоторых элементарных функций в ряд Тейлора.

Задача разложения функции в ряд Тейлора в окрестности точки решается в следующем порядке:

1. Находятся последовательно .

2. Записываются 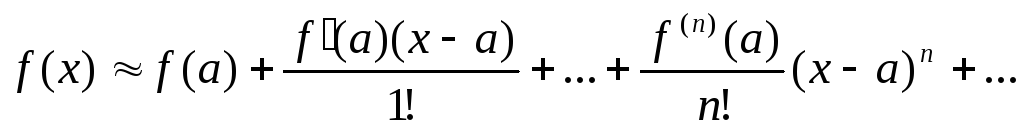(1).

3. Находим интервал сходимости ряда (1): .

4. Записываем остаточный член в каком-то виде.

5. Находим те точки , для которых.

После выполнения этих пунктов в (1) вместо можно поставить равенство.

Функция .

Пусть задана функция , она бесконечно дифференцируемая и , где.

Найдем коэффициенты разложения , тогда

-это ряд Маклорена для функции , который сходится к этой функции на всей числовой прямой.

Функция .

Найдем ее производные

Вычислим коэффициенты в формуле Тейлора:

. Пусть , тогда , если , то так как , то по теореме 2, можно утверждать, что ряд Тейлора сходится к функции.

.

Функция . Можно провести аналогично разложение, а можно разложить другим способом. Мы знаем, что степенной ряд можно дифференцировать в интервале его сходимости. Тогда .

Ряд Маклорена для функции.

Так как функция и ее производные не определены в точке, поэтому будем рассматривать функцию , которая определена , вместе с производными. Продифференцируем:

- как сумма бесконечно убывающей геометрической прогрессии (имеет сумму при).

Проинтегрируем этот ряд почленно по любому отрезку от до, где . Получим он сходится при. Проверим сходится ли ряд на границах интервала:

при ряд вообще суммы не имеет, приполучается знакочередующийся рядпо теореме Лейбница он сходится, покажем, что он сходится к, то есть. Воспользуемся теоремой (достаточным условием разложимости в ряд Тейлора). Для этого оценим остаточный член в формуле Лагранжа.при

Тогда .

Таким образом, , то есть ряд сходится при.

При ряд расходится, так как не выполнено необходимое условие сходимости ряда, так как.

Разложение степенной функции в ряд Тейлора.

Рассмотрим функцию . (5).

Область сходимости ряда . на границе интервала надо проверять отдельно для каждого конкретного ряда

Отметим наиболее часто встречающиеся частные случаи биномиального ряда:

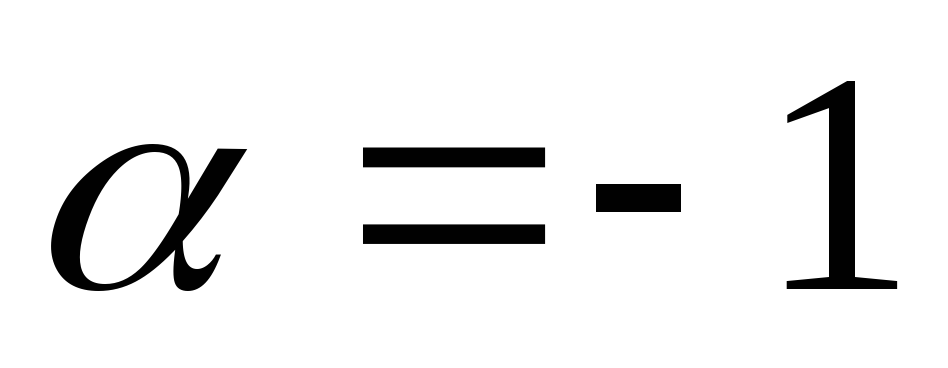1. , тогда - бесконечно убывающая геометрическая прогрессия, сходится при .

2. , тогда

3. , тогда

Используя свойство степенных рядов о почленном интегрировании и дифференцировании внутри области сходимости можно получить следующие разложения:

Пример 1: сходится при . Проинтегрируем внутри отрезка сходимости:Пример 2:

Сходится при . Проинтегрировав понаполучим: .

Дробно-рациональная функция.

- многочлены. Чтобы разложить в ряд Тейлора, вначале приводим к правильной дроби, далее полученную дробь разбиваем на сумму более простых методом неопределенных коэффициентов. Эти более простые дроби раскладываем в ряд Тейлора, используя разложение в геометрическую прогрессию.

.

.

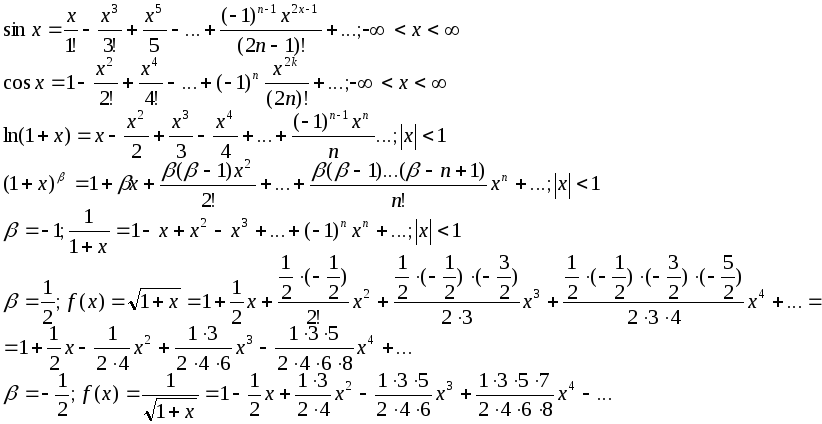
Ряд Тейлора. Разложение основных элементарных функций в степенные ряды.

Теорема: Всякая функция, бесконечно дифференцируемая в интервале , то есть, может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора.

, если в этом интервале выполняется условие , где- остаточный член формулы Тейлора,. Приполучается ряд Маклорена:. Если в некотором интервале, содержащем точку, при любом выполняется неравенство , где- положительная постоянная, тои функцияразложима в ряд Тейлора.