16.4 Разложение функции в степенной ряд. Единственность разложения. Ряд Тейлора.

Для того, чтобы функция разлагалась в степенной ряд необходимо, чтобы она была бесконечно дифференцируемой, но это условие не является достаточным.

Определение: Говорят, что функция разлагается на данном промежутке, если существует степенной ряд, где, который сходится на этом промежутке к данной функции так, что(1).

В качестве промежутка обычно рассматривается окрестность.

Задача разложения функции в степенной ряд заключается прежде всего в том, чтобы получить возможность приближенного вычисления значений функции через частичную сумму ряда (1).Далее это может использоваться для приближенного вычисления интегралов, корней уравнения. Причем степень приближения может оцениваться с любой точностью.

Теорема: Если в некотором интервале, содержащем точку функцияразлагается в ряд по степеням, то такое разложение единственно.

Доказательство: Рассмотрим интервал и пусть в этом интервале имеет место разложение (1), в котором -неизвестные пока коэффициенты. Найдем эти коэффициенты: продифференцируемраз:

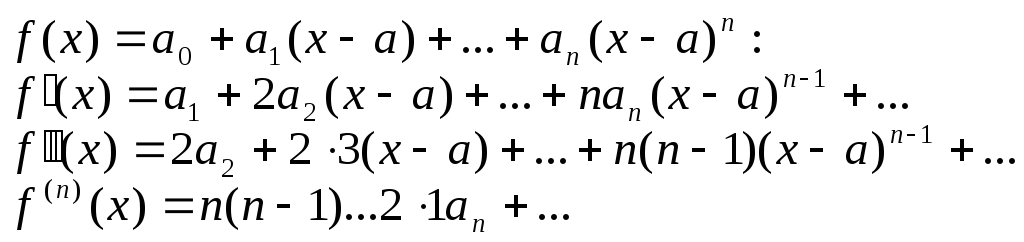
Полагая в этих равенствах , выразим коэффициенты разложения через значения функций в точке, т.е.(2).

Отсюда следует единственность разложения функции в ряд (1), т.к. коэффициенты разложения определяются однозначно через функцию и ее значения в точке.

Определение: Степной ряд с коэффициентами, вычисленными по формулам (2), т.е. ряд вида называется рядом Тейлора для функциив окрестности точки. Если, то получим

(4)- называемый рядом Маклорена.

Замечание: Бесконечная дифференцируемость функций не является достаточным условием разложимости функций в ряд Тейлора.

Теорема 1: Для того, чтобы бесконечно дифференцируемая функция могла быть разложена в ряд Тейлора на некотором интервале, необходимо и достаточно, чтобы остаточный член в формуле Маклорена стремился к нулю на этом интервале, то есть.

Доказательство: (Достаточное) Если функция имеет производную всех порядков в окрестности точки , то в формуле Тейлора числоможно брать сколь угодно большим.

Допустим, что в рассматриваемой окрестности остаточный член при:, тогда переходя в (3) к пределу при, получим бесконечный ряд - ряд Тейлора.(3).

Последнее равенство справедливо лишь при условии . В этом случае написанный ряд сходится и его сумма равна. Действительно, , где . Тогда , т.к.. Но есть-я частичная сумма ряда (3), ее предел равен сумме ряда, стоящего в правой части равенства (3). Следовательно, равенство (3) справедливо.

(Необходимое):Пусть представляется формулой Тейлора (3), тогда , но так как ряд сходится, то можно записать .

Теорема 2: Пусть бесконечно дифференцируемая функция в некоторой точкеи некоторой ее окрестности, тогда ряд Тейлора сходится к этой функции, если последовательность е производныхравномерно ограничена.

Доказательство: Пусть последовательность производных -равномерно ограничена, то есть, тогда(остаточный член в формуле Лагранжа). Используя условие теоремы можно оценить остаточный член в формуле Лагранжа:(так как последовательность равномерно ограничена). Рассмотрим вспомогательный ряд-он по признаку Даламбера сходится, тогда(необходимое условие сходимости), но тогда. А отсюда по теореме 1 следует, что ряд Тейлора сходится к данной функции.

Замечание: Если для какой-нибудь функции формально написан ряд Тейлора, то чтобы доказать, что написанный ряд представляет данную функцию, нужно либо доказать, что остаточный член стремится к нулю, либо каким-нибудь иным способом убедиться, что написанный ряд сходится к данной функции.