Можно показать, что функции и- линейно независимы. Поэтому общее решение уравнения (3) имеет вид

y=C₁e^kx+C₂xe^kx

Пример.

y^//+6y^/+9y=0

k²+6k+9=0

(k+3)²=0

k₁=k₂=-3

y=C₁e^-3x+C₂xe^-3x

3 случай. Корни и- комплексные.

Можно показать, что общее решение уравнения (3) в этом случае есть

.

Пример.

Корни характерного уравнения	Общее решение дифференциального уравнения.
k1k2R k1=k2=k R k1=+i, k2=-i	y=C1ekx+C2xekx y=ex(C1cosx+C2sinx)

21.3.

Рассмотрим решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами:

1. y^//+py^/+qy=f(x), где p,qR, f(x) – непрерывная функция в интервале (a,b).

Справедлива теорема.

Теорема. Общее решение неоднородного уравнения (1) равно сумме общего решения соответствующего однородного уравнения (y^//+py^/+qy=0) и любого частного решения данного неоднородного уравнения:

–общее решение соответствующего однородного уравнения, z – частное решение неоднородного уравнения.

Вид частного решения неоднородного уравнения зависит от вида правой части этого уравнения. Рассмотрим некоторые частные случаи.

f(x)	Особенности характерного уравнения k2+pk+q=0	Вид частного решения
Pn(x)	q0	z=Pn(x), Pn(x) – с неопределенным коэффициентом
	q=0,p0	z=xPn(x)
	p=0, q=0	z=x2Pn(x)
aebx	bk1, bk2	z=Aebx
	b=k1, bk2	z=Axebx
	b=k1=k2	z=Ax2ebx
acosx+bsinx	p0, q2	z=Acosx+Bsinx
	p=0, q=2	z=x(Acosx+Bsinx)

Примеры. Найти общие решения дифференциального уравнений.

1. y^//-9y=2-x

y^//-9y=0

k²-9=0

k₁=3 k₂=-3

y^- =C₁e^3x+C₂e^-3x

q=-90

z=A₁x+A₀

z^/=A₁

z^//=0

0-9(A₁x+A₀)=2-x

-9A₁x-9A₀=-x+2

2. y^//-y^/=4+x

k²-k=0

k₁=0, k₂=1

y^-=C₁+C₂x

q=0

z=x(A₁x+A₀)=A₁x²+A₀x

z^/=2A₁x+A₀

z^//=2A₁

2A₁-2A₁x-A₀=4+x

3. y^//=x-3

k²=0

k₁=k₂=0

y^-=C₁+C₂x

z=(A₁x+A₀)x²=A₁x³+A₀x²

z^/=3A₁x²+2A₀x

z^//=6A₁x+2A₀

6A₁x+2A₀=x-3

4. y^//-2y^/-3y=x²

k²-2k-3=0

k₁=3 k₂=-1

y^-=C₁e^3x+C₂e^-x

z=A₂x²+A₁x+A₀

z^/=2A₂x+A₁

z^//=2A₂

2A₂-4A₂x-2A₁-3A₂x²-3A₁x-3A₀=x²

5. y^//+y^/=e^-x

k²+k=0

k₁=0 k₂=0

y^-=C₁+C₂e^-x, b=-1=k₂

z=Axe^-x

z^/=Ae^-x-Axe^-x

z^//=-Ae^-x-Ae^-x+Axe^-x=-2Ae^-x+Axe^-x

-2Ae^-x+Axe^-x+Ae^-x-Axe^-x=e^-x

-Ae^-x=e^-x

-A=1

A=-1

Z=-xe^-x

y=C₁+C₂e^-x-xe^-x

6. y^//-by^/+9y=e^3x

k²-6k+9=0

k₁=k₂=3=b

y^-=C₁e^3x+C₂xe^3x

z=Ax²e^3x

z^/ = 9Axe^3x+3Ax²e^3x=e^3x(2Ax+3Ax²)

z^//=3(2Ax+3Ax²)e^3x+(2A+6Ax)e^3x=e^3x(12Ax+9Ax²+2A)

(9Ax²+12Ax+2A)e^3x-6e^3x(2Ax+3Ax²)+9Ax²e^3x=e^3x

9Ax²+12Ax+2A-12Ax-18Ax²+9Ax²=1

2A=1

7. y^//+6y=e^2x

k²+6=0

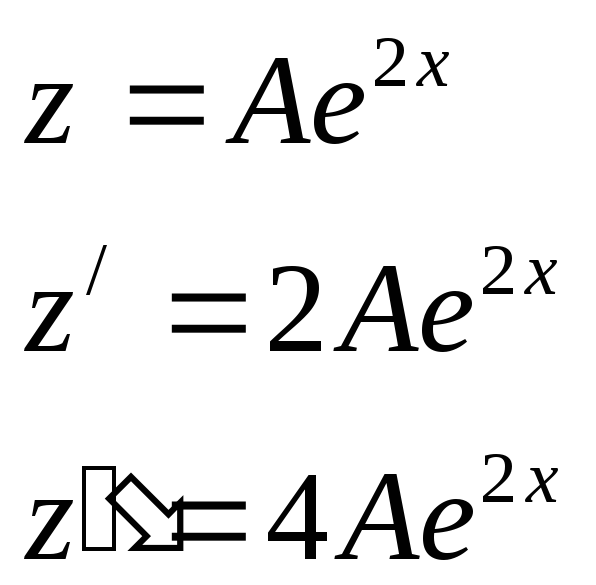
4Ae^2x+6Ae^2x=e^2x

10Ae^2x=e^2x

10A=1

A=,

8. y^//+100y=sin2x

k²+100=0

k₁=-10i, k₂=10i

y^-=C₁cos10x+C₂sin10x

p=0, q=100, =2, q²

z=Acos2x+Bsin2x

z^/=-2Asin2x +2Bcos2x

z^//=-4Acos2x-4Bsin2x

-4Acos2x-4Bsin2x+100Acos2x+100Bsin2x=sin2x

96Acos2x+96Bsin2x=sin2x

9. y^//+4y=2cos2x+sin2x

k²+4=0

k₁=2i k₂=-2i

y^-=C₁cos2x+C₂sin2x

p=0, q=4, =2, q=

z=x(A cos2x+Bsin2x)

z^/=Acos2x+Bsin2x+x(-2Asin2x+2Bcos2x)

z^//=-2Asin2x+2Bcos2x+(-2Asin2x+2Bcos2x)+x(-4Acos2x-4Bsin2x)=

=-4Asin2x+4Bcos2x+x(-4Acos2x-4Bsin2x)=-4Asin2x+4Bcos2x+x(-4Acos2x-4Bsin2x)+4x(Acos2x+Bsin2x)=2cos2x+sin2x

-4Asin2x+4Bcos2x=2cosx+sin2x

21.4

Линейным дифференциальным уравнением n-го порядка называется уравнение вида

y⁽ⁿ⁾+p_n-1(x)y^(n-1)+…+p₁(x)y^/+p₀(x)y=f(x) (1)

(a<x<b)

где f(x), p₀(x),…p_n-1(x) – заданные непрерывные на интервале (a,b) функции.

Обозначим левую часть (1) Ln[y]=L[y] ее называют линейным дифференциальным оператором n – го порядка.

Оператор L[y] обладает следующими свойствами:

1. L[Сy]=СL[y] – однородность оператора;

2. L[y₁+у₂]=L[y₁]+L[y₂] – аддитивность оператора.

Однородный и аддитивный оператор называется линейным.

Пример.

Пусть L[y]=у^//+у, тогда L[sinx]=-sinx+sinx=0

L[x²]=2+x²