
- •Дифференциальные уравнения Лекция 19. Дифференциальные уравнения первого порядка
- •Пусть дано дифференциальное уравнение первого порядка
- •Это уравнение называется уравнением с разделяющимися переменными. Разделим почленно на :
- •Можно показать, что функции и- линейно независимы. Поэтому общее решение уравнения (3) имеет вид
- •При введенных обозначениях уравнение (1) можно записать
- •Лекция 22. Дифференциальные уравнения с частными производными. Основные понятия. Линейные уравнения n-го порядка с частными производными первого порядка.
Дифференциальные уравнения Лекция 19. Дифференциальные уравнения первого порядка
План лекции
19.1. Задачи, приводящие к дифференциации уравнениям.
19.2. Основные понятия о дифференциальных уравнениях.
19.3. Уравнение первого порядка с разделяющимися переменными.
19.4. Однородные уравнения.
19.5. Дифференциальные уравнения, приводящиеся к однородным.
19.6. Линейные уравнения и уравнения Бернулли.
19.7. Дифференциальные уравнения в полных дифференциалах.
19.1
В различных областях науки и техники весьма часто выражаются задачи, для решения которых требуется решить одно или несколько уравнений, содержащих производные искомых функций. Такие уравнения называются дифференциальными. Рассмотрим несколько задач, приводящих к дифференциальным уравнениям.
Задание 1.на плоскости ХОУ найти кривую, проходящую через О(0;0), у которой угловой коэффициент касательной, проведен к любой точке кривой, равен удвоенной абсциссе точки касания.
Пусть у = f(x) – уравнение искомой кривой. По условию известно, что в каждой точке M(x;f(x)) есть касательная к этой кривой, угловой коэффициент которой, то есть f/(x) равняется 2х. Найти уравнение кривой.
Таким
образом, имеем
![]() (1).
(1).
Из
(1) следует, что y
= f(x)
есть первообразная для 2х.
Следовательно,
![]() (2).
(2).

Из
(2) следует, что дифференциальное уравнение
(1) имеет бесконечное множество решений,
то есть уравнению (1) удовлетворяет не
одна кривая, а бесконечное множество
парабол. Чтобы из этого множества кривых
выбрать нужную кривую, надо воспользоваться
тем, что искомая кривая проходит через
точку О(0;0). Следовательно, координаты
О должны удовлетворять (2). Поэтому О
= О + С, то
есть С = О.
Значит, искомая кривая будет
![]() .
.
Задание
2. Найти закон
уравнения свободного падающего в пустоте
тела, если пройденный путь начинает
отсчитываться от момента времени t
= 0 и начальная
скорость падения равна нулю. Скорость
в этом случае выражается, как известно,
формулой
![]() .
.
Решение.
![]() (3)
следовательно, S
– первообразная для gt,
следовательно
(3)
следовательно, S
– первообразная для gt,
следовательно
![]() .
Имеем
.
Имеем![]() .
.![]() следовательно
следовательно![]() ,
то
,
то![]() ,
то есть
,
то есть![]() .
.
Задание 3. Пусть тело имеющее температуру Q0 в момент времени t=0, помещено в среду температуры Q(Q0>Q). Требуется найти закон, по которому изменяется температура тела в зависимости от времени. Искомая температура есть функция от времени, которую обозначают через Q(t).
Из
функции известно, что скорость движения
тела пропорциональна разности температур
тела и окружающей среды. Учитывая, что
функция Q(t)
убывает, в силу максимального смысла
произведения получаем
![]() ,
гдеk
– коэффициент пропорциональности.
,
гдеk
– коэффициент пропорциональности.
![]() ,
,![]() .
.
Заметим, что уравнение (4) при Q=0 так же записывает радиоактивный распад.
В
рассмотренных задачах мы приходим к
дифференциации уравнения вида
![]() .
Это уравнение является простейшим
дифференциальным уравнением. Однако в
большинстве случаев естественные и
технические процессы описываются
гораздо более общими и сложными
дифференциальными уравнениями.
.
Это уравнение является простейшим
дифференциальным уравнением. Однако в
большинстве случаев естественные и
технические процессы описываются
гораздо более общими и сложными
дифференциальными уравнениями.
19.2.
Дифференциальным уравнением называется соотношение, связывающее независимую переменную х, искомую функцию y = f(x) и ее производные. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком данного уравнения.
Общий вид дифференциального уравнения: F(x,y.y/,…y(n)) = 0 (1).
Причем F(x,y.y/,…y(n)) может не зависеть от некоторых величин x,y.y/,… Но если это уравнение n-го порядка, то от y(n) обязательно зависит.
Например,
у/
+ ху = 0, у//+2у/
= 1,
![]()
1-го порядка 2-го порядка 1-го порядка.
Всякая
функция
![]() ,
которая, будучи подставлена в уравнение
(1), обращает его в тождество, называетсярешением
этого уравнения.
,
которая, будучи подставлена в уравнение
(1), обращает его в тождество, называетсярешением
этого уравнения.
График решения обыкновенного дифференциального уравнения n-го порядка будем называть интегральной кривой этого уравнения.
Например,
является ли функция y
= 1+2e-4x
решением дифференциального уравнения
а)
![]() ,
б)
,
б)![]() .
Найдему/
и у//
и подставим у,
у/,
у//
в данные
уравнения:
.
Найдему/
и у//
и подставим у,
у/,
у//
в данные
уравнения:
![]() ,
,
![]()
а)
![]() б)
б)![]()
0
= 0 – верно
![]() - ложно.
- ложно.
Следовательно, данная функция решения дифференциального уравнения а) не является решением дифференциального уравнения б).
Дифференциальное уравнение первого порядка называется соотношение вида F(x,y,y/) = 0 (2) - в полном виде.
Относительно
y/:
![]() - в явном или естественном его можно
разрешить. (2/).
- в явном или естественном его можно
разрешить. (2/).
Решением
дифференциального
уравнения первого порядка называется
функция
![]() ,
зависящая от переменойx
и от произвольной постоянной C,
обращающая уравнение (2) в верное
равенство.
,
зависящая от переменойx
и от произвольной постоянной C,
обращающая уравнение (2) в верное
равенство.
Иногда решение уравнения может быть получено и неявной форме: Ф(х,у,с) = 0 или Ф(х,у) = С.
Решить данное дифференциальное уравнение – значит найти его общее решение в той или иной форме.
Решение, которое получается из общего решения при котором фиксированном значение произвольной постоянной C, называется частным решением.
Частное решение выделяется из общего с помощью так называемого начального условия.
Условие, что при х = х0 функция у должна равняться заданному числу у0 называется начальным условием.
Пример.
По общему решению дифференциального
уравнения у
= сх2
+ х2sinx.
Найти частное решение удовлетворяющее
начальному условию
![]()
Тогда
частное решение имеет вид:
![]() .
.
Общим
решением
дифференциального уравнения n-го
порядка F(x,y,…y/)
= 0(1)
называется функция
![]() ,
зависящая отn
произвольных постоянных и образующая
уравнение (1) в тождество.
,
зависящая отn
произвольных постоянных и образующая
уравнение (1) в тождество.
Решение, получаемое из общего при закреплении постоянных С1, С2,,….Сn называются частными.
Пусть
при заданном значении х
= х0
функция у
и ее первые (n-1)
производная принимают значения:
![]() .
Эти условия называются начальными. С
их помощью можно выделить из общего
решения единственное частное решения.
.
Эти условия называются начальными. С
их помощью можно выделить из общего
решения единственное частное решения.
Пример.
По общему решению дифференциального
уравнения
![]() .
Найти частное отвечающее условию
.
Найти частное отвечающее условию![]() (так как в общем решении 2 постоянных,
то это решение дифференциального
уравнения 2-го порядка).
(так как в общем решении 2 постоянных,
то это решение дифференциального
уравнения 2-го порядка).
![]() ,
,
![]() ,
,
 ,
,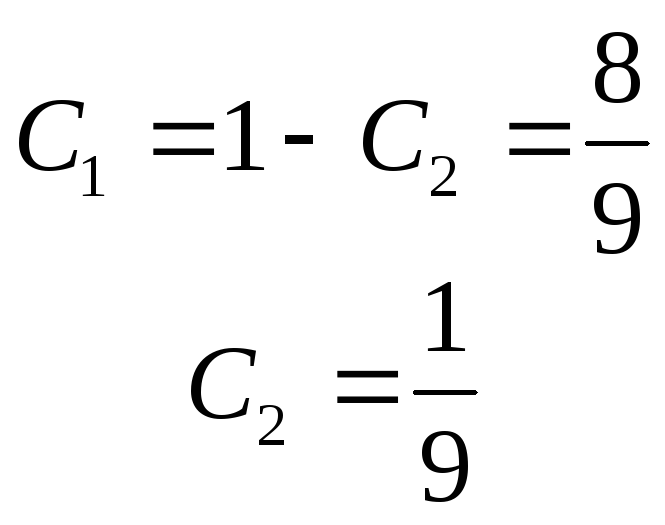 ,
,
![]() -
частное решение.
-
частное решение.
Остановимся далее на отдельных видах дифференциальных уравнений и методах их решения.
19.3.
