Вопросы, выносимые на обсуждение
1. Причины расширения множества действительных чисел до множества комплексных.
2. Алгебраическая форма записи комплексного числа и её геометрическая интерпретация.
3. Тригонометрическая форма записи комплексного числа и её геометрическая интерпретация.
4. Показательная форма комплексного числа.
Методические рекомендации
Для подготовки к занятию дома
Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.
Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.
Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.
Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.
Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.
На занятии по указанию преподавателя
Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.
В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.
Дома
1. Закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.
2. Подготовьтесь к самостоятельной работе №17 по теме «Комплексные числа», примерный вариант работы Вы можете найти в программе дисциплины.
Рекомендуемая литература
[1] глава 7 пп 7.7.
[2] часть 2, глава III § 7.
Примеры решения типовых задач
1.
Решите уравнение
во множестве
комплексных чисел.
Решение. Квадратное уравнение во множестве комплексных чисел всегда имеет два корня. Вычислим дискриминант:
,
следовательно, данное уравнение имеет
два комплексных сопряженных корня.
Найдем их:
или
,
отсюда
.
2. Изобразите
комплексные числа
Р
ешение.Числа заданы в алгебраической форме.
Согласно геометрической интерпретации
число
изображается точкой
.
Следовательно,
изображается точкой (0; -3), число
изображается
точкой (-1; 1). Заметим,
что число
является чисто мнимым, поэтому оно
расположено на оси
.
Комплексные числа
можно также интерпретировать как радиус
вектора полученных точек, т.е.
и
.
3. Запишите
числа
и
в тригонометрической и показательной
формах.
Решение.
Тригонометрическая форма записи
комплексного числа имеет вид
,
где
– модуль (длина радиус- вектора,
изображающего комплексное число,
),
– аргумент комплексного числа (угол
между положительным направлением оси
и радиус-вектором, изображающем это
число,
).
Учитывая приведенную
в задаче 1 геометрическую интерпретацию,
получаем
.
Для нахождения
модуля числа
воспользуемся формулой
,
а аргумент
находим из условий
.
Тогда
,
,
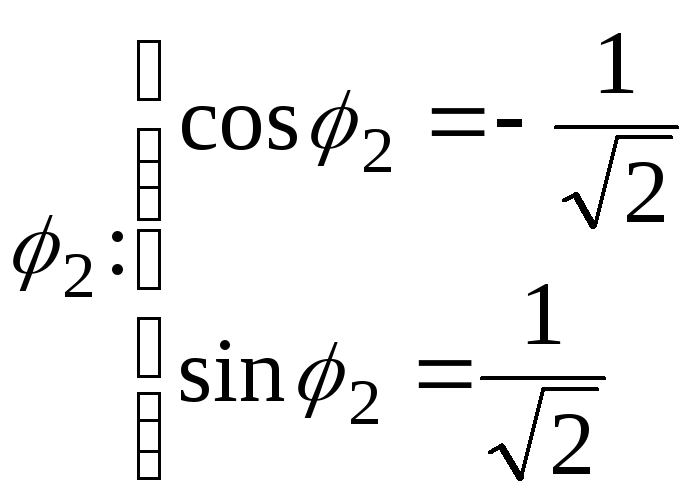следовательно
,
т.е.
.
Получаем
- тригонометрическая форма числа
.
Показательная
форма комплексного числа имеет вид
,
где
– модуль,
– аргумент. Поэтому
– показательные формы заданных
комплексных чисел.
4. Запишите
число
в алгебраической форме.
Решение. Сводя аргумент тригонометрических функций к острому углу и подставляя значения косинуса и синуса, имеем
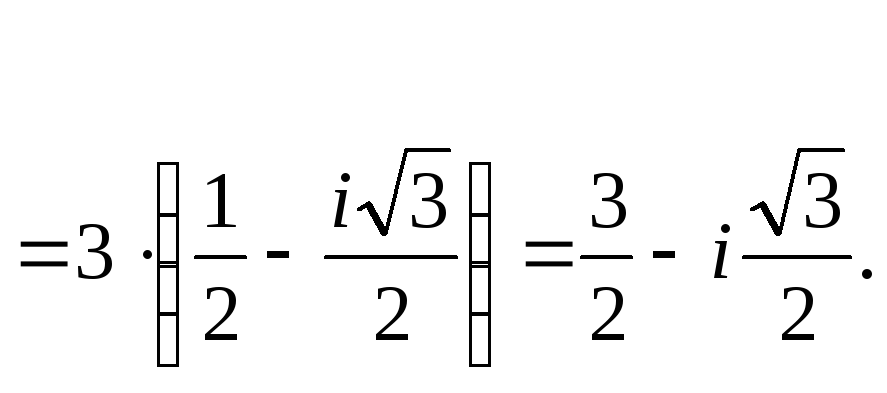
5. Вычислите в алгебраической форме:
а)
;
б)
;
в)
;
г)
,
если
;
.
Решение.
а)
Пользуясь правилом сложения комплексных
чисел в алгебраической форме, имеем
.
б)
Пользуясь правилом вычитания комплексных
чисел в алгебраической форме, имеем
.
в)
Комплексные числа в алгебраической
форме умножаются как двучлены, при этом
учитываем, что
,
поэтому имеем
.
г)
Чтобы разделить два комплексных числа
в алгебраической форме, числитель и
знаменатель умножаем на число сопряженное
знаменателю, отсюда имеем
.
6. Вычислите в тригонометрической форме:
а)
;
б)
;
в)
;
г)
,
если
,
.
Решение.
а) По правилу умножения комплексных чисел в тригонометрической форме, имеем
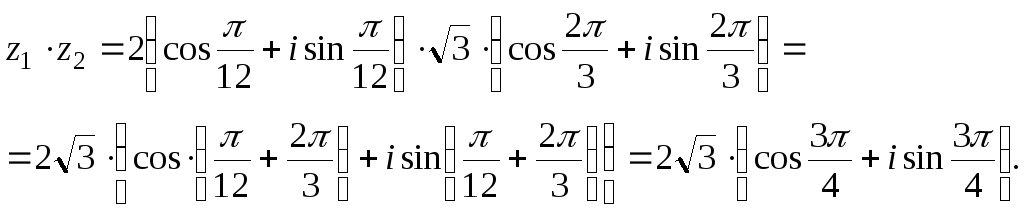
б) По правилу деления комплексных чисел в тригонометрической форме, имеем
.
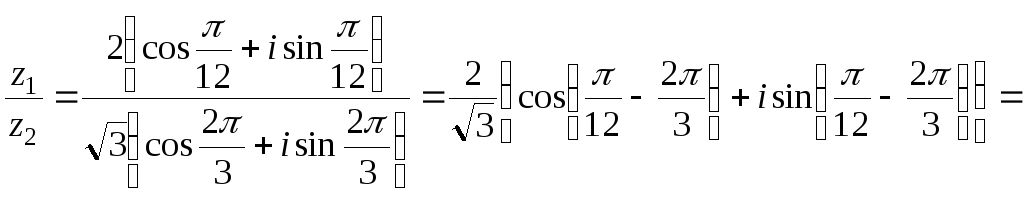
в) Возведение в натуральную степень комплексных чисел в тригонометрической форме проводим по формуле Муавра:
поэтому
г) Корень n-ой степени во множестве комплексных чисел имеет n значений, которые находим по формуле:
,
k=0,1,..,
n-1.
Таким образом,
,
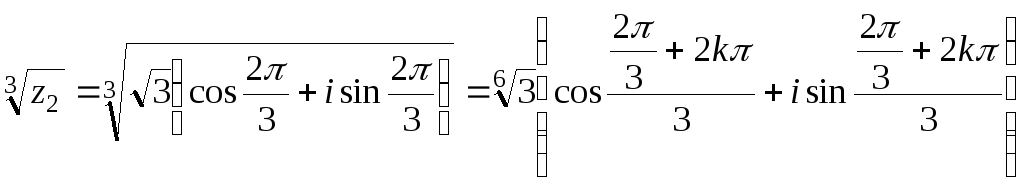k=0,1,2.
При k=0, 1, 2 получим три различные значения корня 3-ей степени:
при k=0
;
при k=1
;
при
k=2
.