
- •Практическое занятие № 25
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Примеры решения типовых задач
- •Теоретические задания
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Практические задания
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Задания для самостоятельной работы дома
- •Практическое занятие № 28
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Практические задания
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Практические задания
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Практические задания
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Примеры решения типовых задач
- •Теоретические задания для развития и контроля владения компетенциями
- •Практические задания
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Примеры решения типовых задач
- •Теоретические задания для развития и контроля владения компетенциями
- •Практические задания
- •Практическое занятие № 33
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Примеры решения типовых задач
- •Теоретические задания для развития и контроля владения компетенциями
- •Практические задания для развития и контроля владения компетенциями Задания, решаемые в аудитории
- •Задания для самостоятельной работы дома
- •Практическое занятие № 34
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Примеры решения типовых задач
- •Теоретические задания для развития и контроля владения компетенциями
- •Практические задания для развития и контроля владения компетенциями Задания, решаемые в аудитории
- •Задания для самостоятельной работы дома
- •Практическое занятие № 35-36
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Примеры решения типовых задач
- •Теоретические задания для развития и контроля владения компетенциями
- •Практические задания для развития и контроля владения компетенциями Задания, решаемые в аудитории
- •Задания для самостоятельной работы дома
- •Практическое занятие № 37
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Практические задания для развития и контроля владения компетенциями
- •1) 2)3)4)
- •Практическое занятие № 38
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями Вопросы для подготовки к контрольной работе
- •Практические задания
- •Для развития и контроля владения компетенциями
- •Примерный вариант контрольной работы № 3
- •Тема «Интегральное исчисление функции одной переменной»
Практические задания
для развития и контроля владения компетенциями
Задания, решаемые в аудитории
Вычислите интегралы:
а)
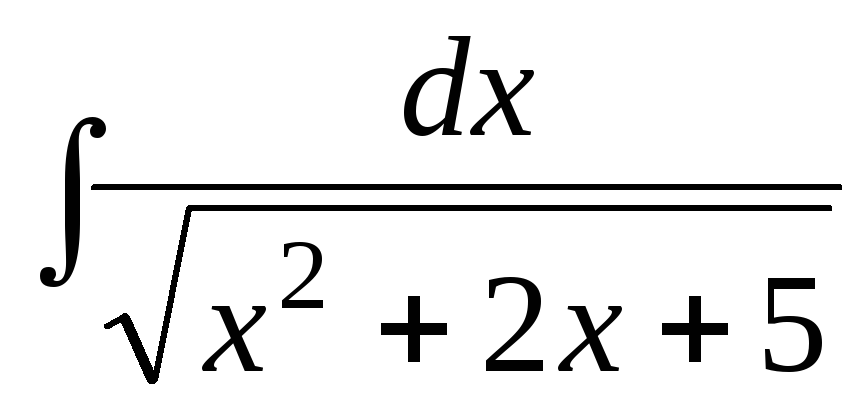 ;
б)
;
б)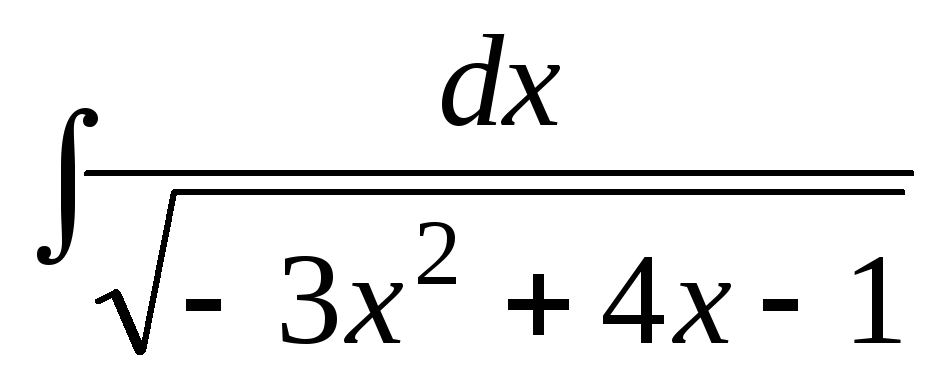 ;
в)
;
в)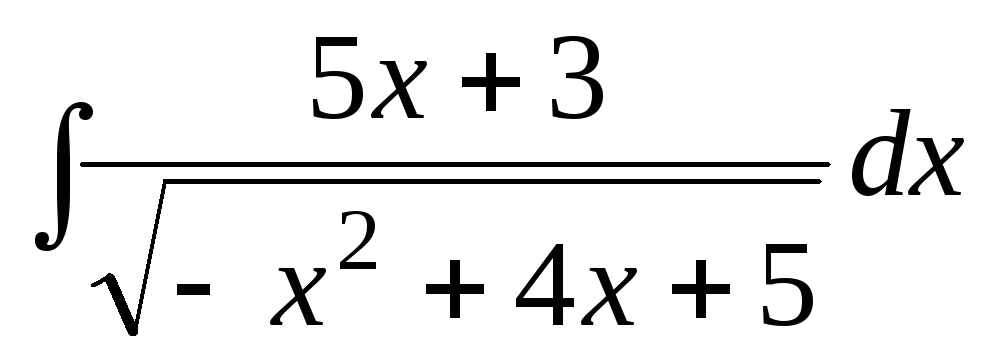 .
.а)
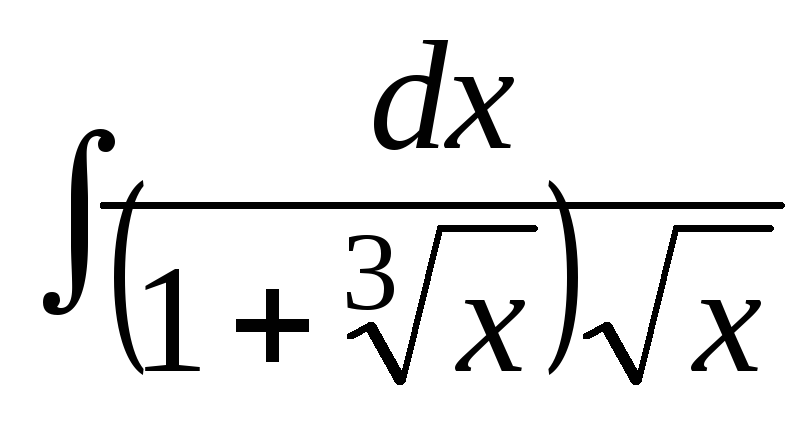 ;
б)
;
б)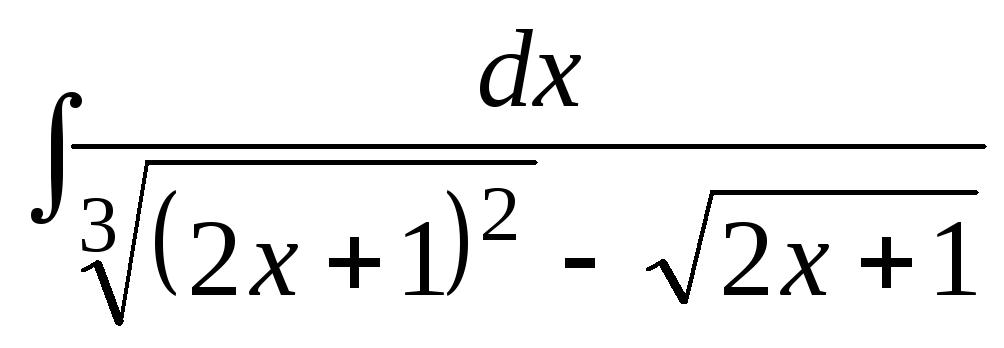 .
.а)
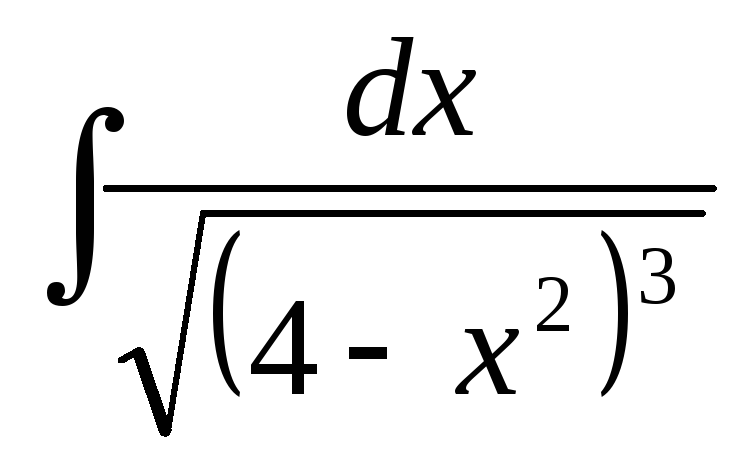 ;
б)
;
б)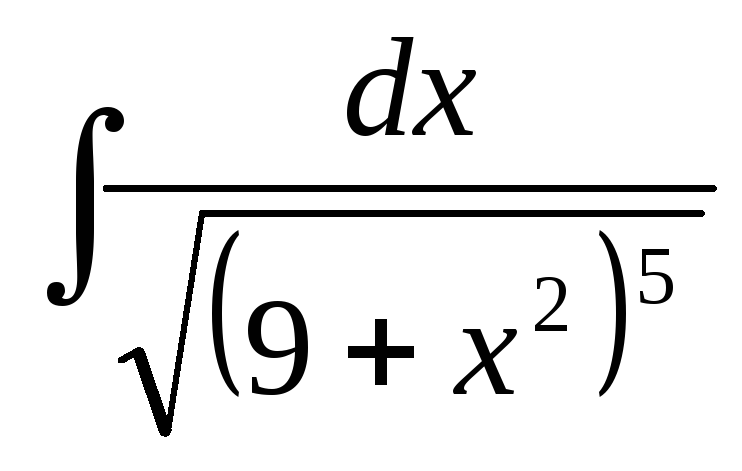 ;
в)
;
в)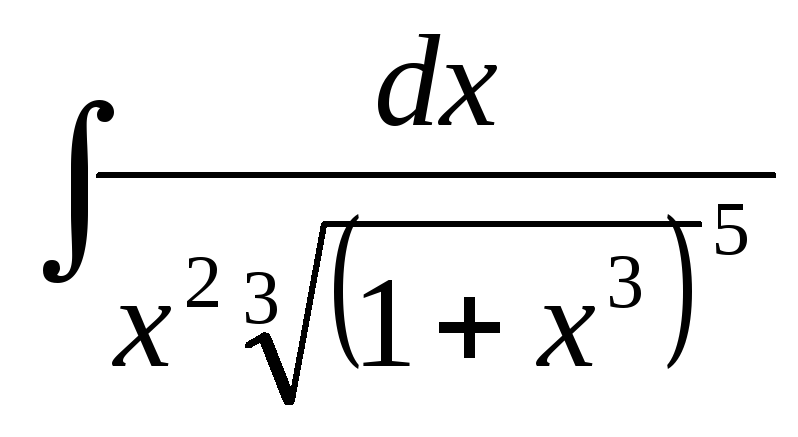 .
.
Задания для самостоятельной работы дома
Вычислите интегралы:
1. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
2. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
3. а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Практическое занятие № 30
Тема занятия «Интегрирование трансцендентных функций»
Цель занятия: формирование умений и навыков вычисления интегралов, содержащие тригонометрические и другие трансцендентные функции.
Организационная форма занятия: практикум.
Компетенции, формируемые на занятии:
способность и готовность анализировать социально-значимые проблемы и процессы, использовать социально-значимые проблемы и процессы, использовать на практике методы гуманитарных, естественнонаучных, медико-биологических и клинических наук в различных видах профессиональной и социальной деятельности (ОК-1).
При формировании этой компетенции в результате изучения дисциплины «Математический анализ» специалист должен знать основные способы интегрирования выражений, содержащих трансцендентные, в том числе тригонометрические функции; уметь интегрировать выражения, содержащие трансцендентные функции.
Вопросы, выносимые на обсуждение
Интегралы вида
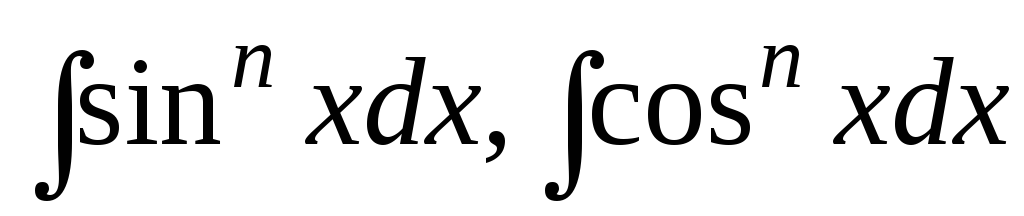 ,
где
,
где
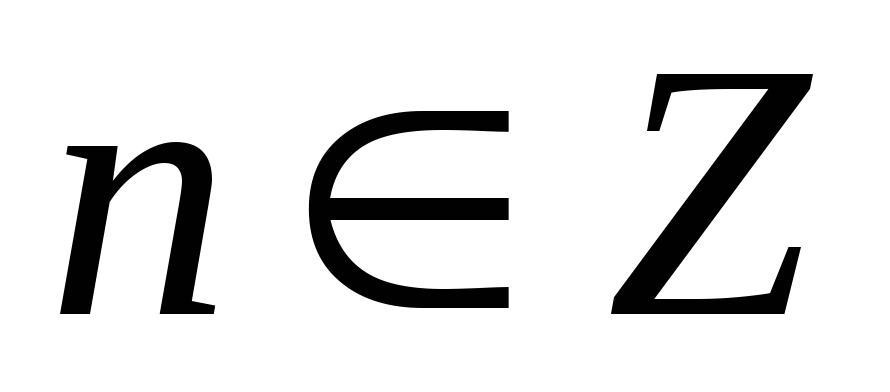 .
.Интегралы вида
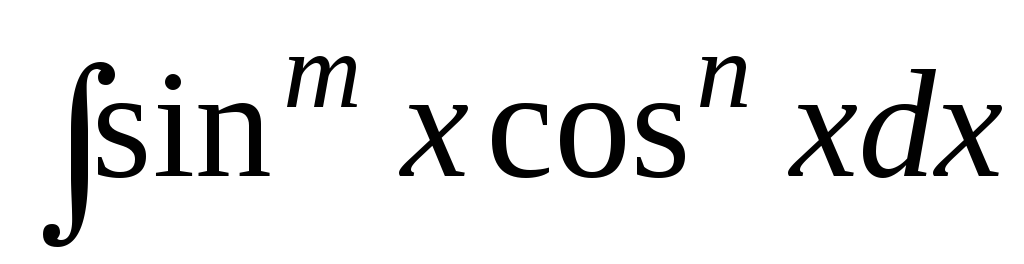 .
.Интегралы вида
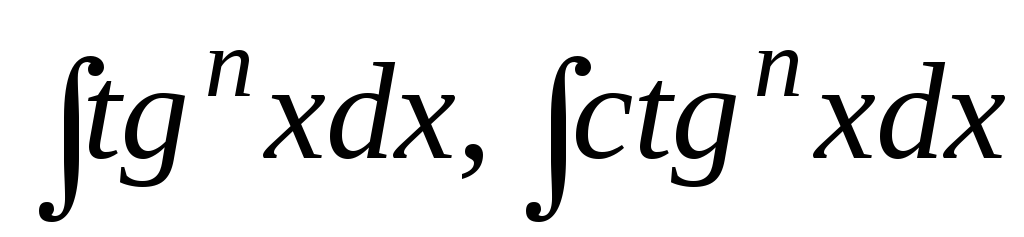 .
.Интегралы от произведения тригонометрических функций.
Интегралы вида
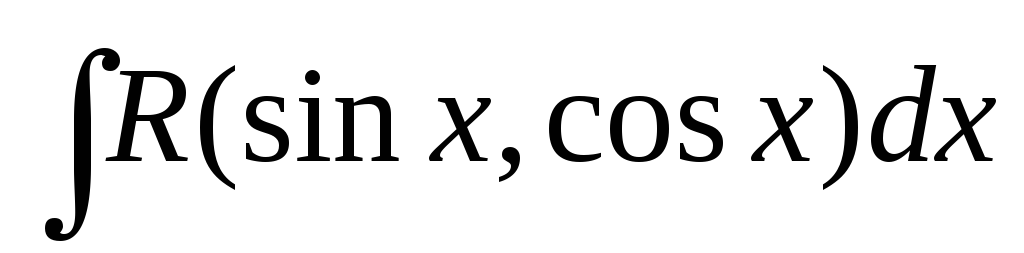 и
и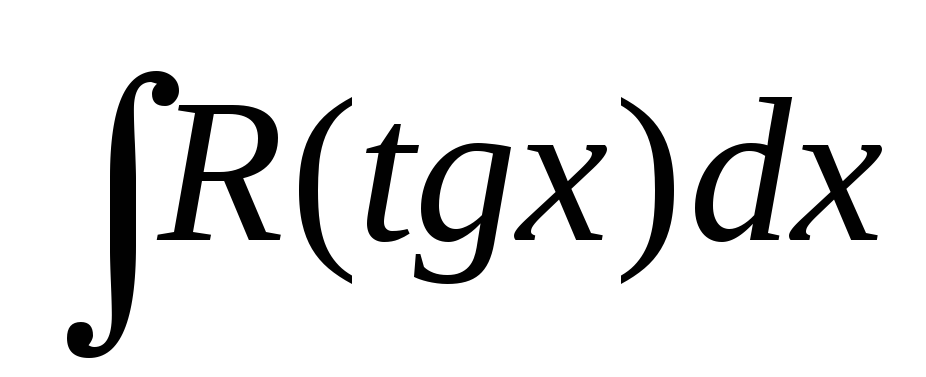 .
.Интегралы вида
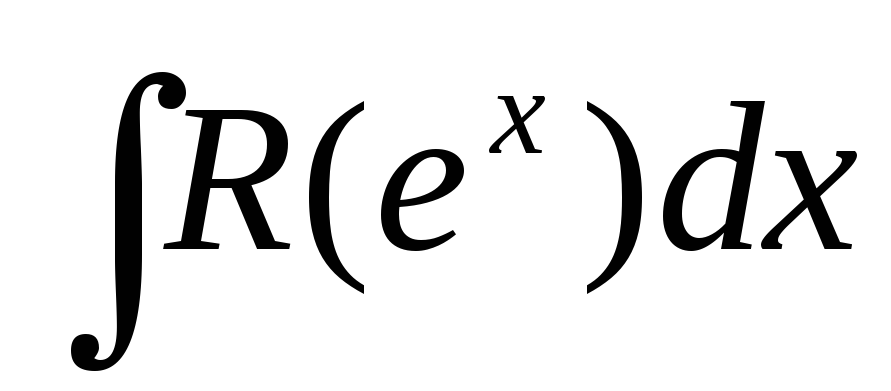 .
.
Методические рекомендации
Для подготовки к занятию дома
Повторите основные формулы тригонометрии, изучаемые в школе.
Прочитайте лекцию, соответствующую теме занятия. Составьте таблицу:
|
Тип интеграла, содержащего тригонометрическую функцию |
Метод вычисления
|
|
|
|
3. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.
На занятии по указанию преподавателя
1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.
2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.
Дома закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.
Рекомендуемая литература
[1] глава 9 п. 9.5.
[2] глава IX §§ 4 - 5.
[3] глава 8 § 41.
[4] часть III занятие 8.
[6] глава 7 § 6.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Вычислите интегралы:
1.
![]()
Решение. Преобразуем
подынтегральную функцию по формуле
![]() получим
получим
![]()
2.
![]()
Решение. Так
как имеем интеграл от нечетной степени
синуса, то отделяем один множитель и
делаем замену
![]() (тогда
(тогда![]() ):
):
![]()
![]()
3.
![]()
Решение. Применяем формулы понижения степени:
![]()
![]()
4.
![]()
Решение.
Подынтегральная
функция есть функция рационально
зависящая от
![]() .
Сделаем подстановку
.
Сделаем подстановку![]() тогда
тогда![]()
![]()
5.
![]()
Решение.
Подынтегральная
функция представляет собой функцию
рационально зависящую от
![]() и
и![]() .
В таком случае применяем подстановку
.
В таком случае применяем подстановку![]() при этом
при этом![]()
Таким образом, получим:
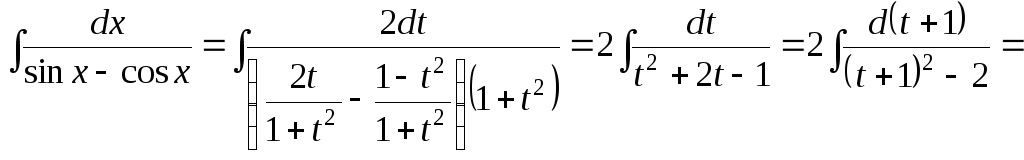
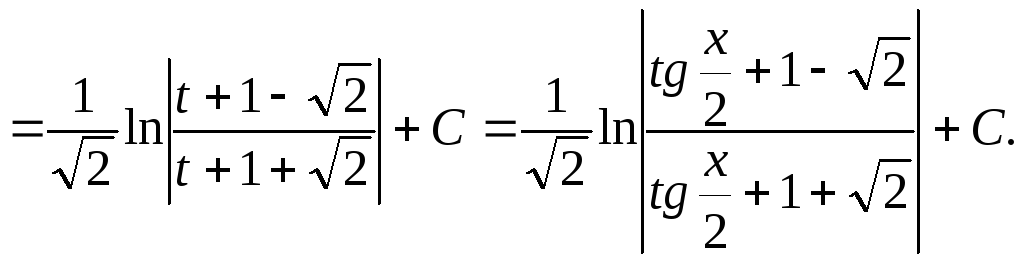
6.
![]()
Решение. Для
нахождения этого интеграла выполним
замену переменной:
![]() ,
тогда
,
тогда![]() .Следовательно,
.Следовательно,
![]()
![]() .
.
Теоретические задания
для развития и контроля владения компетенциями
1. Какие формулы применяются для вычисления следующих интегралов:
а)
![]() где
где![]()
б)
![]() ,
где
,
где![]() и
и![]() положительные целые числа.
положительные целые числа.
2. Расскажите о нахождении интегралов от четной степени синуса или косинуса.
3. Расскажите о нахождении интегралов от нечетной степени синуса или косинуса.
4. Какие случаи
необходимо рассмотреть при нахождении
интегралов вида
![]() .
.
5. Какую замену
следует сделать при нахождении интегралов
вида
![]() ?
?
6. Расскажите о вычислении интегралов от произведения тригонометрических функций.
7. Какой способ
нахождения интегралов вида
![]() ,
,![]() ,
,![]() Вы можете предложить? К какому типу
интегралов они сводятся?
Вы можете предложить? К какому типу
интегралов они сводятся?
8. Какие подстановки удобно применить для взятия следующих интегралов:
а)
![]()
б)
![]()
в)
![]() или
или![]()
г)
![]() или
или![]()
д)
![]() ,
где
,
где![]() - рациональная функция.
- рациональная функция.
9. Приведите примеры «неберущихся» интегралов.
