Лекция 2 Отношение. Способы задания отношений

Исследователя всегда интересуют различные свойства объектов: свойства, относящиеся к отдельным объектам (например, "быть женщиной", "быть белым", "иметь низкую теплопроводность") и свойства, характеризующие связи между несколькими объектами (например, свойства "быть родственниками" и "быть больше" относятся к парам объектов, свойство "находиться между" - к тройкам объектов, свойство "располагаться в вершинах квадрата" - к четверкам объектов).

Такие свойства принято называть отношениями. При этом свойства отдельных объектов называются унарными (одноместными) отношениями, свойства, относящиеся к парам объектов, -бинарными отношениями, свойства, относящиеся к наборам изnобъектов, -n-арными отношениями

Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей теории баз данных. Отношения являются математическим аналогом таблиц.

• Определение Отношения – один из способов задания взаимосвязей между элементами множества.

  • Примеротношений из школьного курса математики являются:

• на множестве целых чисел Z отношения "делится", "делит", "равно", "больше", "меньше", "взаимно просты";

• на множестве прямых пространства отношения "параллельны", "взаимно перпендикулярны", "скрещиваются", "пересекаются", "совпадают";

• на множестве окружностей "пересекаются", "касаются".

Факт принадлежности кортежа (x,y) отношениюR, часто обозначают с помощьюинфикснойформы записи:xR y.

Примерами таких записей из курса математики являются: x>y,a=b,m ||l.

Способы задания отношений

Отношения могут задаваться:

• формулы y = x² +5x - 6- бинарные отношения на множестве действительных чисел;

формула x + y = любовь-бинарное отношение на множестве людей.

• - матричным представлением

• Определение Матрицей бинарного отношения – называется матрица

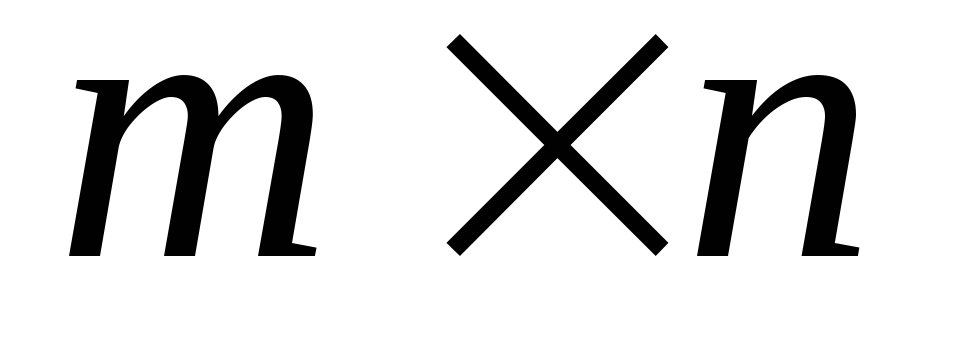
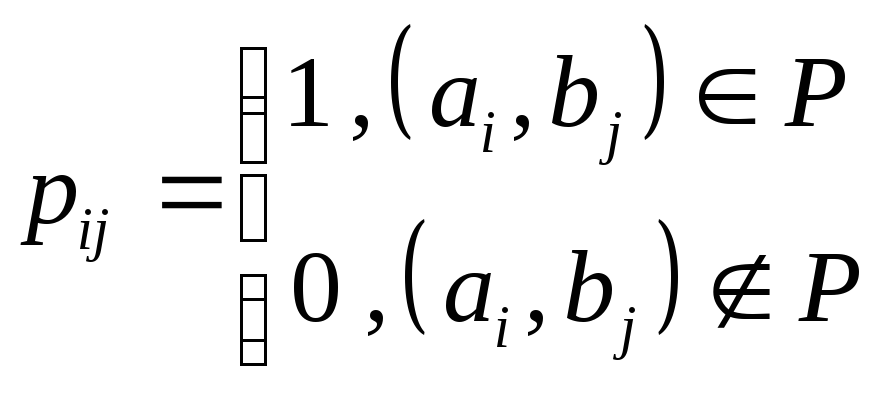
или 1 – если имеет место соотношениеи0если оно отсутствует.

• Пример

задать отношение»быть строго меньше»

матрица бинарного отношения

• графическое представлениеПри таком представлении элементы множестваXизображаются вершинами графа (точками плоскости), а элементы (x,y) отношениядугами (стрелками), соединяющими первую компонентуxотношения со второй компонентойy.

Декартово произведение множеств

В математике достаточно часто приходится иметь дело не только с отдельными элементами какого-либо множества, но и с упорядоченными парами его элементов. Используя две цифры 3 и 5 можно записать 4 числа, важен порядок следования цифр или упорядоченный набор.

• Определение Пустьи- множества. Выражение вида, гдеи, называетсяупорядоченной парой. В общем случае, можно рассматриватьупорядоченную n-куиз элементовилинабориликортеж.

• Определение.Два кортежа равны между собой, т.е. (a₁,...,a_n) = (b₁,...,b_n) тогда и только тогда, когда для любого i выполнено равенство a_i= b_i.

• Пример. (a,a,b)  (a,b,a); (a,2)  (a,2,2).

• Определение Декартовым (прямым) произведением множеств называется множество кортежей вида

декартовым произведениемэтих множеств является совокупность всех возможныхn‑местных элементарных кортежей, у которых на первом месте стоит элемент множества, на втором – элемент множества, ..., а на последнем – элемент множества.

• Примердекартовых произведений.

Для двух множеств X ={a,b},Y= {b,c} декартово произведение

XY = {(a, b), (a, c), (b, b), (b, c)}.

Здесь множество содержит пары элементов, у которых в отличие от множеств порядок строго определен (т.е. их нельзя менять местами). Чтобы отличить (упорядоченные) пары от множеств, их заключают не в фигурные, а в простые круглые скобки.

• Замечание XY  Y X

• Определение Степенью декартового произведенияназывается числоnмножеств, входящих в это декартово произведение.

• Замечание.Если все множестваодинаковы, то используют обозначение

• Замечание термин «декартово произведение» Причем же здесь великий французский математик и философ Рене Декарт? Он изобрел координаты, которые так и называются декартовыми. Множество точек плоскости можно рассматривать как прямое произведение координатных осей.

• Определение Множество элементарных кортежей одной и той же размерностиnназываютмногоместным илиn-местнымотношением.

• Примеротношение "меньше" для множества {1, 2, 3} целых чисел можно представить как множество пар чисел {(1, 2), (1, 3), (2, 3)}

• Теорема Количество всех элементов (т.е. элементарных кортежей) декартова произведения будет равно произведению мощностей всех используемых в этом произведении множеств, т.е.

XY...Z=XY...Z.

• Пример Заданы множестваP = {a,b,c};Q = {a,d,f} иR = {a,b,c, f}, то их декартово произведениеPQRбудет содержать 334=36 элементарных кортежей.

Задача Из города А в город В ведет три дороги, а из города В в город С – 4 дороги. Сколькими способами можно добраться из А в С через В?

Решение

Задача первоначально формулируется не как математическая, а как задача реальной жизни, и поэтому требуется ее переработка в математическую задачу. При этом нужно отделить существенные факторы от несущественных.

Действительно, если при подсчете способов мы будем учитывать время суток, скорость и способ перемещения (пешком, на автомобиле, велосипеде и т. п.), то задача становится чрезвычайно простой, при учете указанных факторов ответ задачи: "Имеется бесконечное множество способов".

Если же отвлечься от всех указанных факторов и под способом попасть из А в С через В понимать упорядоченную пару (дорога, по которой перемещаемся из А в В; дорога, по которой перемещаемся из В в С), то решение задачи можно получить, используя понятие декартова произведения. Обозначим:

АВ – множество дорог, ведущих из А в В;

ВС – множество дорог, ведущих из В в С.

Тогда математическая задача, к которой свелась исходная задача, выглядит так: "Найти число элементов в декартовом произведении АВ×ВС".

|AB×BC| = |AB|·|BC| = 3·4 = 12.

Ответ: 12 способов.

• Замечание Любое множество можно рассматривать как декартовое произведение степени 1, то любое подмножество, как и любое множество, можно считать отношением степени 1.

• ЗамечаниеНетривиальность понятия отношения проявляется, когда степень отношения больше 1.

Ключевыми здесь являются два момента:

1. Все элементы отношения есть однотипные кортежи.

• Пример

отношение, состоит из трех кортежей

{(1, "Иванов", 1000), (2, "Петров", 2000), (3, "Сидоров", 3000)} содержатся данные одного типа.

Множество {(1), (1, 2), (1, 2, 3)}, состоящее из разнотипныхчисловых кортежей. Это множество не является отношением ни в, ни в, ни в.

2. Отношение включает в себя не все возможные кортежи из декартового произведения. Это значит, что для каждого отношения имеется критерий, позволяющий определить, какие кортежи входят в отношение, а какие - нет.

• Определение Кортежпринадлежит отношениютогда и только тогда, когда предикат этого отношенияпринимает значение "истина".