
- •Курс лекций Дискретная математика
- •Оглавление
- •Лекция 1 Элементы теории множеств
- •Множество есть многое, мыслимое нами как единое.
- •Диаграммы Эйлера-Венна
- •Сравнение множеств по числу элементов
- •Операции над множествами
- •Лекция 2 Отношение. Способы задания отношений
- •Декартово произведение множеств
- •Функциональное отношение
- •Бинарные отношения
- •Лекция 3 Основные логические функции
- •Существенные и фиктивные переменные
- •Функции одной переменной
- •Функции двух переменных
- •Законы и теоремы булевой алгебры
- •Лекция 4 Минимизация логических функций
- •Карты Карно
- •Правила минимизации с использованием карт Карно
- •Лекция 5 Замкнутые классы функций
- •Критерий полноты
- •Лекция 6 Графы. Основные термины и понятия
- •Матрица инцидентности и матрица смежности
- •Лекция 7Плоские Графы
- •Лекция 8 Расстояния в графе
- •Алгоритм фронта волны
Правила минимизации с использованием карт Карно
1. В карте Карно группы единиц (для получения ДНФ) и группы нулей (для получения КНФ) необходимо обвести четырехугольными контурами. Внутри контура должны находится только одноименные значения функции. Этот процесс соответствует операции склеивания.
2. Количество клеток внутри контура должно быть целой степенью двойки (1,2,4,8,16...).
3. При проведении контуров крайние строки карты (верхние и нижние, левые и правые), а также угловые клетки, считаются соседними (для карт до 4-х переменных).
4. Каждый контур должен включать максимально возможное количество клеток.
5. Все единицы (нули) в карте (даже одиночные) должны быть охвачены контурами. Любая единица (нуль) может входить в контуры произвольное количество раз.
6. Множество контуров, покрывающих все 1 (0) функции образуют тупиковую ДНФ (КНФ).
7. В элементарной конъюнкции (дизъюнкции), которая соответствует одному контуру, остаются только те переменные, значение которых не изменяется внутри обведенного контура.
8. Переменные булевой функции входят в элементарную коньюнкцию (для значений функции 1) без инверсии, если их значение на соответствующих координатах равно 1 и с инверсией - если 0.
Для значений булевой функции, равных 0, записываются элементарные дизьюнкции, куда переменные входят без инверсии, если их значение на соответствующих координатах равно 0 и с инверсией - если 1. Тупиковая форма записи функции, полученная при минимизации по карте Карно, используется при проектировании логических устройств так же, как и полученная методом алгебраической минимизации
Пример в карте Карно четырех переменных можно выделить группу из четырех клеток в первом столбце, группу из четырех угловых клеток и группу из двух соседних клеток в нижней строке (табл.).
|
|
|
Таблица | |||
|
х |
00 |
01 |
11 |
10 | |
|
х3х4 |
00 |
1 |
0 |
0 |
1 |
|
01 |
1 |
0 |
0 |
0 | |
|
11 |
1 |
0 |
0 |
0 | |
|
10 |
1 |
0 |
1 |
1 | |
В результате минимизированная функция представляет собой сумму трех произведений, соответствующих отдельным группам:
![]()
Рассмотрим возможные варианты расположения единиц в карте Карно.
1)Рядом стоящие элементарные квадраты, в которых записаны "1", образуют прямоугольники 4x2. Рядом стоящими считаем как непосредственно рядом расположенные квадраты, так и квадраты, находящиеся в строках 1 и 4 и столбцах 1 и 4.
Каждому прямоугольнику 4x2 в минимальной форме будет соответствовать произведение из одного сомножителя. Пусть после заполнения получили таблицу:
|
x3x4 x1x2 |
00 |
01 |
11 |
10 | ||||
|
00
|
1 |
0 |
1 |
1 |
1 |
3 |
1 |
2 |
|
01
|
1 |
4 |
1 |
5 |
0 |
7 |
0 |
6 |
|
11 |
1 |
12 |
1 |
13 |
0 |
15 |
0 |
14 |
|
10 |
1 |
8 |
1 |
9 |
1 |
11 |
1 |
10 |
В данном случае можно
составить 2 прямоугольника 4X2,
целиком состоящих из "1". На первом
прямоугольнике x1,
принимает значение 0 и 1, x2=0,1
X4=0,1
X3=0
поэтому в минимальной форме будет
присутствовать произведение, состоящие
из
![]() ,
т.к. только
,
т.к. только![]() обращается
в 1 на всем наборе. Аналогично для второго
прямоугольника находим
обращается
в 1 на всем наборе. Аналогично для второго
прямоугольника находим![]() .
.
Окончательно:
![]()
Здесь ограничились поиском только двух прямоугольников, т.к. они включили в себя все "№" таблицы.
2) Рядом стоящие элементарные квадраты, в которых записаны "1" образуют прямоугольники 2x1.
В этом случае в минимальной форме будут присутствовать произведения из трех сомножителей.
|
x3x4 x1x2 |
00 |
01 |
11 |
10 | ||||
|
00
|
1 |
0 |
0 |
1 |
0 |
3 |
1 |
2 |
|
01
|
0 |
4 |
1 |
5 |
0 |
7 |
0 |
6 |
|
11 |
0 |
12 |
1 |
13 |
0 |
15 |
0 |
14 |
|
10 |
0 |
8 |
0 |
9 |
0 |
11 |
1 |
10 |
Здесь можно выделить 3 прямоугольника: 0-2; 5-13; 2-10;
На первом наборе: X1=0, X2=0, X3=0 и 1, X4=0.
Поэтому
имеем:
![]() .
.
На втором
наборе: ![]() ,на
третьем:
,на
третьем: ![]()
Окончательно
получаем:
![]()
3) Из элементарных квадратов, в которых записаны “1”, составить вышеописанные фигуры нельзя. В этом случае квадратам, в которых записаны “1” будут соответствовать произведения из четырех сомножителей.
|
x3x4 x1x2 |
00 |
01 |
11 |
10 | ||||
|
00
|
1 |
0 |
0 |
1 |
0 |
3 |
0 |
2 |
|
01
|
0 |
4 |
0 |
5 |
1 |
7 |
0 |
6 |
|
11 |
0 |
12 |
0 |
13 |
0 |
15 |
0 |
14 |
|
10 |
0 |
8 |
1 |
9 |
0 |
11 |
0 |
10 |
Здесь имеем:
![]()
ПримерРассмотрим минимизацию булевой функции трех переменных
f ( 1,3,5,6,7 ) = 1
Решение
Построим минимальную ДНФ
Функция 3-х переменных
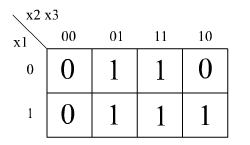 исходная
функция f ( 1,3,5,6,7 ) = 1
исходная
функция f ( 1,3,5,6,7 ) = 1
1.шаг

![]()
2. шаг
Построим минимальную КНФ
1. шаг

2 шаг
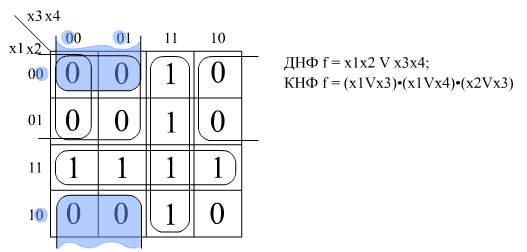
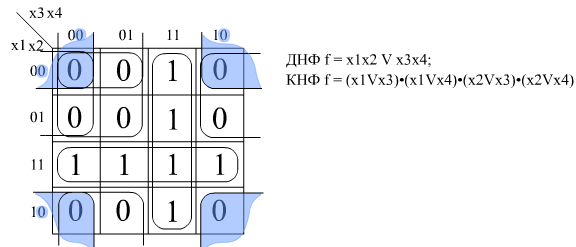
Пример Рассмотрим минимизацию булевой функции четырех переменных
f ( 3,7,11,12,13,14,15 ) = 1.
Функция 4-х переменных

КНФ
 1 шаг
1 шаг
2. шаг

шаг
шаг

 1х2
1х2
