Карты Карно
Компактной и очень удобной формой записи логической функции, используемой наряду с таблицей истинности, является карта Карно (по таблицам значений этих функций). Данный метод был разработан в 1953 г. американским ученым Морисом Карно.
Карта Карноявляется специальной компактной формой таблицы истинности, которая позволяет не только представить функцию, но и минимизировать ее.
Карта Карно, или диаграмма Вейча, — это таблица, имеющая ячейки для всех возможных наборов функции. Количество клеток в карте Карно равно количеству строк в таблице истинности. Каждая клетка соответствует одной строке таблицы. Комбинации входных переменных распределяются по двум сторонам прямоугольника, а соответствующие значения функции в клетках таблицы, находящихся на пересечении строк и столбцов, соответствующих выбранным состояниям переменных.
Карта Карно является координатным способом представления булевых функций. При этом способе задания таблица истинности функции представляется в виде координатной карты состояний, которая содержит 2n клеток (по числу входных наборов булевой функции n переменных).
Переменные функции разбиваются на две группы так, что одна группа определяет координаты столбца карты, а другая - координаты строки. При такoм способе построения каждая клетка определяется значениями переменных, соответствующих определенному двоичному набору. Внутри каждой клетки карты Карно ставится значение функции на данном наборе. Переменные в строках и столбцах располагаются так, чтобы соседние клетки карты Карно различались только в одном разряде переменных, т.е были соседними.
Определение Соседними считаются клетки карты, отличающиеся значениями только одной входной переменной.
Поэтому значения переменных в столбцах и в строках карты образуют соседний код Грея. Такой способ представления очень удобен для наглядности при минимизации булевых функций. Карта Карно 4 переменных, с точки зрения определения "соседства" переменных, геометрически представляет собой пространственную фигуру тор или, проще говоря, "бублик".
Отметим, что метод карт Карно применим к минимизации булевых функций до 6-ти переменных (до 4 переменных на плоскости) и до 6 - в трехмерной интерпретации.
Карта Карно для функции двух переменных содержит четыре клетки и имеет форму квадрата (табл. 1). Два возможных значения первой переменной х1отражаются обычно на верхней стороне квадрата, значения второй переменнойх2– на левой стороне.
Если какой-то из этих наборов в СДНФ записи функции присутствует, то в соответствующей клетке карты Карно ставится «1». Если какого-то набора в полученной функции нет, то в соответствующей клетке карты Карно ставится «0».
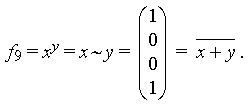
Пример. Составить карту Карно для функцииэквивалентность
В карте Карно двух переменных (эквивалентность) (табл. 1) каждая клетка имеет две соседние.
|
Таблица
1 х1 0 1 х2 0 1 0 1 0 1 | |||||||||||||||
Карта Карно для функции трех переменных состоит из 8 клеток и имеет обычно 2 строки и четыре столбца (табл. 2).
|
Таблица
2 х1
х2 00 01 11 10 х3 0 0 0 1 0 1 0 1 1 1 | |||||||||||||||||||||||
На верхней стороне прямоугольника каждому столбцу ставится в соответствие одна комбинация входных переменных х1их2. Причем, при переходе от каждого столбца к соседнему имеет право измениться только одна переменная, а первый и последний столбцы карты также считаются соседними. В карте трех переменных каждая клетка имеет три соседние.
Пример. Занесём в карту Карно для четырёх переменных следующую логическую функцию:
.
|
|
Таблица 3 | ||||
|
х1х2 |
00 |
01 |
11 |
10 | |
|
х3х4 |
00 |
1 |
0 |
0 |
1 |
|
01 |
1 |
0 |
0 |
0 | |
|
11 |
1 |
0 |
0 |
0 | |
|
10 |
1 |
0 |
1 |
1 | |
В карте Карно для функции четырех переменных 16 клеток. Две переменные хlих2располагаются наверху квадрата, а две другиех3их4– слева (табл. 3). В отличие от предыдущего случая здесь каждой строчке таблицы соответствует определенная комбинация двух переменныхх3их4.
При переходе от каждой строки к соседней меняется только одна переменная, а первая и последняя строки карты, так же как и крайние столбцы, считаются соседними. Каждая клетка карты имеет четыре соседние клетки.
Обобщая карту Карно для y=f(x1,x2,x3,x4) можно представить в виде таблицы 4x4.
|
x3x4 x1x2 |
00 |
01 |
11 |
10 | ||||
|
00
|
(0,0,0,0) |
0 |
(0,0,0,1) |
1 |
(0,0,1,1) |
3 |
(0,0,1,0) |
2 |
|
01
|
(0,1,0,0) |
4 |
(0,1,0,1) |
5 |
(0,1,1,1) |
7 |
(0,1,1,0) |
6 |
|
11 |
(1,1,0,0) |
12 |
(1,1,0,1) |
13 |
(1,1,1,1) |
15 |
(1,1,1,0) |
14 |
|
10 |
(1,0,0,0) |
8 |
(1,0,0,1) |
9 |
(1,0,1,1) |
11 |
(1,0,1,0) |
10 |
Верхняя строка и левый столбец являются координатными и определяют номер квадрата (например, если x1,x2,x3,x4=(0,1,1,1), то номер квадрата = 7). В квадраты записываются единичные значения минимизируемой булевой функции f(x1,x2,x3,x4).
Если в карте Карно встречаются группы из 2-х, 4-х, 8-ми и т.д. соседних ячеек, содержащих единицы, которые можно выделить контуром в виде прямоугольника, то такая группа может быть описана одним логическим произведением. В это произведение входят только неизменные для всех ячеек данной группы переменные.
Склеивание осуществляется между теми наборами, которые записаны в виде «1» в соседних клетках карты (соседних по вертикали или горизонтали). При склеивания в карте Карно соседние «1» могут быть покрыты квадратами со стороной, кратной двум.