chisl_meth / Лаб 6 QR-алгоритм, метод итераций / QR-алгоритм

QR-разложение

Для нахождения собственных значений матрицы, используя QR-алгоритм, необходимо предварительно использовать QR-разложение, которое представляет собой разложение матрицы в виде , где Q – ортогональная матрица; R – верхнетреугольная матрица. Существует ряд методов для реализации QR-разложения: процесс Грама – Шмидта; преобразование Хаусхолдера; вращение Гивенса.

Процесс Грама – Шмидта

Рассмотрим процесс Грама – Шмидта для некоторой матрицы . Определим проекцию

,

тогда

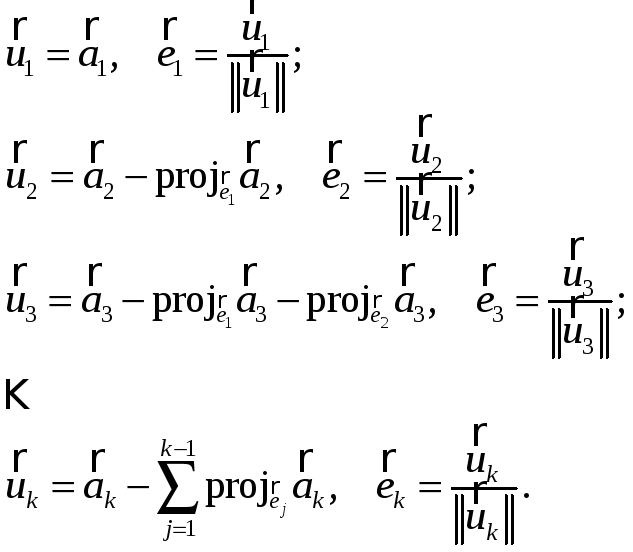
Матрицы Q и R будем формировать следующим образом:

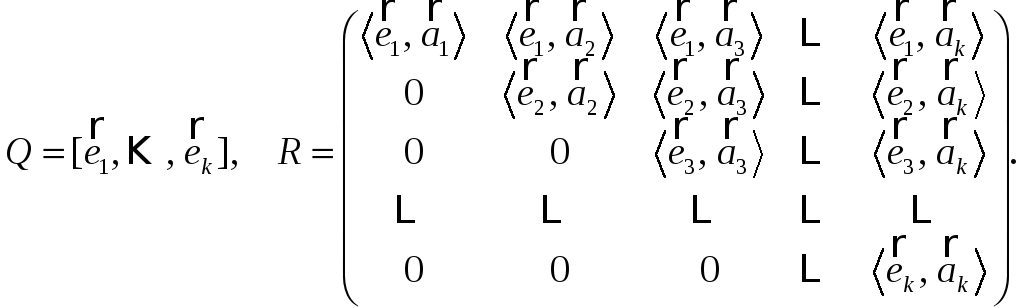
Матрицу R можно найти и другим путем. Преобразуем выражение следующим образом: . Произведение есть единичная матрица. Отсюда следует, что зная матрицу Q, мы можем определить матрицу R

.

Преобразование Хаусхолдера

Идея преобразования Хаусхолдера – осуществить ряд преобразований, которые позволят сделать нулевыми элементы столбцов ниже главной диагонали. Пусть имеется матрица:

.

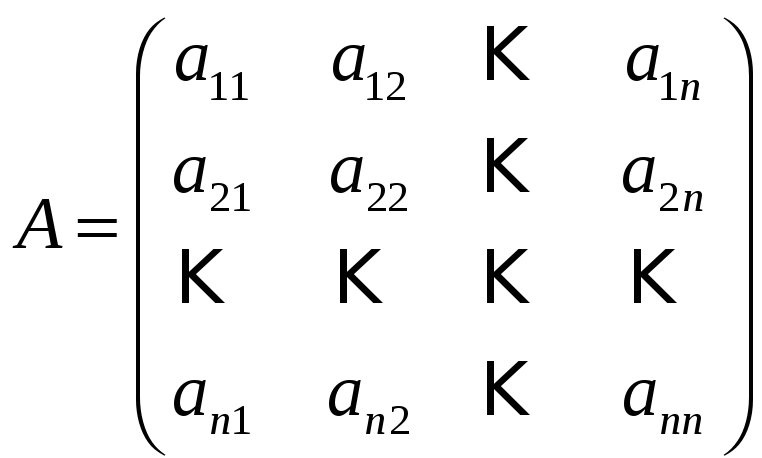Возьмем первый столбец и вычислим с его помощью вектор

,

который мы используем для построения матрицы Хаусхолдера:

.

Если умножить матрицу на исходную , то в первом столбце полученной матрицы ниже главной диагонали будут нули. Запишем минор матрицы :

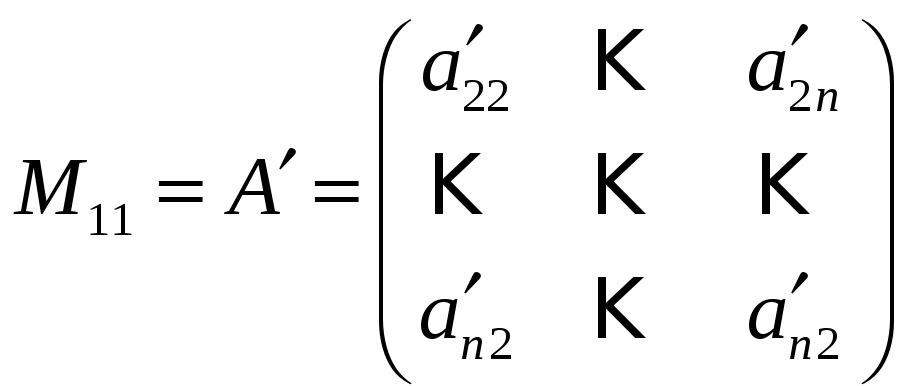
и проделаем для этой матрицы операции записанные выше, т. е. , тогда

, ,

и т. д.

Матрицы разложения могут быть получены как

, .

Пример

.

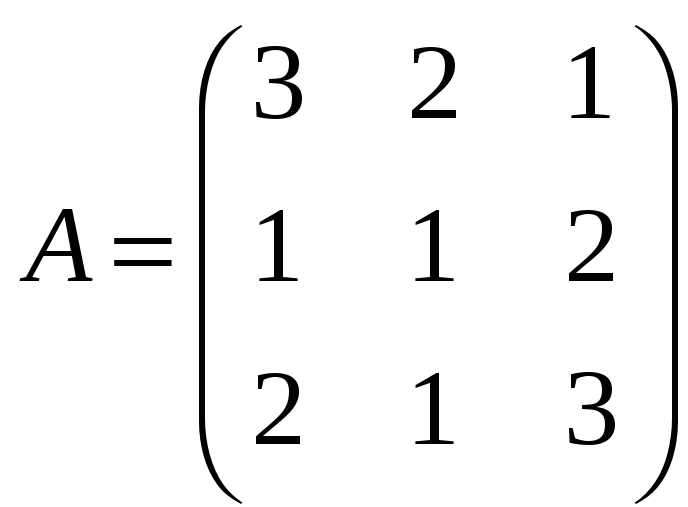Запишем первый столбец матрицы , тогда

,

Матрица будет иметь вид

Используя второй столбец минора , строим вектор и

,

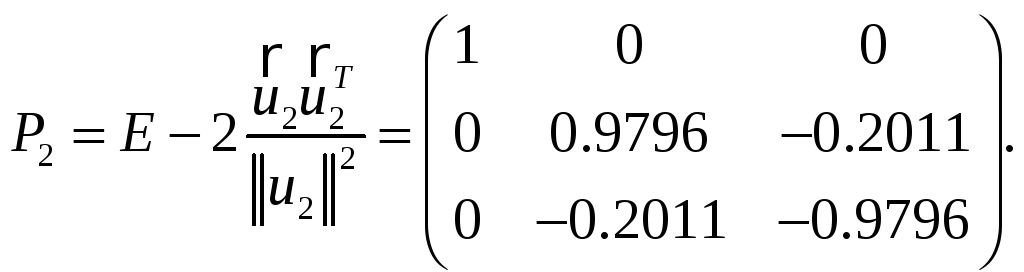
Произведение матрицы на дает матрицу , у которой элементы ниже главной диагонали будут равны нулю. Это и есть искомая матрица R:

,

а матрица Q примет вид

.

QR-алгоритм

Теперь мы можем осуществить QR-разложение матрицы одним из приведенных способов. Тогда для последовательности матриц и запишем процесс, который представляет собой QR-алгоритм.

1. Задаем и .

2. Вычисляем , затем находим QR-разложение как .

3. Определяем и представляем в виде и т. д.

…

m. Находим , после чего записываем

На некотором шаге m матрица становится треугольной или почти треугольной, поэтому ее собственные числа будут находиться на главной диагонали. Чем больше m, тем ближе собственные числа матрицы к собственным числам матрицы A.

Пример. Используя QR-алгоритм, вычислить собственные числа матрицы

.

Шаг 1.

Шаг 2.

Шаг 3.

…

Шаг 12.

Приближенные значения собственных чисел находятся на главной диагонали и равны