
chisl_meth / Лаб 6 QR-алгоритм, метод итераций / QR-A
.pdf
QR METHOD |
1 12 |
Next: PROBLEMS 6.3 Up: NUMERICAL CALCULATION OF EIGENVALUES Previous: PROBLEMS 6.2
QR METHOD
The basis of the  method for calculating the eigenvalues of
method for calculating the eigenvalues of 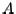 is the fact that an
is the fact that an 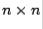 real matrix can be written as
real matrix can be written as
factorization of 
where 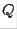 is orthogonal and
is orthogonal and  is upper triangular. The method is efficient for the calculation of all eigenvalues of a matrix.
is upper triangular. The method is efficient for the calculation of all eigenvalues of a matrix.
The construction of |
and |
proceeds as follows. Matrices |
 are constructed so that
are constructed so that 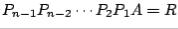 is upper
is upper
triangular. These matrices can be chosen as orthogonal matrices and are called householder matrices. Since the 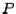 's are orthogonal, the stability of the eigenvalue problem will not be worsened (this is proved in numerical analysis texts). If we let
's are orthogonal, the stability of the eigenvalue problem will not be worsened (this is proved in numerical analysis texts). If we let
then we have 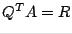 and
and
We discuss the construction of the 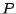 's presently. First, we state how the
's presently. First, we state how the 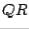 factorization of
factorization of 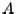 is used to find eigenvalues of
is used to find eigenvalues of 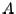 . We define
. We define
sequences of matrices |
and |
by this process:
Step 1.
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |
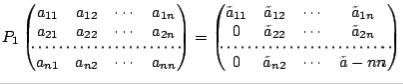
QR METHOD |
2 12 |
Set  , and
, and  .
.
Step 2.
First set  ; then factor
; then factor  as
as 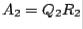 (
(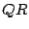 factorization of
factorization of  ).
).
Step 3.
First, set  ; then factor
; then factor  as
as  (
(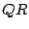 factorization of
factorization of  ).
).
Step 4.
Set 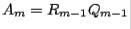 ; then factor
; then factor  as
as  (
(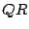 factorization of
factorization of  ).
).
At the 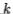 th step, a matrix
th step, a matrix  is found, first, by using
is found, first, by using 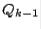 and
and  from the previous step; second,
from the previous step; second, 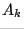 is factored into
is factored into 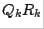 . Thus a
. Thus a  factorization takes place at each step. Matrix
factorization takes place at each step. Matrix 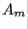 will tend toward a triangular or nearly triangular form. Thus the eigenvalues of
will tend toward a triangular or nearly triangular form. Thus the eigenvalues of 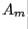 will be
will be
easy to calculate. The importance is that if the eigenvalues can be ordered as  , then the following is true:
, then the following is true:
As  increases the eigenvalues of
increases the eigenvalues of  approach the eigenvalues of
approach the eigenvalues of  .
.
The proof of this fact is well beyond the scope of this book. Before applying the  algorithm to some examples, we discuss the
algorithm to some examples, we discuss the 
factorization of a matrix 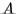 .
.
The idea in  factorization is to first find
factorization is to first find 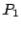 which, when multiplied on the left of
which, when multiplied on the left of  , will produce zeros below
, will produce zeros below  . That is, we want
. That is, we want
After this is done, we find  which will produce
which will produce
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |

QR METHOD |
3 12 |
The process is continued until we have
The problem is to find the  matrices. It turns out that the matrices
matrices. It turns out that the matrices 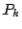
can be chosen as orthogonal matrices. In fact, the construction proceeds as follows.
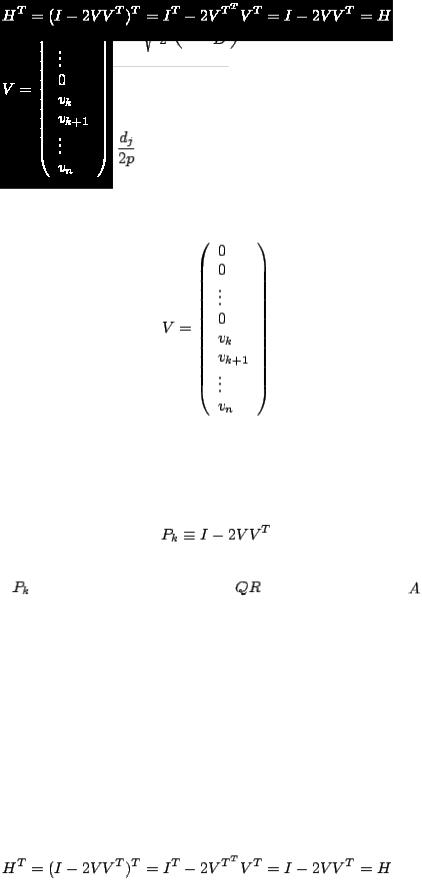
To construct 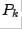 :
:
1. Pull column 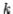 out of the matrix
out of the matrix 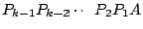 (just
(just 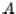 if
if  ):
):
2. Normalize this column vector, and call the new vector
3.Set 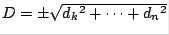 (choose + if
(choose + if 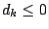 ).
).
4.Set 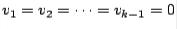 . Also set
. Also set
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |
QR METHOD |
4 12 |
and
for
5. Write
Note that  . 6. For the matrix
. 6. For the matrix
The matrix |
will work for finding a |
factorization of . These |
matrices, because of their form, are called householder matrices. It can be shown that householder matrices are orthogonal.
Definition 6.3.1 A householder matrix is any matrix of the form 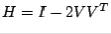 , where
, where  .
.
Theorem 6.3.1 Householder matrices are orthogonal.
Proof. We show that  . By definition, then,
. By definition, then, 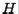 would be orthogonal. First we note that
would be orthogonal. First we note that 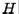 is symmetric:
is symmetric:
Now
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |

QR METHOD |
5 12 |
Example 1 Find a 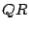 factorization of
factorization of
keeping four digits to the right of the decimal point.
Solution The first column normalized is
The ``diagonal'' element is 0.8165. We want zeros below it. First we calculate 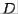 :
:
The minus sign was chosen since 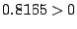 . Now we set
. Now we set
Thus
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |

QR METHOD |
6 12 |
Multiply  by
by  ; we obtain
; we obtain
To construct 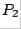 , we look at column 2 of
, we look at column 2 of 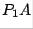 :
:
Normalized, this is
In this case |
. The minus sign is chosen |
since |
. We set |
|
and |
So |
|
 Actually we obtain 0.0008. Because of rounding, we called this zero.
Actually we obtain 0.0008. Because of rounding, we called this zero.
Therefore,
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |
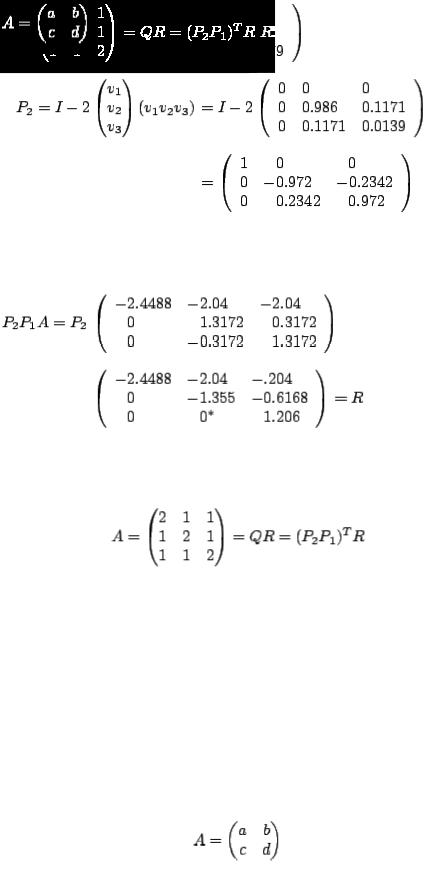
QR METHOD |
7 12 |
and we have
Finally,
Therefore,
From the example just calculated, we see that finding the 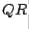 factorization for a
factorization for a  matrix is tedious by hand. A computer, of course, is necessary to find
matrix is tedious by hand. A computer, of course, is necessary to find  factorizations and, therefore, to use the
factorizations and, therefore, to use the 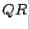 method for finding eigenvalues.
method for finding eigenvalues.
For a  matrix, only one householder matrix must be found, so we consider the
matrix, only one householder matrix must be found, so we consider the  factorization for a general
factorization for a general  matrix
matrix
The first column, normalized, is
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |

QR METHOD |
8 12 |
 Actually 0.0001. Because of rounding we call this zero.
Actually 0.0001. Because of rounding we call this zero.
Now 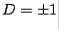 , so we can write
, so we can write  sign
sign  , where sign
, where sign 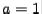 if
if 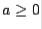 and sign
and sign  if
if 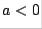 .
.
 sign
sign
where sign 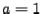 if
if 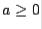 and sign
and sign  if
if  . Since
. Since  , we have
, we have  sign
sign 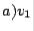 . For
. For 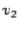 we have
we have
Therefore,
snf
Since  is symmetric,
is symmetric, 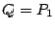 .
.
Example 2 Find a  factorization of
factorization of
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |
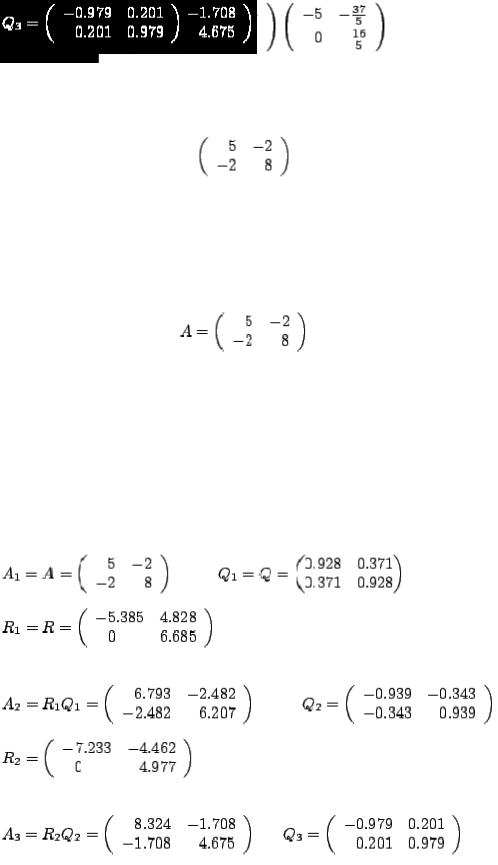
QR METHOD |
9 12 |
Solution Using the formulas as above, we find that
Using the formulas for the 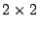 case, we now calculate the eigenvalues of
case, we now calculate the eigenvalues of
by the 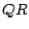 method.
method.
Example 3 Use the 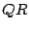 method to calculate the eigenvalues of
method to calculate the eigenvalues of
(The true eigenvalues are 4 and 9.)
Solution We use the formulas for the  case each time we need a
case each time we need a 
factorization. The calculated matrices are listed below (rounded); after step 3, only 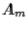 is listed.
is listed.
Step 1:
Step 2:
Step 3:
Step 4:
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |

QR METHOD |
10 12 |
Step 5:
Step 6:
Step 12:
Approximate eigenvalues are on the diagonal.
In Example 3, 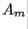 appeared to be converging to a diagonal matrix; of
appeared to be converging to a diagonal matrix; of
course, the diagonal elements are the approximate eigenvalues. This illustrates the following important result.
Theorem 6.3.2 Let 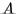 be a real
be a real 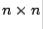 matrix with eigenvalues satisfying
matrix with eigenvalues satisfying
Then matrices  in the
in the  method will converge to an upper triangular matrix with diagonal entries
method will converge to an upper triangular matrix with diagonal entries 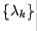 ,
,  . If
. If 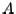 is symmetric, matrices
is symmetric, matrices  converge to a diagonal matrix with the eigenvalues on the diagonal.
converge to a diagonal matrix with the eigenvalues on the diagonal.
If the hypotheses of Theorem 6.3.2 are not satisfied by 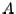 , the
, the
method may fail. If the difference in the magnitudes of the eigenvalues is small, convergence of the 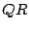 method can be slow.
method can be slow.
Example 4 Applying the  method to attempt calculation of eigenvalues of
method to attempt calculation of eigenvalues of
http://distance-ed.math.tamu.edu/Math640/chapter6/node6.html |
2006/3/20 |
