
решение задач по ОТУ
.docx-
По логарифмическим частотным функциям определить запас устойчивости по усилению в системе, передаточная функция которой в разомкнутом состоянии
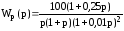
РЕШЕНИЕ:
Из выражения для передаточной функции следует, что система состоит из последовательно соединенных интегратора, корректирующего звена с отставанием по фазе и двух одинаковых инерционных звеньев.
По определению
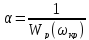 ,
,
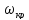 - частота, на которой
- частота, на которой
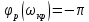 .
.
Интегратор создает
фазовый сдвиг-
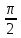 на всех частотах. Два одинаковых
инерционных звена создадут фазовый
сдвиг -
на всех частотах. Два одинаковых
инерционных звена создадут фазовый
сдвиг -
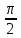 на частоте
на частоте
 ,
на которой каждое звено создает фазовый
сдвиг -
,
на которой каждое звено создает фазовый
сдвиг -
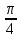 .
Частота сопряжения
.
Частота сопряжения
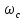 определяется
из соотношения
определяется
из соотношения
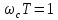 ,
где Т=0.01, тогда
,
где Т=0.01, тогда
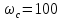 с-1.
с-1.
Определим фазовый
сдвиг на частоте
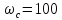 с-1,
создаваемый корректирующими звеньями:
с-1,
создаваемый корректирующими звеньями:
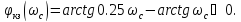
Т.к.
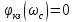 ,
следовательно
,
следовательно
 .
.
Тогда
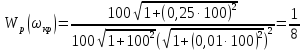 ,
= 8.
,
= 8.
11. По логарифмическим частотным функциям определить запас устойчивости по усилению в системе, передаточная функция которой в разомкнутом состоянии
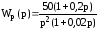 .
.
РЕШЕНИЕ:
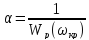
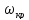 - частота, на которой
- частота, на которой
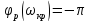 .
.
Система состоит из 2-х интеграторов и корректирующего звена с опережением по фазе.
2 интегратора создадут фазовый сдвиг –π.
Для определения
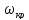 составим уравнение:
составим уравнение:
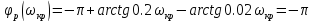 .
.
(в уравнении приведена сумма ФЧХ звеньев, входящих в систему – двух интеграторов и корректирующего звена).
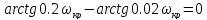
Это уравнение
справедливо при
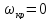 и
и
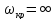 .
Физический смысл имеет второй ответ,
тогда
.
Физический смысл имеет второй ответ,
тогда
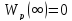 ,
,
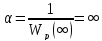 .
.
Ответ: = .
-
Передаточная функция разомкнутой системы
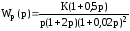 .
.
Определить коэффициент усиления К в системе, при котором запас устойчивости по усилению = 10.
Из выражения передаточной функции следует, что система состоит из интегратора, корректирующего звена с отставанием по фазе и двух одинаковых инерционных звеньев, соединенных последовательно.
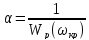
 - частота, на которой
- частота, на которой
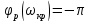 .
.
Интегратор создает
фазовый сдвиг-
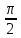 на всех частотах. Два одинаковых
инерционных звена создадут фазовый
сдвиг -
на всех частотах. Два одинаковых
инерционных звена создадут фазовый
сдвиг -
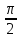 на частоте
на частоте
 ,
на которой каждое звено создает фазовый
сдвиг -
,
на которой каждое звено создает фазовый
сдвиг -
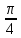 .
Частота сопряжения
.
Частота сопряжения
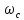 определяется
из соотношения
определяется
из соотношения
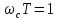 ,
где Т=0.02, тогда
,
где Т=0.02, тогда
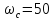 с-1.
с-1.
Определим фазовый
сдвиг на частоте
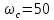 с-1,
создаваемый корректирующими звеньями:
с-1,
создаваемый корректирующими звеньями:
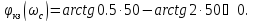
Т.к.
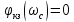 ,
следовательно
,
следовательно
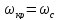 .
.
Тогда
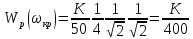 ,
=
,
=
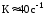 .
.
13. Передаточная функция замкнутой системы
 .
.
Определить импульсную характеристику (t) замкнутой системы.
РЕШЕНИЕ:
По определению
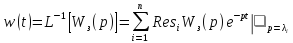 ,
,
где
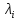 – полюсы
– полюсы
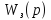 или корни характеристического уравнения.
или корни характеристического уравнения.
Представим
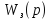 в виде
в виде
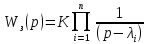 и получим
и получим
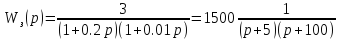 ,
,
откуда
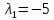 ,
,
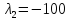 .
.
Формула для вычетов при некратных полюсах:
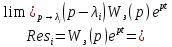 ,
,
тогда
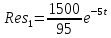 ,
,
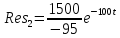 .
.
Импульсная характеристика имеет вид:
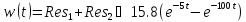
Ответ: (t) = 15,8 (е -5t - e -100t).
14. Передаточная функция разомкнутой системы
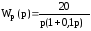 .
.
Найти импульсную характеристику (t) замкнутой системы.
РЕШЕНИЕ:
По определению
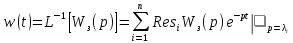 ,
,
где
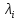 – полюсы
– полюсы
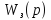 или корни характеристического уравнения.
или корни характеристического уравнения.
По условию дана передаточная функция разомкнутой системы. Запишем передаточную функцию для замкнутой системы:
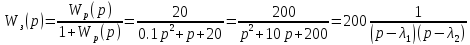 ;
;
Корни
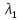 и
и
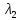 найдем из характеристического уравнения
найдем из характеристического уравнения
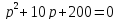 ,
,
откуда
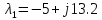 ,
,
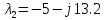 .
.
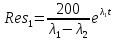 ,
,
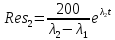
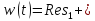
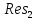 =15.1
=15.1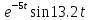
Ответ: (t) = 15,1е -5t sin13,2t.
15. Передаточная функция замкнутой системы
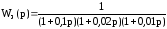 .
.
Определить выходной сигнал в установившемся режиме при управляющем воздействии x(t) = 1(t) и указать порядок астатизма системы.
РЕШЕНИЕ:
См. Задачу №3.
Сигнал ошибки
е=х-ууст=1-1=0,
следовательно
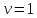 .
.
Ответ: yуст = 1; = 1.
-
Передаточная функция замкнутой системы
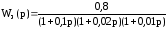 .
.
Определить выходной сигнал в установившемся режиме при входном сигнале x(t) = 1(t) и указать порядок астатизма системы.
См. задачу №3.
Сигнал ошибки
е=х-ууст=1-0,8=0,2,
следовательно
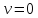 .
.
Ответ: yуст = 0,8; = 0.
-
Передаточная функция системы в разомкнутом состоянии
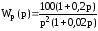 .
.
Определить выходной сигнал в установившемся режиме в замкнутой системе при входном воздействии x(t) = 10sin5t.
РЕШЕНИЕ:
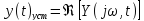 ,
где
,
где
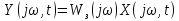
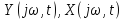 - комплексные
входной и выходной сигналы;
- комплексные
входной и выходной сигналы;
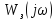 - комплексный коэффициент передачи
замкнутой системы.
- комплексный коэффициент передачи
замкнутой системы.
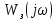 - комплексный
коэффициент передачи замкнутой системы.
- комплексный
коэффициент передачи замкнутой системы.
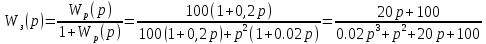
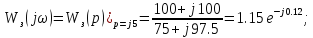
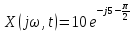 ;
;
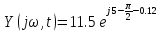
Ответ: y(t)уст = 11,5sin(5t - 0,12).
-
Передаточная функция разомкнутой системы
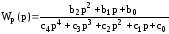 .
.
Каковы условия получения указанного порядка астатизма замкнутой системы
= 0, = 1, = 2 ?
РЕШЕНИЕ:
Порядок астатизма
замкнутой системы определяется из
выражения для передаточной функции,
представленному в виде:
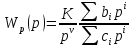 ,
где
,
где
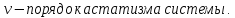
Из данного выражения видно, что = 0 при с0 0, = 1 при с0 = 0,
= 2 при с0 = с1 = 0.
-
Передаточная функция замкнутой системы
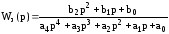 .
.
Каковы условия получения указанного порядка астатизма системы
= 0, = 1, = 2 ?
РЕШЕНИЕ:
Выразим
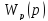 через передаточную функцию
через передаточную функцию
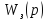 из равенства
из равенства
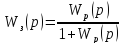 ,
откуда
,
откуда
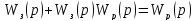
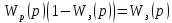 ,
,
Тогда
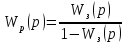 ,
т.к.
,
т.к.
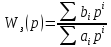 ,
тогда
,
тогда
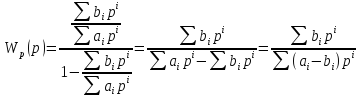 .
.
Представим
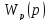 в виде
в виде
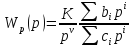 .
.
Сравнивая выражения
для передаточной функции, видим, что
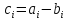 .
.
= 0 при b0 a0 ,
= 1 при b0 = a0, b1 a1 ,
= 2 при b0 = ao, b1 = a1, b2 a2 .
20. Передаточная функция ошибки системы
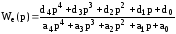 .
.
Каковы условия получения указанного порядка астатизма системы
= 0, = 1, = 2 ?
РЕШЕНИЕ:
Выразим
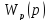 через передаточную функцию
через передаточную функцию
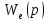 из равенства
из равенства
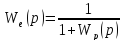 .
Откуда
.
Откуда
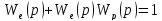 .
.
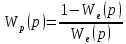 .
Т.к.
.
Т.к.
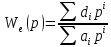 ,
тогда
,
тогда
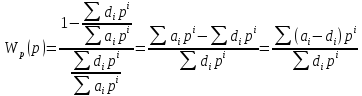 .
.
Представим
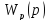 в виде
в виде
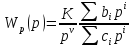 .
Сравнивая выражение для
.
Сравнивая выражение для
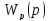 ,
видим, что
,
видим, что
 .
.
Тогда = 0 при при d0 0,
= 1 при d0 = 0,
= 2 при d0 = d1 = 0.
-
Передаточная функция разомкнутой системы
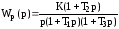 .
.
Найти ошибку в замкнутой системе при входном воздействии
x(t) = a01(t) + a11(t)t .
РЕШЕНИЕ:
По определению
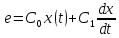 .
.
Представим
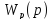 в виде
в виде
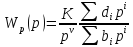 .
.
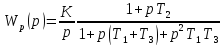 ,
откуда
,
откуда
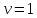 ,
,
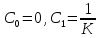 .
.
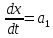 ,
,
тогда
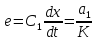
Ответ:
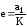 .
.
22. Передаточная функция разомкнутой системы
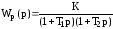 .
.
Найти ошибку в замкнутой системе при входном воздействии
x(t) =a11(t)t .
РЕШЕНИЕ:
По определению
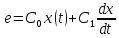 .
.
Представим
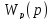 в виде
в виде
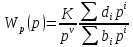 .
.
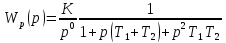 ,
откуда
,
откуда
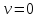 ,
,
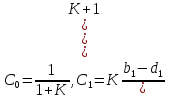 ,
,
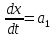 ,
,
тогда
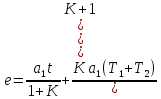
Ответ:
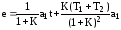 .
.
23. Передаточная функция замкнутой системы
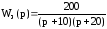 .
.
Определить характеристическую матрицу при последовательной схеме описания системы в пространстве состояний.

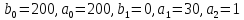 .
.
Матрица системы имеет вид:
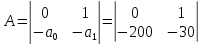 .
.
Характеристическая матрица:
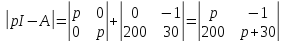 .
.
Ответ:
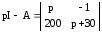 .
.
-
Матрица, обратная характеристической, для системы имеет вид:
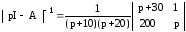 .
.
Определить элементы фундаментальной матрицы, используя следующие соотношения, полученные из формулы для вычетов
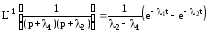 ,
,
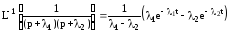 .
.
РЕШЕНИЕ:
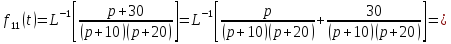
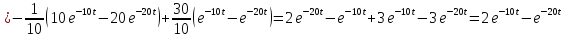
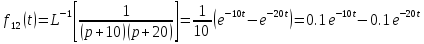
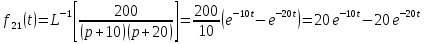
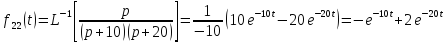
Ответы:
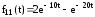 ,
,
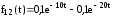 ,
,
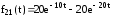 ,
,
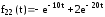 .
.
25. Передаточная функция замкнутой системы
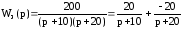 .
.
Определить матрицу системы, вектор управления, наблюдения и описать ее по параллельной схеме описания системы в пространстве состояний.
РЕШЕНИЕ:
Представим
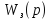 в виде
в виде
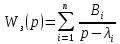 .
Здесь n=2,
.
Здесь n=2,
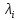 - полюсы системы,
- полюсы системы,
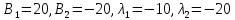 .
.
Тогда матрица
системы
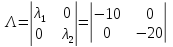
Вектор управления
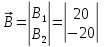
Ответы:
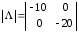 ,
,
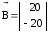 ,
,
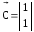 .
.
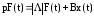
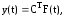 где Т - символ
транспонирования. (стр. 20-22)
где Т - символ
транспонирования. (стр. 20-22)
-
На рисунке изображена структурная схема нелинейной системы
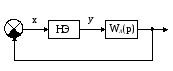
Функция нелинейного элемента (НЭ) имеет вид
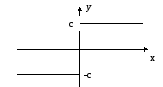
Нелинейный элемент - это идеальный ограничитель с порогами ограничения С. Линейная часть системы состоит из последовательно соединенных усилителя и четырех одинаковых инерционных звеньев с передаточной функцией
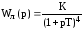 .
.
Определить амплитуду Ак и частоту к автоколебаний в этой системе.
Ответы:
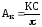 ;
;
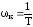 .
.
27. На рисунке изображена структурная схема нелинейной системы
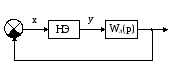
Функция нелинейного элемента (НЭ) имеет вид
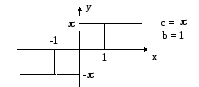
Линейная часть системы представляет собой последовательное соединение усилителя и четырех одинаковых инерционных звеньев, передаточная функция которой описывается выражением
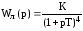 .
.
Определить, при превышении какого коэффициента усиления усилителя К в этой системе возникнут автоколебания. При каком К система загенерирует без НЭ?
Ответы: К > 2; К > 4.
28. Системная функция цифрового дифференциатора имеет вид W(z) = 1 - z -1. Используя стандартное Z - преобразование, получите выражение для АЧХ цифрового дифференциатора.
Ответ: W()
= 2sin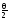 ,
,
где = Тд , - угловая частота, Тд - период дискретизации.
Подобная задача приведена в учебнике на стр.100.
