
Выполнение курсовой работы Расчетная часть курсовой работы
Теория:
Передаточная функция
Передаточной функцией системы называется отношение изображения по Лапласу выходного сигнала к изображению по Лапласу входного сигнала, т.е.:

Инерционное звено
В инерционном или апериодическом звене выходной сигнал связан с входным соотношением
 ,
,
откуда
Y(p) = k X(p) - p T Y(p) ,
где Т - постоянная времени звена.
Передаточная функция инерционного звена:
 .
.
Если в схеме на рис.1 вместо R2 конденсатор С, а вместо R1 включить резистор R (рис.1), то в соответствии с приведенными на рис.1 обозначениями получим
Рис. 1. Схема инерционного звена:

u = u1
+ u2
, u1
= i R ,
 .
.
Тогда
U(p) =
U1(p)
+ U2(p)
= I(p) R +
 I(p) .
I(p) .
По определению
W(p) =
 .
.
После сокращения числителя и знаменателя на рС получим
W(p) =
 ,
,
где Т = RC - постоянная времени.
Интегратор
В интеграторе выходной сигнал связан с входным соотношением:
 ,
,
откуда
 где
где , ТИ
- постоянная времени интегратора.
, ТИ
- постоянная времени интегратора.
Передаточная функция интегратора:
 .
.
Корректирующее звено с отставанием по фазе
Схема корректирующего звена с отставанием по фазе приведена на рис. 1. Сигналом u2(t) в этом звене является напряжение на цепи R2 С.
По определению
 ,
,
где
 .
.
С учетом

имеем
 .
.
Удобнее это выражение представить в виде:
 ,
,
где Т = R2
C,
 .
.
Рис. 1. Схема корректирующего звена с отставанием по фазе:

Дифференцирующая цепь
Схема дифференцирующей цепи приведена ниже. Изображение по Лапласу напряжений на элементах схемы UС(p) = ZС(p) I(p), тогда с учетом (4.4) получим:

По определению
 .
.
Умножив числитель и знаменатель на рС, получим:
 ,
,
где T = RC - постоянная времени RC-цепи.
Этой передаточной функции соответствует дифференциальное уравнение, следующее из соотношения:
 ,
,
откуда
 .
.
Здесь y(t)=uR(t) , x(t)=u(t).
АЧХ и ФЧХ
Амплитудно-частотной
характеристикой (АЧХ) называется
зависимость модуля ККП от частоты

Фазочастотной
характеристикой (ФЧХ) называется
зависимость аргумента ККП от частоты

Логарифмические АЧХ и ФЧХ
Логарифмическая АЧХ (ЛАЧХ) определяется выражением

При этом по оси абсцисс в линейном масштабе откладывается не частота , а логарифм частоты. Чаще всего используются логарифмы по основанию 2, log2 или по основанию 10, lg. В первом случае шкала называется октавной, а во втором случае декадной.
Логарифмическая ФЧХ (ЛФЧХ) строится так: по оси ординат откладывается значение (), а по оси абсцисс в линейном масштабе откладывается логарифм частот log2 или lg.
Решение:
Так как в исходную часть схемы следящей системы входят четыре инерционных звена и интегратор, а гарантированно-устойчивой замкнутая система будет только при двух инерционных звеньях, поэтому дополнительно понадобится два корректирующих звена. Для упрощения расчетов возьмём эти звенья с одинаковыми параметрами, передаточная функция которых имеет вид:

необходимо определить kкз, T1 и T2.
С учетом корректирующих звеньев передаточная функция разомкнутой системы имеет вид:


Коэффициенты ошибок по положению, скорости и ускорению равны:

 ,
,
где
b1 – коэффициент при первой степени p знаменателя;
d1 – коэффициент при первой степени p числителя.


Получим первое уравнение из системы 2-х уравнений, решив которую найдем T1 и T2

Второе соотношение определим из ЛАЧХ разомкнутой системы. Сначала определим запас устойчивости по фазе:

Затем найдем частоту среза разомкнутой системы:

Проверяем условие:

Если это условие выполняется, то до частоты среза ЛАЧХ разомкнутой системы будет определятся только интегратором и двумя корректирующими звеньями с отставанием по фазе.

1 – ЛАЧХ интегратора,
2 – ЛАЧХ одного корректирующего звена
(от 0 до
 наклон
наклон ),
),
3 – ЛАЧХ двух корректирующих звеньев
(от 0 до
 наклон
наклон ),
),
4 – ЛАЧХ системы (от 0 до
 наклон
наклон ,
от
,
от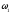 до
до наклон
наклон ,
,
от
 до
до наклон
наклон ).
).
До частоты 1 ЛАЧХ определяется интегратором:
 ,
,
на участке (1, 2):






 .
.
Второе соотношение имеет вид:
 .
.
Решаем систему уравнений:
 ,
,
решив данную систему, получим следующие значения:

Если T1 – T2 > 0, то имеем корректирующие звенья с отставанием по фазе.
Первое корректирующие звено включим после фазового детектора, в состав этого звена включим усилитель.

Необходимо рассчитать параметры этой схемы:

В этой формуле неизвестным является R, поэтому полагаем R = 1 ÷ 5 кОм. Выбираем R = 1 кОм.
Отсюда,


