
decision_4132
.docЗадача 1
Даны координаты вершин пирамиды ABCD.
__ ^ __
Найти: 1) |AB|; 2) (AB;AC); 3) пр AB;
AC;
4) площадь грани ABC; 5) уравнение грани ABC
6) уравнение ребра AD; 7) угол между ребром AD и
гранью ABC;
8) смешанное произведение (AB, AC, AD) и V - объём пирамиды ABCD;
9) уравнение высоты,опущенной из вершины D на грань ABC и
ее длину; 10) уравнение плоскости, проходящей через точку D
параллельно грани ABC.
A(2;0;8);
B(0;2;0); C(3;2;8); D(0;5;0)![]()
1) |AB|;
![]()
2) (AB;AC);

3) пр AB
AC;
![]()
4) площадь грани ABC;

5) уравнение грани ABC

6) уравнение ребра AD;

7) угол между ребром AD и гранью ABC;
![]()

8) смешанное произведение (AB, AC, AD) и V - объём пирамиды ABCD;

9) уравнение высоты,опущенной из вершины D на грань ABC и ее длину;

![]()
10) уравнение плоскости, проходящей через точку D параллельно грани ABC.

Задача 2
На координатной плоскости задан треугольник ABC
координатами своих вершин. Требуется найти :
1) уравнение стороны AB, 2) уравнение высоты CD
и вычислить ее длину, 3) уравнение медианы BM,
угол q между высотой CD и медианой BM
A(3;2); B(7;8); C(8;2)
Уравнение стороны АB

2) уравнение высоты CD и вычислить ее длину,
k1*k2=-1
k2=-1/ k1= -1/2.5 = -0,4
y-2=-0.4(x-8)
y-2=-0.4x-3.2
y=-0.4x-1.2 – уравнение высоты.
![]()
3) уравнение медианы BM,
Xм= (Xa+Xc)/2 = (3+8)/2=5.5
Yм= (Ya+Yc)/2 = (2+2)/2=2
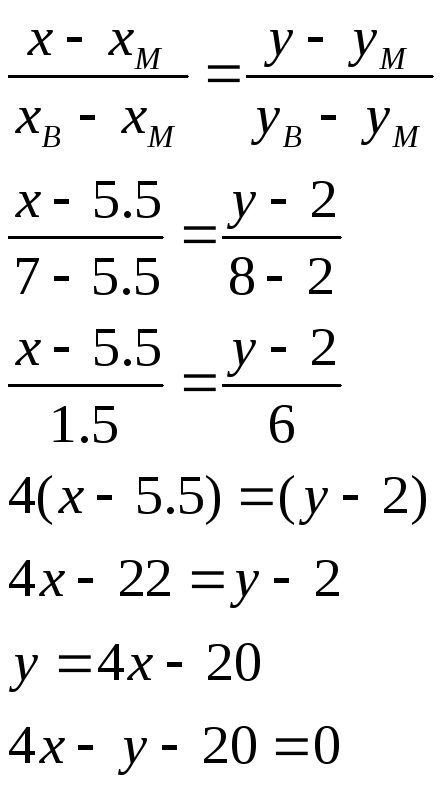
угол q между высотой CD и медианой BM

Задача 3
Выполнить следующие действия над комплексными числами
u 3_ 5
1) u + v; 2) u - v; 3) u ∙ v; 4) ───; 5) √v; 6) v
v
u = 8 + i ; v = -4 - i
1) u + v = 8 + i – 4 – i = 4
2) u – v = 8 + i + 4 + i = 12 +2i
3) u ∙ v = (8 + i) ∙(- 4 – i) = - (8 + i) ∙(4 + i) = - (32 + 4i + 8i + i2)=
=- (32 + 4i + 8i - 1) = - (31 + 12i)= - 31 – 12i
4)
![]()
5)

6)

Задача 4
Найти пределы функций, не пользуясь правилом Лопиталя
1)
3 2
-x + 16x - 62x - 16
lim ─────────────────────
x─>8 3 2
6x - 39x - 76x + 32

2)
3 2
-4x - x + 2
lim ──────────────────
x─>OO 3 2
-2x + x - 8x – 2

3)
______________ _____________
/ 2 / 2
√ 6x - 10x + 68 - √ 9x - 7x + 62
lim ─────────────────────────────────────
x─>1 ________________ ____________
/ 2 / 2
√ - 9x + 3x + 42 - √ x - 4x + 39

4)
_____________
/ 2
√ 4x - 3x - 9
lim ───────────────
x─>OO 7x + 8

5)
2
┌ 2 ┐3x + x - 5
│ - 2x + 6x - 6 │
lim │ ─────────────── │
x─>OO │ 2 │
│ - 2x + 6x + 9 │
└ ┘

6)
lim (3x + 2)( Ln(8x - 6) - Ln(8x - 3))
x─>OO

Задача 5
Найти производную y' данной функции
5 3 3 5 6 7
y = 5[ sin(x )∙arctg(x )] + [ 5cos(x )] + 4Ln[ 8ctg(x )]
![]()

Задача 6
Исследовать методами дифференциального исчисления
и построить график функции
2
y = ( - 3x + 6x + 3)∙exp(x - 1)
Решение.
1) Найдем область определения, интервалы непрерывности и точки разрыва функции.
Функция определена на всей числовой оси
В каждой точке области определения функция непрерывна.
2) Выясним четность, нечетность и периодичность функции.
![]()
Следовательно, функция не является ни четной ни нечетной.
Функция непериодична, т.к. y(x±T)y(x), где Т– некоторое действительное число.
3) Найдем асимптоты графика функции (вертикальные, горизонтальные, наклонные).
А) Вертикальные асимптоты – нет , так как нет точек разрыва.
Б) горизонтальные асимптоты.
Для нахождения горизонтальной асимптоты нужно найти предел функции при х→∞, раскрывая неопределенность вида ∞/∞. Если существует конечный предел.
![]()
то прямая y=b определяемая уравнением, есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем пределы

График имеет горизонтальную асимптоту y=0 слева.
В) наклонная асимптота
наклонная асимптота – y=kx+b
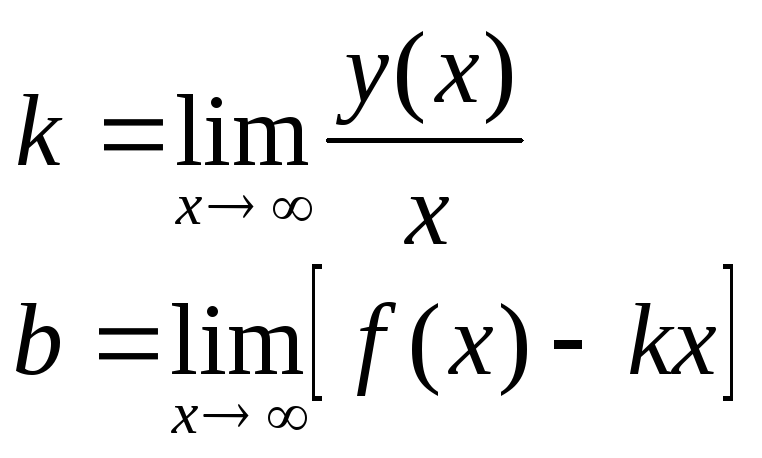
Найдем оба указанных предела для заданной функции

Т.е. наклонная асимптота превращается в горизонтальную.
Наклонных асимптот нет.
4) Найдем интервалы возрастания и убывания функции, точки экстремума и экстремумы. Находим сначала первую производную функции:
![]()
Критическими точками первого рода являются точки, в которых
y’(x)=0 или
![]() ,
следовательно (х2 –3)=0, т.е. х=
,
следовательно (х2 –3)=0, т.е. х=![]()
Критические точки х=![]() разбивают
числовую ось ОХ на 3 интервала монотонности
функции. По знаку производной в этих
интервалах определяем интервалы
возрастания и убывания функции, точки
экстремума и экстремумы функции.
Полученные данные заносим в таблицу.
разбивают
числовую ось ОХ на 3 интервала монотонности
функции. По знаку производной в этих
интервалах определяем интервалы
возрастания и убывания функции, точки
экстремума и экстремумы функции.
Полученные данные заносим в таблицу.
|
Х |
(-∞; |
|
( |
|
( |
|
y’(x) |
+ |
0 |
- |
0 |
- |
|
y(x) |
Убывать |
-1,067 - минимум |
Возрастать |
9,133 максимум |
Убывать |
5) Найдем интервалы выпуклости и вогнутости графика функции, точки перегиба.
Находим сначала вторую производную функции:
![]()
Критическими точками второго рода
являются точки в которых y’’=0
![]() =0;
х = -3; х= 1.
=0;
х = -3; х= 1.
Критические точки разбивают числовую ость ОХ на 3 интервала, в которых по знаку второй производной определяем интервалы выпуклости и вогнутости графика и ординату точки перегиба. Полученные данные заносим в таблицу.
|
Х |
(-∞;-3) |
-3 |
(-3;1) |
1 |
(1; +∞) |
|
y’(x) |
- |
0 |
+ |
0 |
- |
|
y(x) |
Выпукла |
-0,769 |
Вогнута |
6 |
выпукла |
Точка перегиба функции (-3; - 0,769) и (1; -6)
7) Используя результаты исследования, строим график функции

Задача 7
Найти наибольшее и наименьшее значения функции
6 4 2
f(x) = 4x - 9x + 6x + 4 на [-2 ; 3]
Задание 3. Найти наибольшее и наименьшее значения функций у=f(x) на отрезке [a,b]
y= 4x6 – 9x4+6x2+4; x [-2;3]
Решение.
Используем правило для нахождения наибольшего и наименьшего значений непрерывной функции у=f(x) на отрезке [a,b]
1) найти критические точки из уравнения , лежащие внутри отрезка [a,b], и вычислить значения функции в этих точках (не выясняя будет ли в них экстремум функции и какого вида);
2) Вычислить значения функции на концах отрезка, т.е. значения f(a) и f(b)
3) Сравнить значения функции в критических точках и на концах отрезка: самое большое из них будет наибольшим значением унаиб, а самое меньшее – наименьшим значением унаим функции y=f(x) на всем данном отрезке.
Находим производную y’= 24x5 –36х3+12x = 12 x( 2x4 –3х2+1)
Находим критические точки, принадлежащие отрезку [-2; 3] из уравнения:
12 x( 2x4
–3х2+1) = 0 , x=
0;
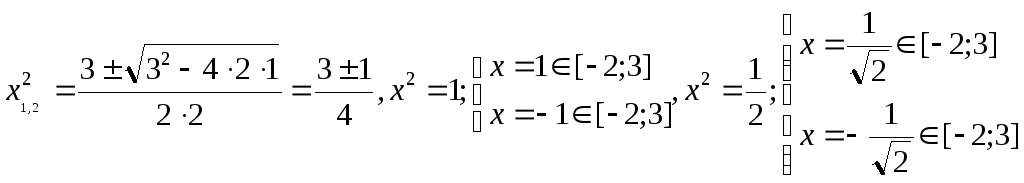
Вычисляем значения функции в критических точках:
y= 4x6 – 9x4+6x2+4

Вычисляем значения функции на концах отрезка:
![]()
Сравнивая все вычисленные значений функции заключаем:
![]()
Ответ
![]()
