4. Кодер

Кодер обеспечивает представление квантованных по уровню отсчетов сообщения помехоустойчивым двоичным кодом. Эта операция осуществляется в два этапа. На первом из них производится примитивное кодирование: каждый уровень квантованного сообщения представляется комбинацией k-разрядного равномерного двоичного кода . На втором этапе из них формируются комбинации помехоустойчивого кода.

Предполагается, что в данной системе используется широко известный код Хэмминга (7,4), исправляющий одиночные ошибки. Комбинации, принадлежащие данному коду, содержат информационных и3 проверочных символа. Общее число кодовых символов в одной кодовой комбинации7.

Кодовые символы при использовании такого кода определяются следующим образом.

Первые 4 символа совпадают с информационными:

(4.1}

а остальные (проверочные) символы определяются из следующих соотношений:

(4.2)

Требуется выполнить следующее.

4.1.Определить число разрядов примитивного кода, необходимое для кодирования всех уровней квантованного сообщения.

4.2.Записать комбинацию примитивного двоичного кода, соответствующую передаче -го уровня, считая, что она представляет собой запись числав двоичной системе счисления.

4.3.Разбить полученную последовательность на четырёхразрядные комбинации информационных символов. (При необходимости дополнить двоичное число нулями в старших (левых) разрядах).

4.4. Построить порождающую матрицу используемого кода в соответствии с соотношениями (4.1) и (4.2).

4.5.Используя порождающую матрицу выразить все =16 разрешённые кодовые комбинации через строки порождающей матрицы.

4.6.Используя результаты п.п. 4.3. - 4.5., закодировать передаваемую информационную последовательность. При этом кодовые комбинации разделяются символами (;)

Методические указания.

Выполнение этого пункта требует знаний по разделу «Основы теории кодирования»: [1], глава 7 ,[2], п.5.1, 5.3, 5.4; [3], п.5.1, 5.2; [4], п.4.1, 4.2; [5]. Для более углубленного изучения этих вопросов рекомендуется.

Число разрядов примитивного кода , необходимое для кодирования уровней квантованного сообщения, определяется из очевидного условия, что общее число всех возможных комбинаций из двоичных разрядов должно быть равно .Запись комбинации примитивного двоичного кода, соответствующей передаче -го уровня, поясним на примере. Пусть , . Представим число 217 в двоичной системе счисления:

Коэффициенты этого представления образуют 8 информационных символов комбинации примитивного кода:

1	1	0	1	1	0	0	1

Порождающей матрицей линейного блокового кода (где - общее число символов в комбинации, - количество информационных символов в комбинации) может служить прямоугольная матрица размера , строками которой являются любые ненулевых линейно-независимых разрешённых кодовых комбинаций. В канонической форме строками такой матрицы являются кодовые комбинации, информационные составляющие которых образуют единичную матрицу, а проверочные символы определяются в соответствии с соотношением (4.2):

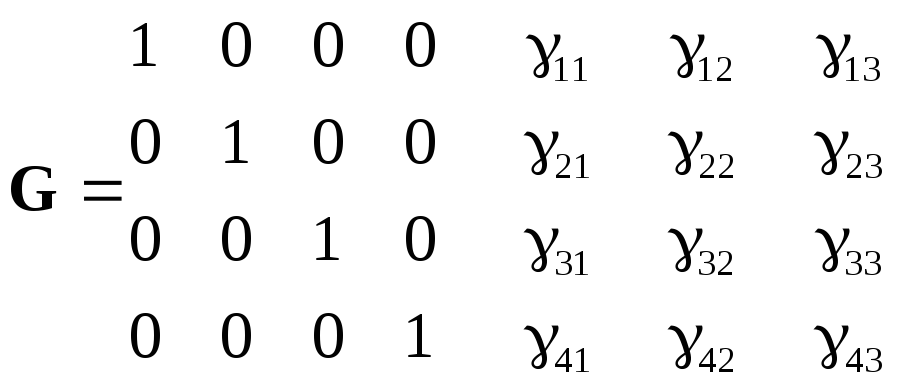(4.3)

Любую разрешённую кодовую комбинацию можно получить путём суммирования по модулю 2 двух или более строк порождающей матрицы. Нулевая комбинация, которая является необходимым элементом любого линейного кода, получается суммированием любой строки матрицы «сама с собой».