Программа работы

1. Собрать схему рис. 4.1

2. Изменяя частоту источника питания (10–12 значений, включая f_р), исследовать режимы работы цепи. Результаты измерений занести в табл. 4.1.

3. Используя данные измерений, рассчитать указанные в табл. 4.1 величины:

– активное сопротивление цепи

;

(4.3)

– индуктивное сопротивление катушки

;

(4.4)

– емкостное сопротивление конденсатора

;

(4.5)

– реактивное сопротивление цепи

;

(4.6)

– индуктивное напряжение

;

(4.7)

– емкостное напряжение

;

(4.8)

– величину угла 

.

(4.9)

Примечание. Параметры схем замещения катушки индуктивности (R_LиL) и конденсатора (R_CиС) рассчитаны в лабораторной работе № 3.

4. По данным таблицы 4.1 построить частотные характеристики цепи рис 4.1.

5. Определить расчетным путем резонансную частоту _ри сравнить результат с экспериментом.

6. Построить в масштабе векторные диаграммы исследуемой цепи для трех различных режимов:

– X_L < X_C

– X_L = X_C

– X_L > X_C

Табл. 4.1

№ опыта	Эксперимент				Расчет
	f, Гц	U, B	I, A	P, Вт	R, Ом	XL,Ом	XC, Ом	Х, Ом	UL,B	UC, B	,º

Содержание отчета:

– схема исследуемой цепи (рис. 4.1)

– табл. 4.1

– расчет и графические построения согласно п.п. 3, 4, 5, 6 программы работы

– выводы

Варианты заданий

Табл. 4.2

№ варианта	Катушка индуктивности	Конденсатор
1	L1	С = 40 мкФ
2	L1	С = 50 мкФ
3	L1	С = 70 мкФ
4	L1	С = 90 мкФ
5	L1	С = 120 мкФ
6	L1	С = 150 мкФ

Контрольные вопросы

1. Объясните, при каких условиях и в какой цепи возникает резонанс напряжений? Каковы признаки возникновения резонанса напряжений?

2. В чем могут заключаться эксплуатационные опасности, связанные с явлением резонанса в реальных условиях и цепях?

3. Опишите энергетический процесс в цепи (рис. 4.1) при резонансе напряжений?

4. При каких условиях в цепи, содержащей катушку и конденсатор, мог бы иметь место незатухающий колебательный процесс?

Лабораторная работа № 5 Резонанс токов

Цель работы: исследование резонанса токов в электрической цепи, состоящей из параллельно включенных катушки индуктивности и конденсатора.

Общие сведения

Резонансом токов называется такой режим работы разветвленной электрической цепи, состоящей из включенных параллельно индуктивности и конденсатора, при котором реактивные проводимости ветвей b_Lиb_Cстановятся равными, что соответствует совпадению по фазе питающего напряжения и тока в неразветвленной части цепи.

Равенство реактивных проводимостей может быть получено в результате изменения емкости, индуктивности или частоты напряжения питания. В данной работе резонанс токов достигается путем изменения частоты питающего напряжения.

Рис.5.1

Действующие значения токов в ветвях, содержащих катушку индуктивности и конденсатор, в электрической схеме (рис 5.1) соответственно равны:

,

(5.1)

где – полная проводимость ветви с индуктивностью,

– активная проводимость ветви;

– индуктивная проводимость ветви.

,

(5.2)

где – полная проводимость ветви с индуктивностью,

– активная проводимость ветви;

– емкостная проводимость ветви.

Действующее значение тока в неразветвленной части схемы определяется соотношением:

,

(5.3)

где Y – полная проводимость схемы,

G=G_L+G_C– активная проводимость схемы,

B=B_L – B_C – реактивная проводимость схемы.

Согласно условию резонанса токов должно выполняться равенство:

BL=BC или.

(5.4)

Из последнего соотношения можно выразить резонансную частоту:

.

(5.5)

Величина угла сдвига фаз между питающим напряжением и током в неразветвленной части схемы рис.5.1 определяется выражением:

.

(5.6)

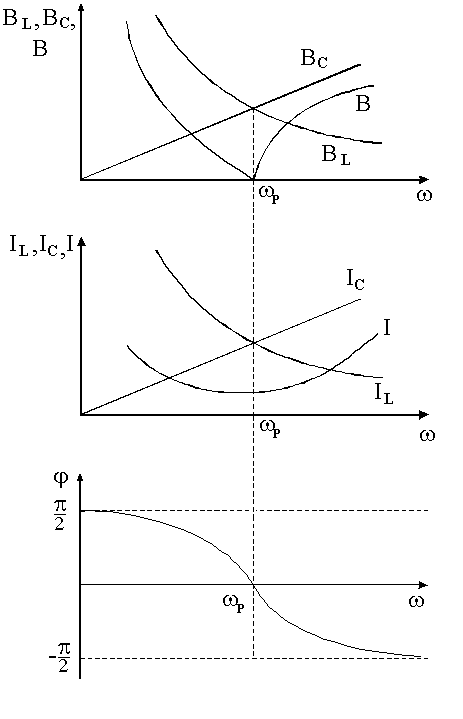
Примерный вид частотных характеристик схемы рис. 5.1 показан на рис. 5.2.

Рис.5.2