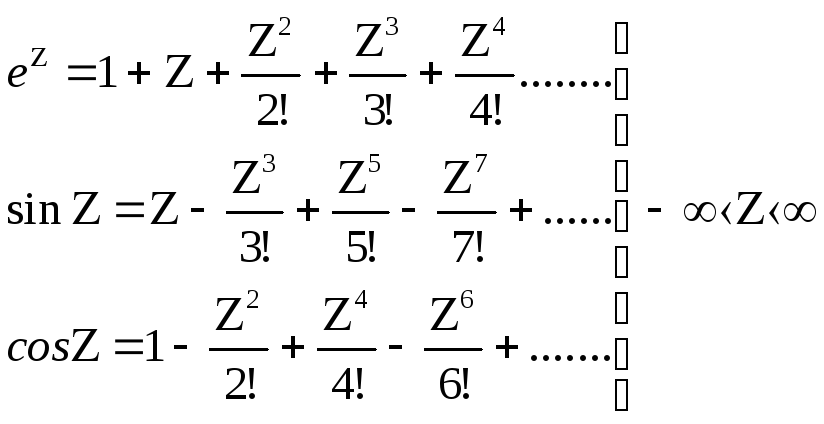
Основные разложения в ряд Маклорена.

Ниже приведены пять основных разложений и указаны интервалы сходимости:

ln (1+ Z) = Z - +....... –1 < Z < 1,

(1 + Z)^m = 1 + m Z + Z² + Z³ + Z⁴ + ...... , –1 < Z < 1.

Последний ряд называется БИНОМИАЛЬНЫМ (m может быть любым числом, в том числе дробным и отрицательным).

Вычисление значений функций с помощью рядов.

Пример. С точностью до 0,001 вычислить ln 1,2.

Решение. ln 1,2 = ln (1 + 0,2). Так как Z = 0,2 находится внутри промежутка –1 < Z < 1, то это значение можно подставить в разложении функции ln (1 + Z):

Ln(1 + 0,2) = 0,2 – 0,2²/2 + 0,2³/3 – 0,2⁴/4 +.......≈ 0,2 – 0,02 + 0,00267 – 0,0004 + .... ≈ 0,2 – 0,02 + 0,00267 ≈ 0,183

ln 1,2 ≈ 0,183.

ЭВМ вычисляют значения функций с помощью рядов.

Вычисление определенных интегралов с помощью рядов.

Ряд Тэйлора

Ряд Маклорена обычно используют для представления функции в окрестности точки х = 0. Для представления функции в окрестности точки х = х₀ ≠ 0, удобнее ряд Тэйлора : f (х) = f (х₀) + f'(х₀) (х – х₀) + (х – х₀)² + (х-х₀)³ + (х-х₀)⁴ + ....

2. ТЕОРИЯ ВЕРОЯТНОСТЕЙ.

2.1. Случайные события

Классическое определение вероятности.

Событие, которое в результате данного испытания может появиться, а может и не появится СЛУЧАЙНЫМ.

Например: испытание – подбрасывание монеты; случайное событие – выпадение герба.

События обозначают буквами А, В, С, ...

Количественной оценкой возможности появления события является его вероятность.

Вероятность события А обозначают Р (А) или р.

В ряде случаев вероятности события можно – подсчитать, используя классическое определение вероятности:

Р = m/п

Здесь п – общие число равновозможных исходов испытания;

13. число тех из них, которые благоприятствуют появлению события.

Пример. В ящике 5 шаров – 3 черных и 2 белых. Наугад вынимают один шар. Найти вероятность того, что он окажется черным.

Решение. Р = 3/5. («Равновозможность исходов испытания в данном случае означает, что шары неразличимы «на ощупь»).

Свойства вероятностей.

Событие называется достоверным, если в результате данного испытания оно обязательно проявляется.

Например, выпадение хотя бы одного очка при подбрасывании игральной кости (кубика).

Для достоверного события m = п р = 1

Вероятность достоверного события равна единицы

Если событие случайно, то 0 < m < n 0 < m < n < 1,

т.е. для случайного события 0 < р < 1.

Если появление некоторого события в данном испытании невозможно, то m = 0 р = 0.

Вероятность невозможного события равна нулю.

Устойчивость относительной частоты.

Повторим испытание много раз и запомним, сколько раз случайно событие появилась.

Отношение числа появлений события к числу испытаний называется его относительной частотой.

Например, при ста подбрасываниях монеты герб выпал 53 раза. Значит, относительная частота выпадений герба равна 53/100 = 0,53.

Наблюдения показывает, что относительная частота обладает свойством устойчивости:

При большом числе испытаний относительная частота события близка к его вероятности (и тем ближе, чем больше испытаний).

Так, в приведенном выше примере относительная частота выпадений герба 0,53 близка к вероятности этого события ½ = 0,5.

Свойство устойчивости позволяет предсказать, сколько примерно раз событие появится при заданном числе испытаний.

Пример. Сколько примерно раз выпадает единица при 1200 подбрасываниях игральной кости?

Решение.Вероятность выпадения единицы равна 1/6

≈