
- •Волжская государственная академия водного транспорта
- •Литература
- •2. Основные понятия и сведения
- •Дифференциальные уравнения первого порядка. Теорема существования и единственности решения дифференциального уравнения первого порядка.
- •Некоторые типы уравнений первого порядка.
- •Уравнения второго порядка.
- •Линейные уравнения с постоянными коэффициентами.
- •Возможны случаи:
- •Системы дифференцированных уравнений.
- •Задание на контрольную работу №5.
Волжская государственная академия водного транспорта
Кафедра математики
Б.С. Украинский
ОСНОВНЫЕ ПОНЯТИЯ ОБ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ
Методические указания к решению задач,
примеры и варианты контрольной работы № 4
для студентов - заочников всех специальностей
Н. Новгород
2000 г.
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Рабочий план-программа и методические указания
Обыкновенные дифференциальные уравнения и их решение.
Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Основные классы уравнений, интегрируемых в квадратурах.
Дифференциальные уравнения второго порядка. Задача Коши. Уравнения, допускающие понижение порядка.
Линейные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
Численное интегрирование дифференциальных уравнений.
Литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. – М.: Наука, 1970. – Т. 1;2, гл. XIII, №№ 1-11, 16-18; 20-25.
2. Задачи и упражнения по математическому анализу для втузов /Под ред. В.П. Демидовича. – М.: Наука, 1964.
Вопросы для самопроверки (вопросы экзаменационных билетов).
Определение дифференциального уравнения, его порядка и решения.
Определение уравнения первого порядка, формулировка и геометрический
смысл задачи Коши.
3. Формулировка теоремы существования и единственности решения задачи Коши для уравнения первого порядка.
4. Дифференциальные уравнения с разделяющимися переменными и метод нахождения их общих решений.
5. Однородные дифференциальные уравнения первого порядка и метод нахождения их общих решений.
6. Линейные дифференциальные уравнения первого порядка и метод нахождения их общих решений.
7.
Метод решения уравнений вида
![]() .
.
Метод решения уравнений вида
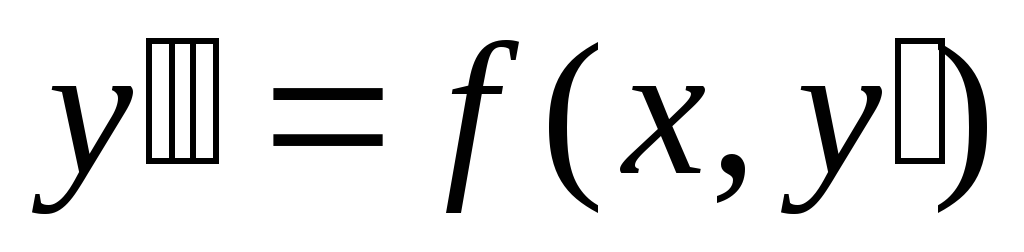 .
.Метод решения уравнений вида
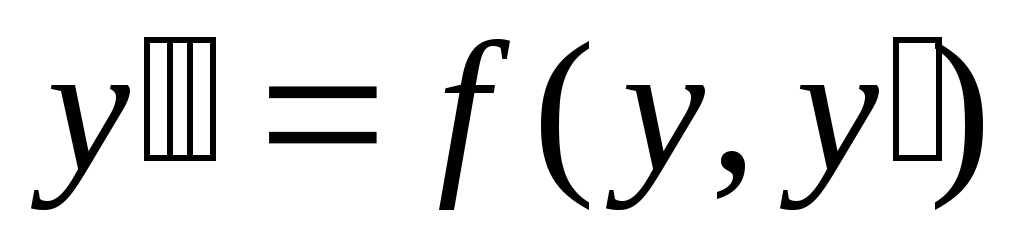 .
.Решение однородных линейных уравнений второго порядка с постоянными коэффициентами
Решение неоднородного уравнения второго порядка с постоянными коэффициентами и правой частью вида
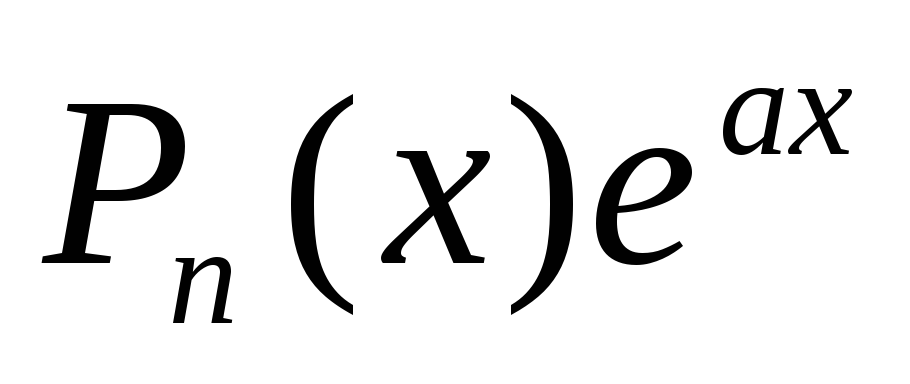 .
.Решение неординарного уравнения второго порядка с постоянными коэффициентами и правой частью вида
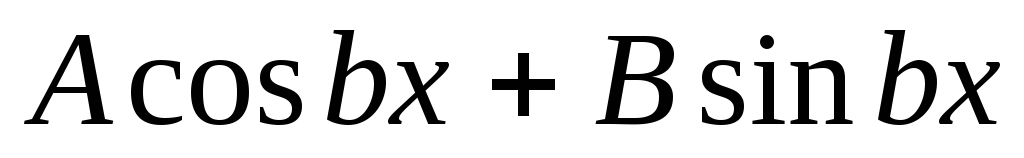
13. Метод Эйлера численного интегрирования дифференциальных уравнений.
2. Основные понятия и сведения
Определение
1. Обыкновенным дифференциальным
уравнением называется уравнение,
связывающее независимую переменную
![]() ,
искомую функцию
,
искомую функцию![]() и ее производные
и ее производные![]() ,
т.е. уравнение вида
,
т.е. уравнение вида
![]()
Определение 2. Порядком дифференциального уравнения называются порядок наивысшей производной, входящей в уравнение.
Пример. ![]() - уравнение третьего порядка.
- уравнение третьего порядка.
Определение
3. Решением или интегралом
дифференциального уравнения называется
всякая функция
![]() ,
обращающая его в тождество относительно
,
обращающая его в тождество относительно![]() .
.
Пример. ![]() - решение уравнения
- решение уравнения![]() так как
так как![]()
