
- •7. Дисперсия диэлектрической и магнитной проницаемости.
- •7.1. Причина появления дисперсии и область частот, в которой она имеет место и при этом применима макроскопическая теория.
- •7.3. Диэлектрическая проницаемость при очень высоких частотах.
- •7.4. Связь вещественной и мнимой частей диэлектрической и магнитной проницаемостей – уравнения Крамерса – Кронига. Свойства функции ε(ω).
- •7.4. Прозрачные среды.
7.4. Прозрачные среды.
Рассмотрим теперь поведение диэлектрической проницаемости ε(ω) в области (в диапазоне частот) прозрачности среды, т.е. где электромагнитные волны распространяются в среде с небольшим затуханием. В этом случае мнимая часть ε′′(ω) диэлектрической проницаемости отлична от нуля! но! очень мала, поэтому из-за последнего говорят, что в области прозрачности мнимой частью диэлектрической проницаемости можно пренебречь т.е. ε (ω) ≈ ε′(ω).
В таком случае в формуле (7.19) взятие главного значения интеграла становится бессмысленным, т.к. x = ω фактически выпадает из области интегрирования. После этого интеграл можно дифференцировать по параметру ω, как обычный интеграл, не имеющий особенностей в подынтегральном выражении. Тогда, произведя дифференцирование выражения (7.19) по частоте ω, получим
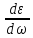 ≈
≈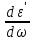 =
=
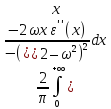 =
=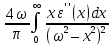 , т.е.
, т.е.
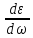 =
=
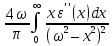 . (7.28)
. (7.28)
Подынтегральное
выражение в (7.28) во всей области
интегрирования больше нуля (напомним,
что ε′′(ω)
> 0 всегда),
следовательно, как само значение
интеграла, так и производная
 будут больше нуля
будут больше нуля
 >
0.
(7.21)
>
0.
(7.21)
Последнее означает, что в области отсутствия поглощения (прозрачности) диэлектрическая проницаемость – монотонно возрастающая функция частоты. Такое поведение функции ε(ω) – ее возрастание с увеличением частоты ω, принято называть нормальной дисперсией. Если наоборот ε(ω) уменьшается с ростом частоты, то – аномальной дисперсией.
Если правую и левую части выражения (7.19) умножить на ω2 , то аналогичным образом, в той же области частот (области прозрачности), после взятия производной получим другое неравенство,
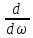 [ω2
(ε
– 1)]
=
[ω2
(ε
– 1)]
=
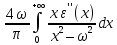 +ω2
+ω2
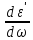 =,
используя для
=,
используя для
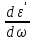 (7.28)
(7.28)
=
 =
=
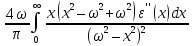 =
=
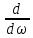 [ω2
(ε
– 1)]
=
[ω2
(ε
– 1)]
=
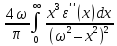 >
0,
>
0,
поскольку,
точно также в рассматриваемой области
значения подынтегрального выражения
всегда положительны. Вычислив производную
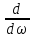 [ω2
(ε
– 1)]
= 2ω(ε
– 1)
+ ω2
[ω2
(ε
– 1)]
= 2ω(ε
– 1)
+ ω2
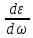 < 0,
получим следующее неравенство
< 0,
получим следующее неравенство
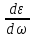 >
>
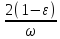 .
(7.22)
.
(7.22)
Это неравенство более сильное, чем неравенство (7.21) если диэлектрическая проницаемость ε < 1 или даже отрицательная (ε < 0).
Здесь
сразу можно отметить, что неравенства
(7.21) и (7.22) (и аналогичные для μ(ω))
автоматически гарантируют выполнение
неравенства u
< c
, т.е. групповая скорость u
(скорость распространения энергии или
волнового пакета) электромагнитной
волны в среде всегда меньше ее скорости
в вакууме c
(скорости
света в вакууме). Например, пусть среда
диэлектрик, тогда магнитную проницаемость
можно положить равной единице μ
= 1
и показатель преломления среды n
будет равен n
=
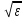 и
вводя n
вместо ε
в неравенства (7.21) и (7.22), получим:
и
вводя n
вместо ε
в неравенства (7.21) и (7.22), получим:
из
(7.21)
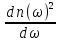 >
0 → 2n
>
0 → 2n
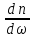 >
0 →
т.к. здесь ε
и,
соответственно n
>
1,
имеем
>
0 →
т.к. здесь ε
и,
соответственно n
>
1,
имеем
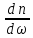 >
0 → т.к.
ω
>
0,
то ω
>
0 → т.к.
ω
>
0,
то ω
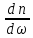 >
0 → ω
>
0 → ω
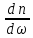 + n
>
n
→
+ n
>
n
→
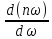 >
n,
>
n,
итак,
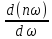 >
n;
(7.23)
>
n;
(7.23)
из
(7.22)
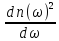 =
2n
=
2n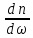 >
>
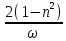 →
ω
→
ω
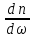 >
>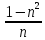 →ω
→ω
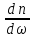 +n
>
+n
>
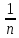 ,
и
,
и
окончательно
имеем
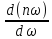 >
>
 .
(7.24)
.
(7.24)
Неравенство
(7.24) работает для ε
< 1
и, соответственно для n
<
1.
Тогда из выражения для групповой скорости
u
=
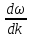 =
=
 , гдеk
– волновой вектор, модуль которого
равен k
=
, гдеk
– волновой вектор, модуль которого
равен k
=
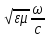 =n
=n
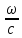 и неравенств (7.23) и (7.24) получаем,
соответственно, два неравенства: u
< c/n
(для n
>1)
и u
<
cn
(для n
< 1).
Из этих неравенств видно, что u
< c
как при n
>1,
так и при n
< 1.
Эти неравенства так же показывают, что
групповая скорость всегда больше нуля
u
>
0,
т.е. она направлена в туже сторону, что
и волновой вектор.
и неравенств (7.23) и (7.24) получаем,
соответственно, два неравенства: u
< c/n
(для n
>1)
и u
<
cn
(для n
< 1).
Из этих неравенств видно, что u
< c
как при n
>1,
так и при n
< 1.
Эти неравенства так же показывают, что
групповая скорость всегда больше нуля
u
>
0,
т.е. она направлена в туже сторону, что
и волновой вектор.
Вернемся к рассмотрению поведения ε в области прозрачности. Пусть область слабого поглощения простирается в некотором широком диапазоне частот от ω1 до ω2 , т.е. ω2 >> ω1 и рассмотрим частоты ω (при которых определяем ε (ω)), лежащие в этом диапазоне, так что ω1 << ω << ω2. Тогда область интегрирования в (7.19) разбивается на две части: x < ω1 и x > ω2. В первой из них можно пренебречь в знаменателе подынтегрального выражения x по сравнению с ω, а во второй, наоборот, – ω по сравнению с x и тогда:
ε
(ω)
≈ ε′(
ω) = 1+
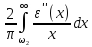 –
–
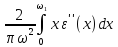 .
(7.25)
.
(7.25)
Область интегрирования от ω1 до ω2 отсутствует, т.к. в ней полагаем ε′′(ω) ≈ 0 и, соответственно, считаем, что интеграл по этому диапазону примерно равен нулю (точнее он, просто, значительно меньше всех трех слагаемых в правой части выражения (7.25) – единицы и двух интегралов). Оба интеграла в (7.25) имеют положительные значения, как и все значения в подынтегральных выражениях, поэтому функция ε(ω) в рассматриваемой области имеет вид a – b/ω2, где a и b положительные постоянные. Вторую из них можно выразить через силу осцилляторов N1
N1
=
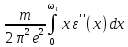 ,
ответственных за поглощение в области
от0
до
ω1
(в соответствии с (7.23) и (7.24)) и тогда
,
ответственных за поглощение в области
от0
до
ω1
(в соответствии с (7.23) и (7.24)) и тогда
ε
(ω)
= a
–
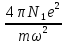 .
(7.26)
.
(7.26)
Из последнего выражения следует, что в достаточно широко области слабого поглощения диэлектрическая проницаемость, вообще говоря, может проходить через ноль. Однако в этой связи необходимо отметить (напомнить), что прозрачной в буквальном смысле слова является среда, в которой ε(ω) не только вещественно, но и положительно, т.к. при отрицательном ε волна затухает в глубь среды, хотя в ней и не происходит истинной диссипации энергии (энергия электромагнитного поля не переходит в другие виды энергий, например в тепло).
Для частоты, при которой ε = 0 , индукция D тождественно обращается в нуль и уравнения Максвелла допускают существование переменного электрического поля, удовлетворяющего одному лишь уравнению rot E = 0 при равном нулю магнитном поле. То есть, в этом случае возможно существование продольных электрических волн.
Вернемся
к обсуждению дисперсии. Пусть, наконец,
в широкой области прозрачности имеется
узкая область поглощения (ее называют
– «линия» поглощения) вокруг
некоторой частоты ω0.
«Линия»
поглощения – полоса частот Δω
(в
рассматриваемом случае она равна γ),
центральная частота которой ω0,
соответствует одному из возможных
переходов, например атома, из одного
энергетического состояния 𝓔1
в другое 𝓔2
(𝓔2
> 𝓔1),
при этом ω0
=
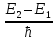 .
Рассмотрим окрестность этой частоты,
удовлетворяющую условию
.
Рассмотрим окрестность этой частоты,
удовлетворяющую условию
γ << |ω – ω0| << ω0, (7.27)
где γ – ширина линии. В этой области (в полосе частот γ) в подынтегральном выражении в (7.17) можно заменить x на ω0 везде, кроме быстроменяющейся функции ε′′(ω). Тогда получим:
ε
(ω)
≈ ε′(
ω) ≈
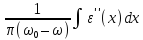 ,
(7.28)
,
(7.28)
где
интегрирование производится по линии
поглощения. В
этой области выражение
(7.28) определяет фактически только добавку
к итоговому значению ε(ω),
вычисляемой
по формуле (7.25).
Главного значения интеграла мы не пишем,
т.к. нашими действиями мы исключили
особую точку ω
= ω0
в области интегрирования γ.
Однако из выражения (7.28) мы, на первый
взгляд, видим, что при ω
= ω0
добавка к ε
(ω)
у нас обращается в бесконечность. Эта
особенность разрешается, если учесть
условие (7.27) (линия поглощения имеет
конечную ширину γ,
а не бесконечно узкую, поэтому и ε′′(ω0)
тоже имеет конечное значение). Поэтому
при расчете ε
(ω),
когда ω
лежит в полосе частот γ,
в формуле (7.28) разность частот
ω0
– ω (в
знаменателе) заменяется на γ/2, если ω
< ω0
и на – γ/2,
если ω
> ω0.
Поэтому добавка к ε(ω),
(точнее
ее модуль)
также имеет конечный максимум в полосе
γ.
Причем их два – слева от ω0
(ω
< ω0),
он положительный и справа (ω
> ω0),
– отрицательный, а в центре при ω
= ω0
добавка равна нулю. Эта картина поведения
ε′′(ω)
и
добавки к ε(ω),
рассчитываемой по формуле (7.28)
от частоты в полосе частот γ
приведена на рис.7.1. Из рисунка видно,
что Рис.7.1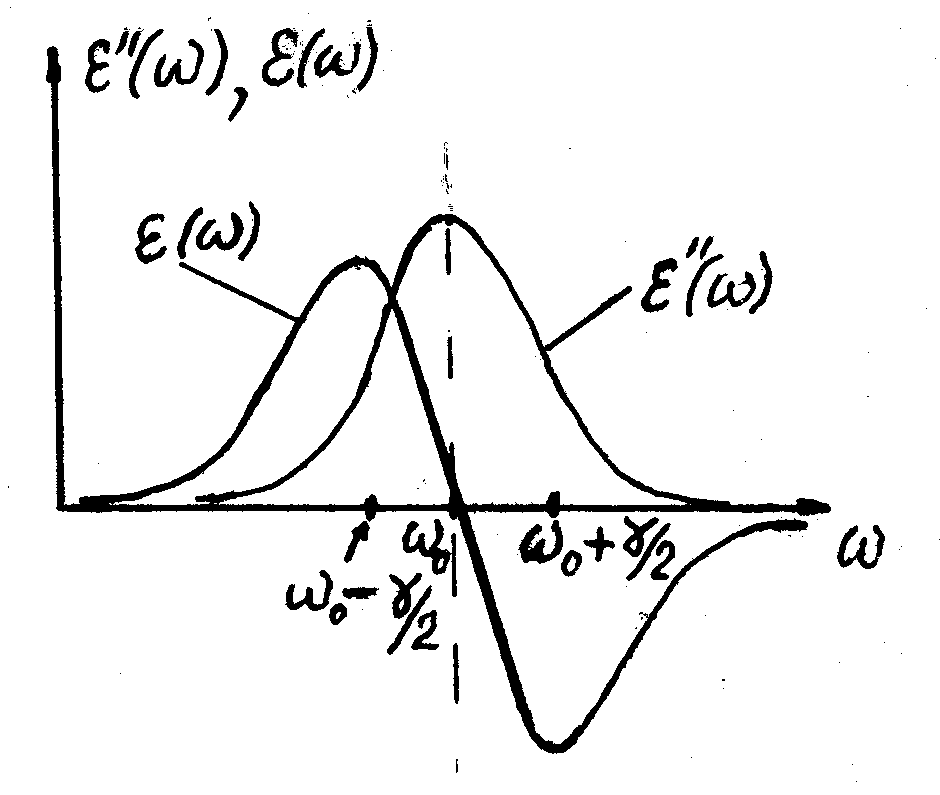
в середине области линии поглощения в интервале частот ω от ω0 – γ/2 до ω0 + γ/2 мы имеем аномальную дисперсию, а за его пределами, и слева, и справа – нормальную дисперсию. Но при этом отметим, что ширина γ этих линий очень узкая γ << ω0. Таких линий в области прозрачности может быть много. Они отличаются друг от друга интенсивностью линии поглощения (максимальным значением ε′′(ω0i)) и их шириной γi.
Таким
образом, из всего приведенного выше
анализа аналитических свойств функции
ε(ω)
= ε′(ω)
+ i
ε′′(ω)
можно привести следующую картину
возможного поведения вещественной и
мнимой частей диэлектрической
проницаемости, например диэлектрика,
при изменении частоты от 0 и до
бесконечности, точнее до очень высоких
частот ω
(до
ω
<< 2πс/a,
напомним – это условие применимости
макроскопических уравнений Максвелла).
Эта картина приведена на рис.7.2. Из нее
видно, что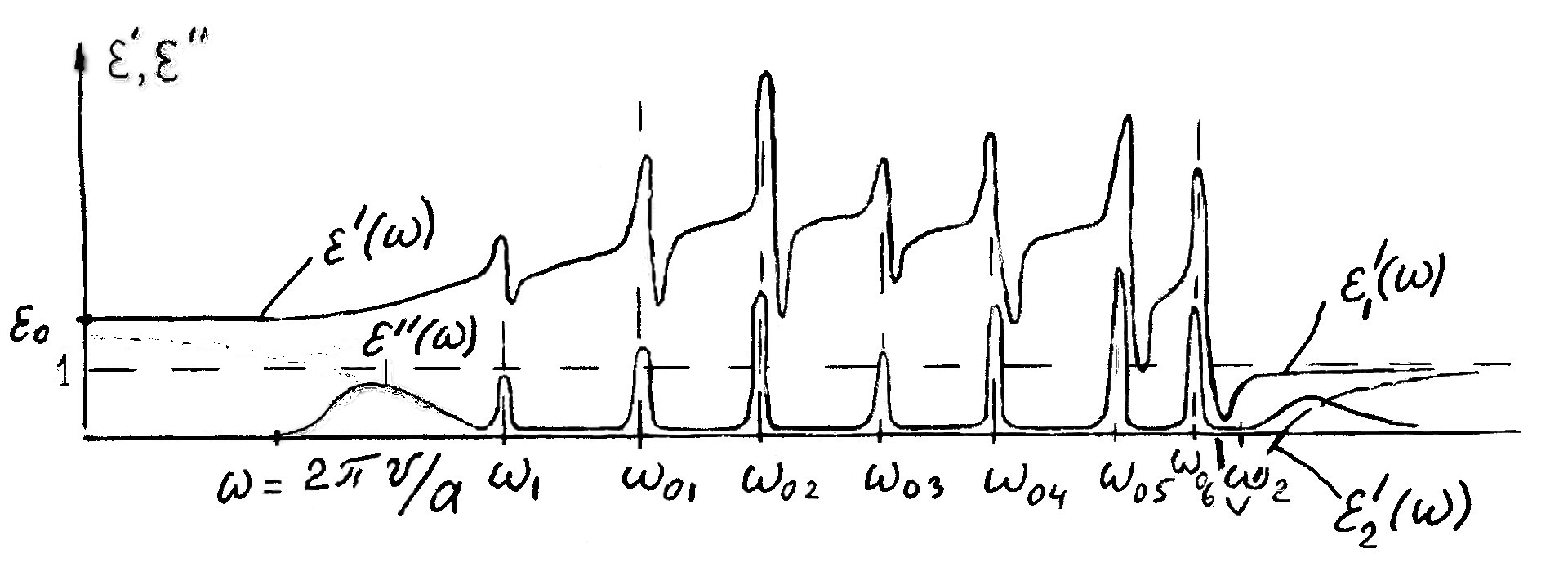
Рис.7.2
при
частотах 0
≤
ω
< 2πυ/a
(это
грубо точнее << 2πυ/a)
релаксационные процессы успевают
отслеживать изменение поляризации Р
диэлектрика (намагниченности …) за
изменением напряженности поля Е
и,
соответственно, здесь вещественная
часть диэлектрической
проницаемости
ε′(ω)
остается
постоянной и равной ε0
–диэлектрической проницаемости в
случае статического плоя, а ее мнимая
часть ε′′(ω)
=
0
(т.е. здесь ε(ω)
= ε0).
При частотах больших ω
> 2πυ/a
(опять грубо) релаксационные процессы
перестают успевать отслеживать изменение
поляризации Р
за изменением Е
(можно сказать, что Р
начинает
отставать по фазе за изменением Е
т.е. если закон изменения последнего
записать как Е
= Е0cos(ωt),
то для Р
будет Р
= Р0cos(ωt
– δ1),
соответственно и D
= Е
+
4πР
= D0cos(ωt
– δ),
т.е.
тоже отстает по фазе от Е).
В результате появляются потери на
переполяризацию (перемагничивание…)
диэлектрика (как в петле гистерезиса,
только в области малых полей, где имеется
линейность) и, соответственно, мнимая
часть ε′′(ω)
становится отличной от нуля. С ростом
частоты запаздывание δ1
для Р
и δ
для
D
увеличивается и увеличивается ε′′(ω),
а с ней и ε′(ω)
в
соответствии с уравнением (7.19).
При подходе к области прозрачности
ε′′(ω)
быстро падет и становится примерно
равной нулю (но все же больше нуля). Далее
мы попадаем в область прозрачности
(интервал частот от ω1
до ω2),
если она есть, в которой имеется несколько
линий поглощения разной интенсивности.
В пределах всей области прозрачности
между линиями поглощения ε′(ω)
растет, а в пределах каждой линии
поглощения делает зигзаг, как на рис.7.1,
и в близи центра каждой линии мы имеем
аномальную дисперсию. При этом после
прохождения каждой линии величина ε′(ω)
оказывается меньше чем она была
непосредственно перед подходом к линии
поглощения ( т.е. имеем отрицательный
перепад в значении ε′(ω)).
Этот перепад связан с тем, что линия
поглощения, как уже отмечалось ранее,
это соответствующий переход атома из
одного энергетического состояния в
другое и ему присущ определенный
электрон, который и называют дисперсным.
Когда ω
<
ω0
этот
дисперсный электрон дает вклад в
нормальную дисперсию (в слагаемое а
выражения
(7.25)),
а после прохождения лини ω
>
ω0,
наоборот, начинает давать вклад в
отрицательную дисперсию (в слагаемое
b
выражения
(7.25)).
Эта картина соответствует поведению
фазы вынужденных колебании в колебательном
контуре – отставание и опережение фаза
при ω
<
ω0
и ω
>
ω0,
соответственно. Размах зигзага и величина
перепада пропорциональны интенсивности
(максимуму ε′′(ω0
в центре линии)).
При таком изменении, где то (на рисунке
в самом конце области прозрачности)
после очередного сильного зигзага ε′(ω)
может оказаться меньше единицы (на
рисунке показано поведением ε′1(ω))
или даже меньше нуля (поведение
ε′2(ω)).
И далее если впереди (при более высоких
частотах) линий поглощения нет, значение
ε′(ω)
растет, приближаясь к единице снизу по
закону (7.26)
ε(ω)
= ε′(ω)
=
1 –
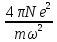 .
Здесь ε′′(ω)
становится
примерно равной нулю, поэтому поставлено
ε(ω)
= ε′(ω).
.
Здесь ε′′(ω)
становится
примерно равной нулю, поэтому поставлено
ε(ω)
= ε′(ω).
Плоская электромагнитная волна
Для монохроматических полей, меняющихся по закону ~ е–iωt уравнения Максвелла (7.4), в отсутствии сторонних зарядов и токов проводимости имеют вид:
c rot H = – iω ε(ω) E, c rot E = iω μ(ω) H (7.29)
Эти
уравнения уже сами по себе составляют
полную систему, т.к. уравнения (7.3) (div
D
= 0 и div
B
= 0)
следуют из них автоматически. (Для
доказательства нужно взять дивергенцию
от этих уравнений и тогда, например, div
от
первого уравнения дает –
iωdivε(ω)E
= cdiv(rotH)
и т.к. div(rot
H)
=
0,
 H])
=
0 (результат
векторного произведения
H])
=
0 (результат
векторного произведения
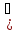 H]
перпендикулярен
H]
перпендикулярен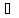 и,
соответственно, их скалярное произведение
равно нулю),
получаем, учитывая, что ε(ω)E
= D,
div
D
= 0).
Таким образом,
уравнения
(7.29)
не должны рассматриваться отдельно.
Если теперь положить среду однородной,
то по аналогии с выводом уравнений (1.8)
(берем rot
от
уравнений, используем соотношение из
векторной алгебры rot(rot
a)
≡
и,
соответственно, их скалярное произведение
равно нулю),
получаем, учитывая, что ε(ω)E
= D,
div
D
= 0).
Таким образом,
уравнения
(7.29)
не должны рассматриваться отдельно.
Если теперь положить среду однородной,
то по аналогии с выводом уравнений (1.8)
(берем rot
от
уравнений, используем соотношение из
векторной алгебры rot(rot
a)
≡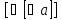 = ≡(
= ≡( 2a
= grad(div
a)
–
2a
= grad(div
a)
–
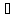 2a
,
исключаем в этих уравнениях Е
или Н,
используя (7.29)
и используем условие отсутствия токов
проводимости и сторонних зарядов)
получим
следующие уравнения (второго порядка)
для монохроматических полей H
и Е:
2a
,
исключаем в этих уравнениях Е
или Н,
используя (7.29)
и используем условие отсутствия токов
проводимости и сторонних зарядов)
получим
следующие уравнения (второго порядка)
для монохроматических полей H
и Е:
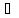 2H
+
εμ
2H
+
εμ
 Н
=
0
или, тождественно, т.к.
Н
=
0
или, тождественно, т.к.
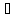 2
≡
Δ
2
≡
Δ
ΔH
+
εμ
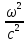 Н
=
0,
ΔЕ
+
εμ
Н
=
0,
ΔЕ
+
εμ
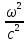 Е
=
0
.
(7.30)
Е
=
0
.
(7.30)
(Фактически
для получения (7.30)
в волновых уравнениях (1.8) – лекция 1, мы
взяли (раскрыли) вторую производную по
времени
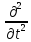 = –ω2.)
= –ω2.)
Рассмотрим плоскую электромагнитную волну, распространяющуюся в неограниченной однородной среде. В плоской волне в вакууме зависимость поля от координаты дается волновым множителем вида еikr с вещественным волновым вектором k (k = ω/с =2π/λ, где λ – длина волны в вакууме). И поле, например Е (для Н аналогично), в плоской электромагнитной волне имеет вид
Е= Е0 е–i (ωt–kr) , (7.31)
где Е0 – амплитуда (вектор, направление которого определяет поляризацию волны), а (ωt–kr) – фаза. Напомним, плоская волна – волна имеющая плоский фазовый фронт (фазовый фронт – геометрическое место точек в пространстве, в котором фаза волны постоянная, в (7.31) это плоскость перпендикулярная волновому вектору k) и значение Е постоянно на поверхности фазового фронта. При рассмотрении же распространения волн в материальных средах в общем случае (из-за наличия дисперсии – ε(ω) и μ(ω) комплексные значения) оказывается необходимым вводить так же и комплексные значения волновых векторов волн:
k = k′ + ik′′ ,
где k′ и k′′ – вещественные векторы.
Положив Е и Н в виде (7.31), после подстановки их в уравнения (7.29) и произведя дифференцирование по координатам, получим
ωμ Н = с[kЕ], ωε Е = – с[kН]. (7.32)
(rot
Е
= [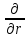 Е]
= i[kЕ]
(Е
~
еi
kr),
второе аналогично) Выражения (7.32) в общем
случае дают связь между компонентами
электрического и магнитного полей.
Исключив из этих двух соотношений (7.32)
Е
и Н,
найдем следующее выражение для квадрата
волнового вектора: (например из первого
Н
=
с[kЕ]
/ ωμ,
подставляем
во второе → εμ
Е]
= i[kЕ]
(Е
~
еi
kr),
второе аналогично) Выражения (7.32) в общем
случае дают связь между компонентами
электрического и магнитного полей.
Исключив из этих двух соотношений (7.32)
Е
и Н,
найдем следующее выражение для квадрата
волнового вектора: (например из первого
Н
=
с[kЕ]
/ ωμ,
подставляем
во второе → εμ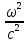 Е
=
–
[k[kЕ]]
= (используя
[а[вс]]
=
в(ас)
– с(ав))
= – k(kЕ)
+ Е(k2)
= Е(k2)
(т.к.
k
перпендикулярен
Е,
то скалярное произведение (kЕ)
= 0) и
после сокращения Е
окончательно
имеем)
Е
=
–
[k[kЕ]]
= (используя
[а[вс]]
=
в(ас)
– с(ав))
= – k(kЕ)
+ Е(k2)
= Е(k2)
(т.к.
k
перпендикулярен
Е,
то скалярное произведение (kЕ)
= 0) и
после сокращения Е
окончательно
имеем)
k2
≡
k′
2
–
k′′
2
+ 2
k′
k′′
= εμ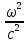 .
(7.33)
.
(7.33)
Из (7.33) видно, что вектор k может быть вещественным, только если ε и μ вещественны и положительны. Но даже в этом случае k может быть комплексным, если скалярное произведение векторов k′ k′′ = 0 (это соответствует, например, случаю полного внутреннего отражения волны на границе двух диэлектриков).
Теперь следует иметь в виду, что в общем случае комплексных волна может быть названа «плоской» лишь в условном смысле. Если записать, что
еi kr = еi(k′ + ik′′)r = еi k′r е –ik′′r,
то видно, что плоскости перпендикулярные к вектору k′, являются плоскостями постоянной фазы, а плоскости перпендикулярные вектору k′′, в направлении которого происходит затухание волны, являются плоскостями постоянной амплитуды. Что же касается поверхностей постоянного значения самого поля, то они в общем случае вообще не будут плоскими. Такие волны называют неоднородными плоскими волнами, в отличие от обычных однородных плоских волн.
Умножив формулы (7.32) скалярно на волновой вектор k, получим
kЕ = 0 kН = 0. (7.34)
Из (7.34) следует, что Е и Н перпендикулярны k. Если же возвести любую из формул (7.32) в квадрат и использовать (7.33), то будем иметь
Е2
=
 Н2 (7.35)
Н2 (7.35)
Следует, однако, иметь в виду, что все три вектора k, Е и Н в соотношениях (7.34) и (7.35) комплексные, поэтому эти соотношения не имеют того наглядного смысла, который они имели бы в случае вещественных величин.
Пусть волна распространяется без затухания в однородной непоглощающей (прозрачной) среде. В этом случае волновой вектор вещественен и по величине равен
k
=
 = n
= n
 , (7.36)
, (7.36)
где
n
=
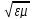 называется показателем преломления
среды. Как электрическое, так и магнитное
поля лежат в плоскости перпендикулярной
к волновому вектору k
(т.е. имеем чисто поперечную волну), при
этом перпендикулярны друг к другу и
связаны соотношением
называется показателем преломления
среды. Как электрическое, так и магнитное
поля лежат в плоскости перпендикулярной
к волновому вектору k
(т.е. имеем чисто поперечную волну), при
этом перпендикулярны друг к другу и
связаны соотношением
Н
=
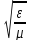 [lE], (7.37)
[lE], (7.37)
где l – единичный вектор в направлении k. Из (7.37) следует, что
εЕЕ* = μНН*
это,
однако не означает равенства электрической
и магнитной энергий (как в отсутствии
дисперсии), поскольку последние даются
другими выражениями (в отличие от
известных вам в диэлектрической среде
в отсутствии дисперсии, когда ε
и μ
являются вещественными постоянными: S
=
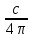 [EH]
–
плотность потока энергии (вектор Умова
– Пойнтинга); изменение (в 1 секунду)
энергии, сосредоточенной в единице
объема тела, вычисляемой как div
S
=
–
[EH]
–
плотность потока энергии (вектор Умова
– Пойнтинга); изменение (в 1 секунду)
энергии, сосредоточенной в единице
объема тела, вычисляемой как div
S
=
–
 (Е
(Е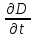 +
Н
+
Н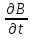 )
=
)
=
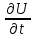 ,
где
изменение
электромагнитной энергии U
=
,
где
изменение
электромагнитной энергии U
=
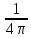 (εЕ2
+
μН2)).
Суммарную плотность электромагнитной
энергии в этом случае можно привести к
виду
(εЕ2
+
μН2)).
Суммарную плотность электромагнитной
энергии в этом случае можно привести к
виду
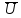 =
=
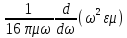 EE*
=
EE*
=
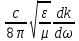 EE*. (7.38)
EE*. (7.38)
Скорость u распространения энергии (волнового пакета, групповая скорость) волны в среде определяется известным выражением:
u
=
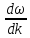 =
=
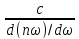 . (7.39)
. (7.39)
При
этом u
=
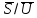 ,
в соответствии с ее смыслом как скорости
переноса энергии в волновом пакете,
здесь
,
в соответствии с ее смыслом как скорости
переноса энергии в волновом пакете,
здесь
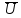 – плотность энергии , даваемая формулой(7.38),
а
– плотность энергии , даваемая формулой(7.38),
а
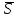 =
=
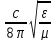 EE* (7.40)
EE* (7.40)
–
среднее
значение вектора Умова
– Пойнтинга. В отсутствии дисперсии,
когда показатель преломления не зависит
от частоты, выражение (7.39)
сводится просто к u
=
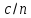 .
.
Теперь рассмотрим более общий случай распространения электромагнитной волны в поглощающей среде, причем волновой вектор имеет определенное направление, т.е. k′ и k′′ параллельны друг другу. Такая волна является плоской в буквальном смысле, т.к. поверхностями постоянных значений поля в ней являются плоскости, перпендикулярные к направлению распространения (они же – плоскости равных фаз – фронты), т.е. имеем однородную плоскую волу.
В этом случае можно ввести комплексную «длину» k волнового вектора, как k = k l, где l – единичный вектор в направлении k′ и k′′ и из (7.33) имеем
k
=
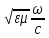 = (n
+ iæ)
= (n
+ iæ) . (7.41)
. (7.41)
величину n называют показателем преломления, а æ – коэффициентом поглощения среды; последний определяет скорость затухания волны по мере ее распространения. Здесь необходимо заметить, что затухание волны не обязательно связано с наличием истинного поглощения; диссипация энергии имеет место лишь при комплексных ε или μ, а коэффициент æ может быть отличным от нуля и при вещественных (отрицательных) ε и μ.
Выразим величины n и æ через вещественную и мнимую части диэлектрической проницаемости, предполагая при этом, что μ = 1. Из равенства n2 – æ2 + 2inæ = ε = ε′ + i ε′′ имеем
n2 – æ2 = ε′, 2næ = ε′′.
Решая эти уравнения относительно n и æ, получим
n
=
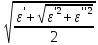 ,
æ
=
,
æ
=
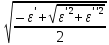 .
(7.42)
.
(7.42)
В
частности, для металлов в области частот,
где справедливо выражение
ε(ω)
= i
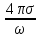 (7.15)
(это при малых частотах ω → 0) мнимая
часть ε
велика по сравнению с вещественной
частью и связана с проводимостью
посредством ε′′
=
(7.15)
(это при малых частотах ω → 0) мнимая
часть ε
велика по сравнению с вещественной
частью и связана с проводимостью
посредством ε′′
=
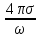 ;
тогда, пренебрегая ε′
по сравнению с ε′′,
найдем, что n
и
æ
совпадают и равны
;
тогда, пренебрегая ε′
по сравнению с ε′′,
найдем, что n
и
æ
совпадают и равны
n
=
æ
=
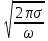 .
(7.43)
.
(7.43)
Для
связи между Е
и
Н
в рассматриваемой однородной плоской
волне снов получаем выражение (7.37) Н
=
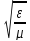 [lE],
но только с комплексными ε
и
μ.
Оно снова показывает, что поля Е
и
Н
перпендикулярны к направлению
распространения волны и друг к другу.
Если
μ
= 1
, то, написав
[lE],
но только с комплексными ε
и
μ.
Оно снова показывает, что поля Е
и
Н
перпендикулярны к направлению
распространения волны и друг к другу.
Если
μ
= 1
, то, написав
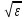 в виде
в виде
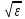 =
=
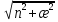 exp[i
arctg(æ/n)],
exp[i
arctg(æ/n)],
видно,
что магнитное поле по абсолютной величине
превышает электрическое в
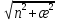 раз,
а по фазе отстает от него на угол
arctg(æ/n);
в случае (7.43)
(для металлов) сдвиг фаз равен π/4.
раз,
а по фазе отстает от него на угол
arctg(æ/n);
в случае (7.43)
(для металлов) сдвиг фаз равен π/4.
