
- •7. Дисперсия диэлектрической и магнитной проницаемости.
- •7.1. Причина появления дисперсии и область частот, в которой она имеет место и при этом применима макроскопическая теория.
- •7.3. Диэлектрическая проницаемость при очень высоких частотах.
- •7.4. Связь вещественной и мнимой частей диэлектрической и магнитной проницаемостей – уравнения Крамерса – Кронига. Свойства функции ε(ω).
- •7.4. Прозрачные среды.
7.3. Диэлектрическая проницаемость при очень высоких частотах.
Из
простых физических соображений можно
сразу предположить, что при ω
→
 функция
ε(ω)
должна стремиться к единице, т.к. при
очень быстропеременном поле процесса
поляризации, приводящего к отличию
индукции D
от напряженности E
электрического поля не должны происходить.
Установим эту зависимость.
функция
ε(ω)
должна стремиться к единице, т.к. при
очень быстропеременном поле процесса
поляризации, приводящего к отличию
индукции D
от напряженности E
электрического поля не должны происходить.
Установим эту зависимость.
В соответствии с только что сказанным, мы должны положить частоту ω значительно большей частот движения всех электронов в атомах (или, по крайней мере, их большинства) данного вещества (частота движения – величина обратная соответствующему времени релаксации). При этом условии при вычислении поляризации вещества можно рассматривать электроны как свободные, пренебрегая их взаимодействием друг с другом и с ядрами атомов. (Напомним – у нас еще выполнено условие (7.2) λ >> a или эквивалентное ω/2π = ν << с/a , необходимое для использования макроскопической теории.)
При
указанных условиях, расстояния υ
 , проходимые электронами в течение
периода волны, малы по сравнению, как с
длиной волны λ,
так и с размером a
атома. Кроме этого при определении
скорости и смещения, приобретаемым
электроном в поле электромагнитной
волны, последнее (поле) можно считать
однородным.
, проходимые электронами в течение
периода волны, малы по сравнению, как с
длиной волны λ,
так и с размером a
атома. Кроме этого при определении
скорости и смещения, приобретаемым
электроном в поле электромагнитной
волны, последнее (поле) можно считать
однородным.
Уравнение
движения электрона в переменном (во
времени) поле имеет вид m
 =
eE
=
eE0e–iωt
, где m,
e
– масса и заряд электрона, а E0
–амплитуда переменного поля. Представим
скорость υ
движения электрона в виде υ
=
υ0
+
=
eE
=
eE0e–iωt
, где m,
e
– масса и заряд электрона, а E0
–амплитуда переменного поля. Представим
скорость υ
движения электрона в виде υ
=
υ0
+
 и, соответствующее им смещение r
=
r0
+
и, соответствующее им смещение r
=
r0
+
 , и учтем, что для реальных полей υ0
>>
, и учтем, что для реальных полей υ0
>>
 r0
>>
r0
>>
 . Тогда уравнение движения примет вид
m
. Тогда уравнение движения примет вид
m
 =
eE0
e–iωt
. Дважды проинтегрировав это уравнение,
получим (
=
eE0
e–iωt
. Дважды проинтегрировав это уравнение,
получим (
 =
=
 )
)
 =
– eE/mω2
. Полученное выражение относится к
любому электрону в атомах вещества.
Поляризация вещества Р
есть дипольный момент единицы его объема
(Р
= n<р>).
Суммируя по всем электронам, находим Р
=
– eE/mω2
. Полученное выражение относится к
любому электрону в атомах вещества.
Поляризация вещества Р
есть дипольный момент единицы его объема
(Р
= n<р>).
Суммируя по всем электронам, находим Р
Р
=
 = –
= –
 NE
,
NE
,
Где N – число электронов во всех атомах единицы объема вещества. По определению электрической индукции D = εE = Е +4πР. Отсюда получаем следующее выражение для ε:
ε(ω)
= 1 –
 . (7.16)
. (7.16)
Фактическая область применения этой формулы начинается от дальнего ультрафиолета у самых легких элементов или от рентгеновских частот у более тяжелых элементов. И заметим, что данная формула работает и для частот (длин волн) выше границы применимости макроскопической теории, т.е. может ω/2π >> с/a или λ << a .
Итак, из выражения (7.16) видно, что для очень больших частот ε(ω) растет с увеличением частоты, приближаясь к единице снизу.
7.4. Связь вещественной и мнимой частей диэлектрической и магнитной проницаемостей – уравнения Крамерса – Кронига. Свойства функции ε(ω).
Ранее
мы установили связь между D
и
E,
которая для монохроматических полей
имеет
вид D
=
ε(ω)E
(7.9),
где функция ε(ω)
определяется
как ε(ω)
= 1 +
 (7.10).
При этом ε(ω)
комплексная ε(ω)
= ε′(ω)
+ i
ε′′(ω)
(7.11)
и ε′(ω)
– четная,
а ε′′(ω)
– нечетная функции.
Кроме того, сразу отметим еще одно
свойство последней, – она всегда
положительная ε′′(ω)
> 0
(μ′′(ω)
> 0).
Эта составляющая, как будет показано
ниже, определяет потери (диссипацию)
переменного электромагнитного поля на
переполяризацию и перемагничевание
вещества, идущие на нагрев последнего
(как при гистерезисе) и согласно второму
закону термодинамики – энтропия растет
и, соответственно, ε′′(ω)
> 0
.
(7.10).
При этом ε(ω)
комплексная ε(ω)
= ε′(ω)
+ i
ε′′(ω)
(7.11)
и ε′(ω)
– четная,
а ε′′(ω)
– нечетная функции.
Кроме того, сразу отметим еще одно
свойство последней, – она всегда
положительная ε′′(ω)
> 0
(μ′′(ω)
> 0).
Эта составляющая, как будет показано
ниже, определяет потери (диссипацию)
переменного электромагнитного поля на
переполяризацию и перемагничевание
вещества, идущие на нагрев последнего
(как при гистерезисе) и согласно второму
закону термодинамики – энтропия растет
и, соответственно, ε′′(ω)
> 0
.
Между вещественной и мнимой частями диэлектрической (и магнитной) проницаемости имеется определенная связь, установленная Крамерсом и Кронигом (H.A.Kramers, R.L. Kronig) в 1927 г, которая имеет вид:
ε′(ω)
– 1 =
 (7.17)
(7.17)
ε′′(ω)
= –
 ,
(7.18)
,
(7.18)
где перечеркнутый знак интеграла означает, что интеграл от полюсного выражения понимается в смысле его главного значения:
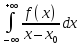 =
=
 +
+

Так как ε′′(ω) нечетная функция, то (7.17) можно переписать еще и так
ε′(ω)
– 1 =
 =
=
 +
+
 =,
произведя в первом интеграле замену
переменной x
на –x
и учтя, что ε′′(–x)
= – ε′′(x)
получим
=,
произведя в первом интеграле замену
переменной x
на –x
и учтя, что ε′′(–x)
= – ε′′(x)
получим



=
 +
+
 =
= =
=


=
 =
= ,и
окончательно имеем:
,и
окончательно имеем:

ε′(ω)
– 1 =
 . (7.19)
. (7.19)
Для
проводников
в точке ω
= 0,
как
мы ранее отметили, функция ε(ω)
имеет полюс (особенность при ω
→ 0),
вблизи которой ε(ω)
=
 (7.15).
Эта мнимая добавка, соответственно,
присутствует и в выражении (7.18) для
мнимой составляющей диэлектрической
проницаемости ε′′(ω)
и для проводников оно имеет вид:
(7.15).
Эта мнимая добавка, соответственно,
присутствует и в выражении (7.18) для
мнимой составляющей диэлектрической
проницаемости ε′′(ω)
и для проводников оно имеет вид:
ε′′(ω)
= –
 +
+
 .
(7.20)
.
(7.20)
Формулы (7.17) и (7.19) для вещественной части диэлектрической проницаемости ε′(ω) остаются прежними.
Из приведенных выражений для ε′(ω) и ε′′(ω) особенно существенна формула (7.17) (или (7.19)). С ее помощью можно вычислить ε′(ω), если для данного тела известна хотя бы приближенная формула для ε′′(ω), полученная, например, империческим путем, лишь бы при ω > 0 величина ε′′(ω) была положительной ε′′(ω) > 0 (это ее необходимое физическое свойство, отмеченное ранее). При этом, вычисление по формуле (7.17 или 7.19) дает функцию для ε′(ω) не противоречащую никаким физическим требованиям для нее, т.к. знак и величина ε′(ω) не ограничиваются никакими физическими условиями. Это обстоятельство и дает возможность использовать формулу (7.17 или 7.19) даже по приближенной функции ε′′(ω). Напротив, формула (7.18) при использовании в общем случае произвольной функции ε′(ω) не обеспечивает автоматическим образом положительность результата вычисления (положительность значения функции ε′′(ω) – ее основного физического свойства).
В теории дисперсии принято записывать выражение для ε′(ω) в виде
ε′(ω)
– 1 = –
 , (7.21)
, (7.21)
где e и m – заряд и масса электрона, а функция f (ω)dω (здесь x заменено на ω, ведь x это та же частота) называется силой осцилляторов в интервале частот dω. Сравнивая выражение (7.21) с (7.19) получим
f
(ω)
=
 ωε′′(ω).
(7.22)
ωε′′(ω).
(7.22)
Отметим,
у
металлов
f
(ω)
стремится к конечному пределу при ω
→ 0 (ε′′(ω)
=
 смотри (7.20) и (7.15)).
смотри (7.20) и (7.15)).
При достаточно больших значениях ω в подынтегральном выражении в (7.19) можно пренебречь x по сравнению с ω, и не писать главного значения интеграла. (В этом случае оставшееся подынтегральное выражение не имеет особенностей – функция ε′′(x) > 0 и конечная, т.е. ω больше любых собственных резонансных часто вещества.) Тогда (7.19) примет вид:
ε′(ω)
– 1 = –
 . (7.23)
. (7.23)
Выражение (7.23) дает поведение ε′(ω) при очень больших частотах. Но с другой стороны, это же поведение мы уже получили ранее, и оно описывается формулой (7.16). Так как результат должен быть одинаковым, независимо от способа его получения, то сравнение обоих выражений (7.16) и (7.23) с учетом (7.22) дает:
 =
=
 =N,
(7.24)
=N,
(7.24)
где N – полное число электронов в единице объема вещества. Соотношение (7.24) носит название – правило сумм.
Если ε′′(ω) не имеет особенности при ω = 0 (например, диэлектрики), то в формуле (7.19) можно перейти к пределу при ω → 0, и мы получим
ε′(0)
– 1 =
 . (7.25)
. (7.25)
Если же точка ω = 0 является особой для функции ε′′(ω) (проводник – металлы), то для вычисления указанного предела (ω → 0) необходимо предварительно заменить в подынтегральном выражении ε′′(ω) на
ε′′(ω)
–
 (тем
самым мы, как бы исключаем эту особую
точку у ε′′(ω),
т.к. при ω
→ 0
она равна ε′′(ω)
=
(тем
самым мы, как бы исключаем эту особую
точку у ε′′(ω),
т.к. при ω
→ 0
она равна ε′′(ω)
=
 (7.15)).
Кроме того, эта замена не меняет значение
интеграла, т.к. в результате “добавка”
тождественно равна нулю –
(7.15)).
Кроме того, эта замена не меняет значение
интеграла, т.к. в результате “добавка”
тождественно равна нулю –
 =
=
 –
–
 ,
а последний интеграл и соответственно
“добавка” равны нулю
,
а последний интеграл и соответственно
“добавка” равны нулю


 =
0.
=
0.

Для диэлектриков формулу (7.25) можно переписать в виде
ε0
– 1 =
 ,
(7.26)
,
(7.26)
где черта над ω2 обозначает усреднение с помощью силы осцилляторов:
 =
=
 .
.
Это выражение (7.26) может быть полезным при различных оценках величин ε0.
Особенность для магнитной проницаемости.
Все изложенные результаты (с небольшим видоизменением) относятся и к магнитной проницаемости μ(ω). Отличие связано прежде всего с тем, что при увеличении частоты функция μ(ω) сравнительно рано теряет физический смысл. Поскольку релаксационные процессы при установлении магнитных моментов атомов и молекул весьма велики из-за значительной массы последних, а в ферромагнетиках еще и длина волны переменного электромагнитного поля становится сравнимой (и даже меньше) с размерами доменов. Поэтому, например, применять формулы Крамера – Кронига к μ(ω) надо следующим образом. Вместо бесконечного рассматриваем конечный интервал значений ω (от 0 до ω1), простирающийся до таких частот, при которых μ еще имеет смысл, но уже перестает меняться и ее мнимую часть можно считать равной нулю; соответствующее вещественное значение μ обозначим как μ1. Тогда формулу (7.19) надо писать в виде:
μ′(ω)
– μ1
=
 . (7.27)
. (7.27)
В противоположность ε0, значение μ0 = μ(0) может быть как меньше, так и больше 1. Изменение же μ(ω) вдоль мнимой оси по-прежнему является монотонным убыванием – на этот раз от μ0 до μ1< μ0.
