
- •Тема 1. Классификация дифференциальных уравнений второго порядка в частных производных.
- •1.1 Линейное дифференциальное уравнение второго порядка в частных производных.
- •1.2 Три типа дифференциальных уравнений второго порядка в частных производных
- •1.3 Характеристические уравнения для дифференциальных уравнений второго порядка
- •1.4 Приведение дифференциальных уравнений второго порядка к каноническому виду
- •1.5 Каноническая форма дифференциальных уравнений второго порядка с постоянными коэффициентами.
- •1.6 Каноническая форма ду со многими переменными
- •Тема 2. Краевые задачи гиперболического типа
- •2.4. Электромагнитное поле в однородных средах
- •2.5. Постановка краевых задач и их редукция
- •2.6. Свободные колебания бесконечной струны (стержня)
- •Тема 3. Краевые задачи параболического типа.
- •3.1 Уравнение теплопроводности
- •3.2 Охлаждение бесконечного стержня. Формула Пуассона.
- •3.3 Охлаждение полубесконечного стержня и стержня ограниченных размеров.
- •3.. Решение неоднородной краевой задачи теплопроводности.
- •3.. Решение однородной краевой задачи теплопроводности методом разделения переменных
- •3.. Решение неоднородной краевой задачи теплопроводности методом разделения переменных
- •3.. Существование, единственность и корректность решений краевых задач теплопроводности
- •Тема IV.Краевые задачи эллиптического типа.
- •4.2. Решение одномерных уравнений Пуассона и Лапласа
- •4.3. Решение двумерных уравнений Лапласа методом разделенных переменных
- •4.4. Решение трехмерных уравнений Пуассона и Лапласа в общем случае
- •4.5. Общее решение уравнения Лапласа при наличии разрыва производной искомой функции
- •4.6. Общее решение уравнения Пуассона в двумерном случае. Математическое дополнение.
4.4. Решение трехмерных уравнений Пуассона и Лапласа в общем случае
Рассмотрим уравнения Пуассона и Лапласа для полевой функции u(x,y,z):
![]() ,
,
![]() .
.
Уравнение
Пуассона имеет ![]() .
.
Его
решение в произвольном объёме V,
включающем в себя ![]() , будем искать с помощью формулы Грина
(4.5).
, будем искать с помощью формулы Грина
(4.5).
В
этой формуле в качестве u(x,
y,
z)
возьмем полевую функцию, удовлетворяющую
уравнению Пуассона на ![]() .
Используем в качестве
.
Используем в качестве ![]() ,
где R
расстояние между любой точкой источника
и любой точкой объёма V.
При совпадении точки наблюдения с точкой
истока R=0
и условия применимости формулы Грина
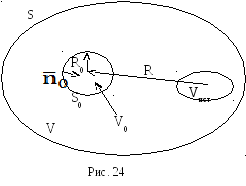
нарушаются. Окружим точку наблюдения
сферой
,
где R
расстояние между любой точкой источника
и любой точкой объёма V.
При совпадении точки наблюдения с точкой
истока R=0
и условия применимости формулы Грина
нарушаются. Окружим точку наблюдения
сферой ![]() радиуса
радиуса ![]() и выбросим область внутри сферы из
рассмотрения. (рис. 24)
и выбросим область внутри сферы из
рассмотрения. (рис. 24)
Тогда
для области ![]() формула Грина дает
формула Грина дает
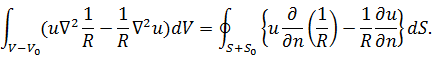
Сведем
выброшенный объем к точке ![]() .
.
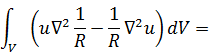
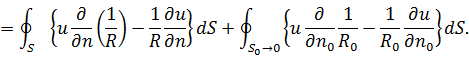
В
параграфе 4.2 было установлено, что
уравнение ![]() имеет решение
имеет решение ![]() в частном случае
в частном случае ![]() Учитывая, что
Учитывая, что ![]() =f,
имеем
=f,
имеем ![]() ,
где
,
где

Здесь
использована теорема о среднем: ![]()
Учитывая,
что ![]() совпадает с искомой функцией, находим
совпадает с искомой функцией, находим
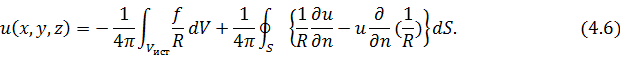
Формула (4.6) – общее решение уравнения Пуассона.
Для уравнения Лапласа при f=0 получаем
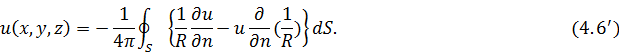
4.5. Общее решение уравнения Лапласа при наличии разрыва производной искомой функции
Б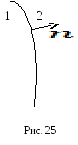 удем
считать, что искомая функция удовлетворяет
уравнению Лапласа в объёмеV,
где есть поверхность
удем
считать, что искомая функция удовлетворяет
уравнению Лапласа в объёмеV,
где есть поверхность ![]() ,
на которой производная претерпевает
скачок (рис. 25):
,
на которой производная претерпевает
скачок (рис. 25):
![]()
Выбросим
из рассмотрения точки ![]() ,
которые будем считать точками истока.
,
которые будем считать точками истока.
В
формуле Грина (4.5) выберем u
как полевую функцию, удовлетворяющую
уравнению ![]() .
.
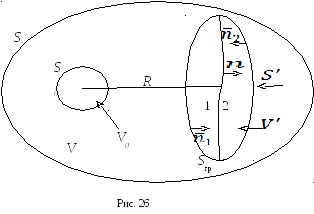
Устраним
из рассмотрения ![]() ,
,
![]() (рис. 26), получим
(рис. 26), получим
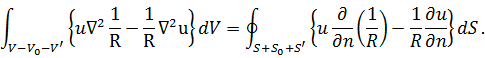
Устремляем
![]() .
.
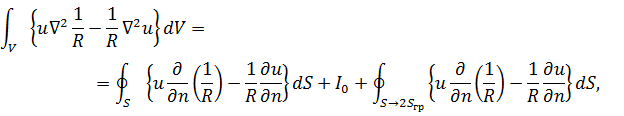
где
![]() был вычислен в параграфе 4.4:
был вычислен в параграфе 4.4:
![]()
Подсчитаем
![]() :
:
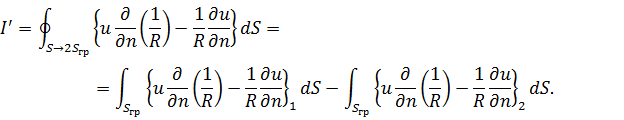
Поскольку
![]() на
на ![]() и
и ![]()
![]() получаем
получаем
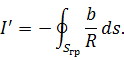
Окончательный ответ имеет вид
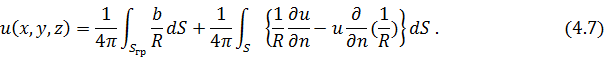
При
отсутствии разрыва производной функции
u(x,
y,
z)
внутри V
формула (4.7) переходит в (4.![]() ).
).
4.6. Общее решение уравнения Пуассона в двумерном случае. Математическое дополнение.
Т еорема
Остроградского-Гаусса в двумерном
варианте имеет вид
еорема
Остроградского-Гаусса в двумерном
варианте имеет вид
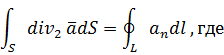
![]() – нормаль к границе области S
(рис. 27).
– нормаль к границе области S
(рис. 27).
Выбирая
![]() ,
по аналогии с выводом формул Грина в
параграфе 4.3 получим
,
по аналогии с выводом формул Грина в
параграфе 4.3 получим
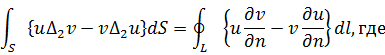
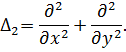
Предположим, что искомая функция u=u(x, y) удовлетворяет уравнению
![]()
![]()

В
формуле Грина будем считать u
–
искомой функцией, ![]() .
Контур
.
Контур ![]() является
окружностью радиуса
является
окружностью радиуса ![]() ,
временно исключим площадь круга
,
временно исключим площадь круга ![]() из рассмотрения (рис. 28). Тогда
из рассмотрения (рис. 28). Тогда
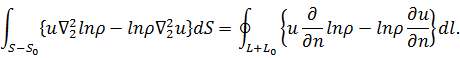
Устремим
![]()
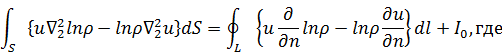
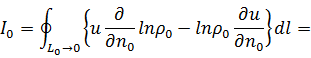
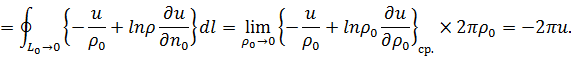
Учитывая,
что ![]() ,
получаем в результате
,
получаем в результате
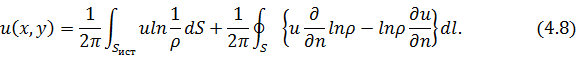
Следовательно, (4.8) является решением неоднородной краевой задачи теплопроводности на плоскости.
