Теория информации и кодирования

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №1

1. X и Y – независимые дискретные источники информации, причем источник X имеет четыре равновероятных состояния, а источник Y – три состояния с вероятностями ½ , ¼ , ¼ .

Какое среднее количество информации заключается в совместном сообщении двух источников?

Ответ:

2. X – простой источник с размером алфавита M=50 и энтропией H(X)=3 бита. Определить минимальный коэффициент избыточности равномерного двоичного кода при побуквенном кодировании.

Ответ:

3. Простой источник X имеет алфавит из 5 букв x_i, характеризующихся вероятностями

Закодировать буквы двоичным кодом Хаффмена и найти среднюю длину кодового слова.

Ответ:

4. Какой из указанных словарных алгоритмов использует метод скользящего словаря?

а) LZ77 б) LZ78 в) LZW

Ответ: а)

5. Дан порождающий полином полиномиалного кода (7,4): Является ли последовательность v’ =0100111 разрешенным кодовым словом?

Ответ: да.

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №2

1. Какова избыточность источника X с четырьмя состояниями, принимаемыми с вероятностями 1/2, 1/4, 1/8, 1/8 ? Последовательные состояния считать независимыми.

Ответ: (X)=1/8.

2. Какова средняя длина кодового слова при безызбыточном побуквенном кодировании источника без памяти с помощью неравномерного двоичного кода?

Ответ:

3. Простой источник X имеет алфавит из 5 букв x_i, характеризующихся вероятностями

Закодировать буквы двоичным кодом Шеннона-Фано и найти среднюю длину кодового слова.

Ответ:

4. Какова пропускная способность двоичного канала связи без помех, если в единицу времени по каналу передается m символов?

Ответ: m бит в ед. времени.

5. Порождающая матрица линейного блочного кода имеет вид

О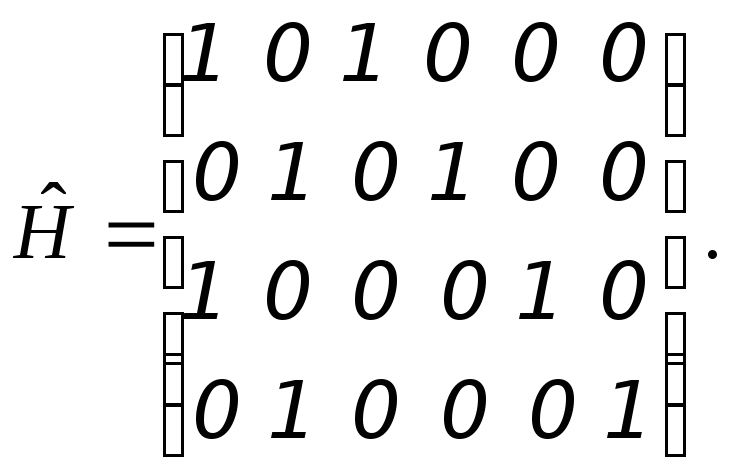пределить минимальное кодовое расстояние d_min и записать проверочную матрицу

Ответ: 3;

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №3

1. Чему равно среднее количество информации в сообщении от дискретного источника X в присутствии помех, если в результате действия помех посылаемые и получаемые сообщения оказываются статистически независимыми?

Ответ: I_ш(X)=0.

2. Какова минимальная длина l₀ равномерного двоичного кода, если кодируемый источник имеет 8 состояний?

Ответ:

3. Перечислить основные этапы работы алгоритма JPEG.

1 – Разбиение изображения на блоки данных;

2 – Применение дискретного косинус – преобразования;

3 – Округление спектральных амплитуд;

4 – Зигзагообразное сканирование;

5 – Кодирование длин повторений;

6 – Вторичное кодирование полученной последовательности.

4. Чему равна метрика Хемминга для двух двоичных последовательностей

Ответ: 1.

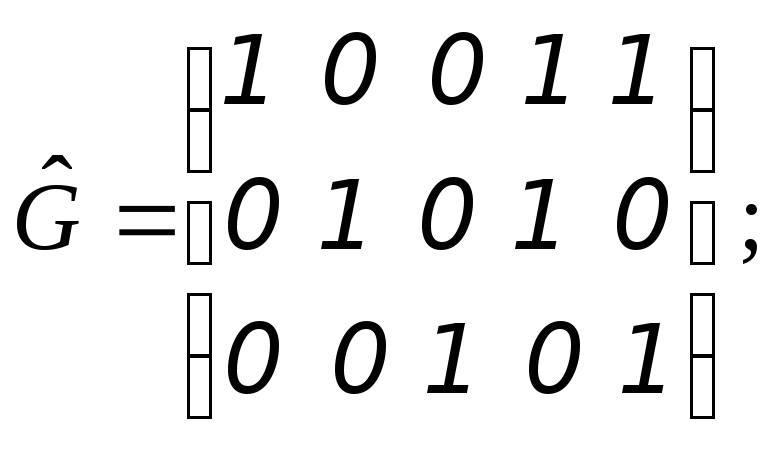
5. Проверочная матрица линейного блочного кода имеет вид

Записать порождающую матрицу и минимальное кодовое расстояние . Определить возможности кода по обнаружению и исправлению ошибок.

Ответ:

Код обнаруживает, но не исправляет ошибки кратности 1.

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №4

1. Найти дифференциальную энтропию равномерного распределения в интервале [0, 1].

Ответ: h(X)=0.

2. Может ли существовать двоичный префиксный код с вектором Крафта

Ответ: да.

3. Алфавит источника состоит из трех букв: . Закодировать методом LZW (в виде последовательности десятичных чисел) следующее сообщение:

ABAAABCCCCAAAAB.

Ответ: 1,2,1,1,4,3,3,9,6,7.

4. Чему равна пропускная способность двоичного симметричного канала с переходной матрицей

и частотой символов в канале – f_K ?

Ответ:

5. Дана порождающая матрица линейного блочного кода Хемминга

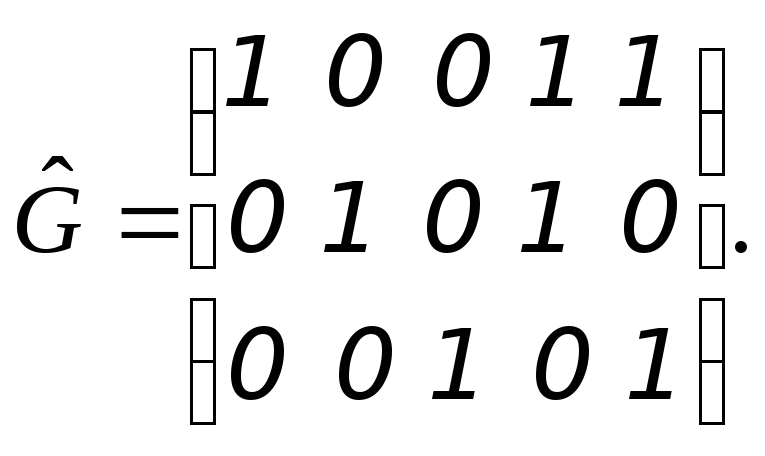
Является ли последовательность v’ =10011 разрешенным кодовым словом?

Ответ: да.

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №5

1. Какое количество информации, содержащееся в сообщении о том, что две подброшенные монеты упали на орла?

Ответ: 2 бита.

2. Является ли префиксным, код, состоящий из следующих слов: 00; 01; 001; 010; 011; 100; 101; 111 ?

Ответ: нет.

3. Закодировать число 7 -кодом Элиаса.

Ответ: 00111.

4. Какова избыточность линейного блочного кода (7,4)?

Ответ:

5. Порождающая матрица линейного блочного кода имеет вид Найти вероятность необнаруженной ошибки и вероятность неисправленной ошибки , если ошибка неправильной передачи символа в канале есть  (канал без памяти).

Ответ:

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №6

1. В двух урнах находится по 16 шаров: в первой урне 8 красных, 4 белых и 4 черных; во второй - 8 красных и 8 белых. Для какой из урн количество информации, содержащееся в среднем в результате испытания (извлечения шара) будет больше?

Ответ: для первой.

2. Найти минимальную длину l₀ равномерного двоичного кода Y, если кодируемый дискретный источник информации X имеет 7. Определить избыточность соответствующего кода (Y), считая источник X безызбыточным.

Ответ:

3. Закодировать адаптивным методом Хаффмена следующую информационную последовательность: u = CABВACС, состоящую из букв алфавита {A,B,C}.

Правило: 1) буквы выстраиваются в порядке убывания частот появления; 2) буквы с одной и той же частотой выстраиваются в порядке убывания алфавитных номеров; 3) левым ребрам кодового дерева приписывается 0, а правым – 1.

Ответ:

4. Чему равна избыточность непрерывного кода, если при поступлении каждого нового символа информационной последовательности кодер производит 3 символа кодовой последовательности?

Ответ:

5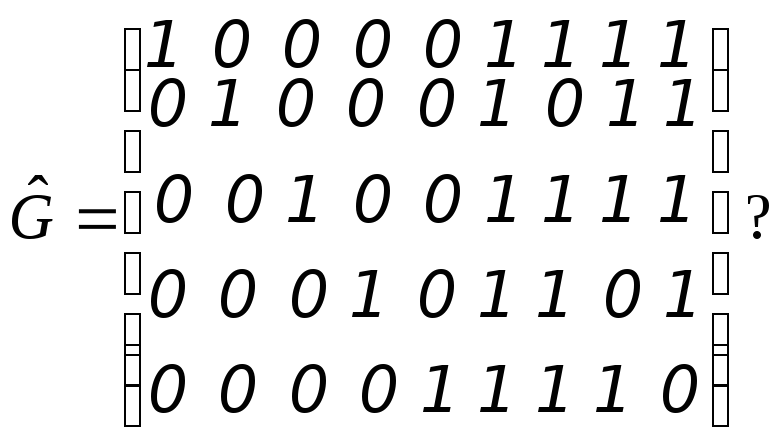. Чему равно минимальное кодовое расстояние ЛБК, задаваемого следующей порождающей матрицей

Ответ:

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №7

1. Чему равна совместная дифференциальная энтропия h(XY) двух независимых гауссовых источников с дисперсиями

Ответ:

2. Объем дискретного источника X есть M = 30. Определить минимальную длину равномерного двоичного кода Y, кодирующего X. Найти избыточность кода, если X - источник без памяти с энтропией H(X) = 2.5 бита.

Ответ:

3. С помощью алгоритма LZW декодировать следующую последовательность целых чисел v = 1,1,2,2,4,4,5,7. Алфавит источника – {0,1}.

Ответ:

4. Записать выражение для пропускной способности канала без памяти, схема которого представлена на рисунке.

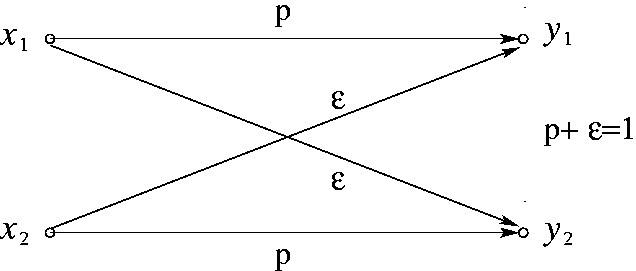
Ответ:

5. Кодовое дерево непрерывного двоичного кода представлено на рисунке. Закодировать с его помощью последовательность u= 101.

Ответ: 111000.

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №8

1. Вычислить дифференциальную энтропию равномерного распределения в интервале [0;1].

Ответ:

2. Элементарные сообщения от дискретного источника информации без памяти x₁, x₂, x₃, x₄ появляются с вероятностями 1/2, 1/4, 1/8, 1/8, соответственно и кодируются четырьмя двоичными кодовыми словами: 0, 10, 110, 111. Найти среднее число двоичных символов в расчете на элементарное сообщение и среднее количество информации в двоичном символе.

Ответ:

3. Алфавит источника Бернулли состоит из пяти букв с вероятностями Найти интервал арифметического кодирования (в десятичном представлении) для последовательности

Ответ: v[0.9628; 0.9674].

4. Чему равна метрика Хемминга для двух двоичных последовательностей: и

Ответ: d=2.

5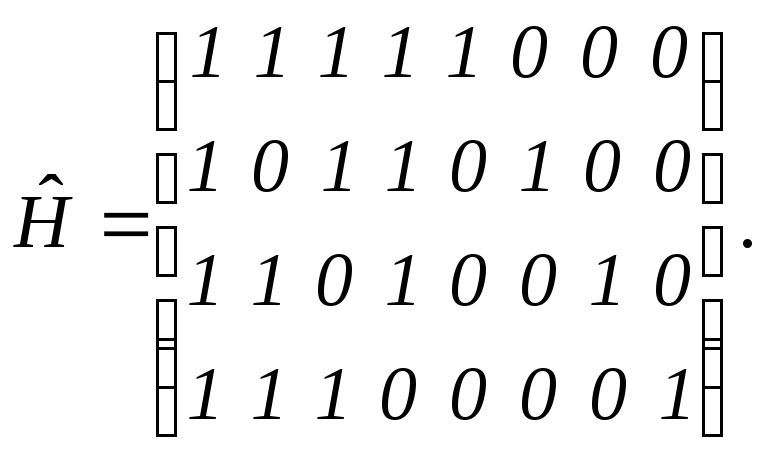. Проверочная матрица корректирующего линейного блочного кода имеет вид:

Определить возможности кода по обнаружению и исправлению ошибок.

Ответ: Обнаруживаются ошибки кратности 1, 2, 3; исправляются ошибки кратности 1.

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №9

1. Определить количество информации, содержащееся в сообщении о том, что сумма выпавших очков на двух подброшенных костях равна четному числу.

Ответ: 1 бит.

2. Сколько букв можно закодировать с помощью равномерного двоичного 8-разрядного кода?

Ответ: М=256.

3. С помощью кода LZ77 закодировать (в виде троек чисел) последовательность u=01110110111100101. Считать размер словаря и буфера неограниченным.

Ответ: v=(1,0,0)(1,0,1)(1,1,1)(4,3,0)(7,3,1)(5,1,0)(8,3).

4. Является ли канал, изображенный на рисунке каналом со стиранием?

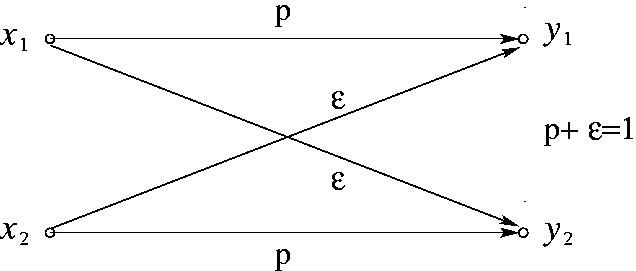
Ответ: нет.

5. Изобразить решетчатую диаграмму, соответствующую приведенному на рис.5 кодовому дереву.

Ответ:

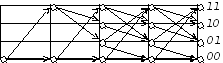
САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №10

1. Для какого распределения с заданной дисперсией дифференциальная энтропия h(X) максимальна?

Ответ: для гауссового распределения.

2. Может ли существовать двоичный префиксный код с длинами слов: 1,1,2,3,5?

Ответ: нет, т.к. не выполняеся неравенство Крафта.

3. Построить код Шеннона для источника X со следующими вероятностями состояний:

Ответ:

4. Можно ли неограниченно увеличивать пропускную способность непрерывного канала, увеличивая ширину полосы пропускания?

Ответ: нет.

5. Порождающая матрица ЛБК имеет вид Найти вероятность необнаруживаемой ошибки , если ошибка неправильной передачи символа в канале есть  (канал без памяти).

Ответ:

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени Н.Г. ЧЕРНЫШЕВСКОГО

Кафедра радиофизики и нелинейной динамики

Теория информации и кодирования

ТЕСТ №11

1. Определить количество информации, содержащееся в сообщении о том, что сумма выпавших очков на двух подброшенных костях равна двум.

Ответ:

2. Каков должен быть минимальный размер кодового алфавита, чтобы можно было закодировать равномерным кодом длиной источник с размером алфавита M=32?

Ответ: D=6.

3. Источник без памяти X принимает состояния x₁, x₂, x₃, x₄, x₅ с вероятностями 0.3, 0.2, 0.2, 0.15, 0.15, соответственно. Закодировать ансамбль состояний источника кодом Хаффмена. Вычислить среднюю длину кодового слова и найти степень сжатия кода.

Ответ:

4. Двоичный канал без памяти описывается следующей матрицей переходных вероятностей:

Определить пропускную способность канала, если средняя частота симвлов в канале есть f_K=1000 символов/с.

Ответ:

5. На рисунке представлена блок-схема двоичного сверточного кодера. Является ли сверточный код систематическим и чему равна его избыточность?

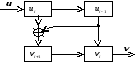
Ответ: код систематический с избыточностью (Y)=1/2.