2.9 Элементарные функции.

В таблице ниже приведены основные элементарные функции и их свойства.

Таблица 1. Свойства основных элементарных функций.

Обозначе-ние функции	Область определения X	Область значений Y	Четность, нечетность	Монотонность	Периодич-ность
y=,n	(-,)	(-,)- еслиn– нечетно; [0;), еслиn– четно	Нечетная, если n– нечетно; четная, еслиn– четно	Возрастает на (-,), еслиn– нечетно; убывает на (-,0], возрастает на (0,), еслиn– четно	Непериоди-ческая
y=,n	(-,0) (0, )	(-,0) (0,), еслиn– нечетно; [0;), еслиn- четно	Нечетная, если n– нечетно; четная, еслиn- четно	Убывает на (-,0) и на (0,), еслиn– нечетно; возрастает на (-;0) и убывает на (0,), еслиn- четно	Непериоди-ческая
y=,n,n>1	(-,), еслиn– нечетно; [0; ), еслиn- четно	(-,), еслиn– нечетно; [0;), еслиn- четно	Нечетная, если n– нечетно; общего вида, еслиn- четно	Возрастает на (-,), еслиn– нечетно; возрастает на [0;), еслиn- четно	Непериоди-ческая
y=(a>0, a1)	(-,)	(0,)	Общего вида	Возрастает на (-,), еслиа>1; убывает на (-,), если 0<a<1	Непериоди-ческая
y= (a>0, a1)	(0,)	(-,)	Общего вида	Возрастает на (0,), еслиa>1; убывает на (0;), если 0<a<1	Непериоди-ческая
y=	(-,)	[-1;1]	Нечетная	Возрастает на []; убывает на [],nZ	Период T=2
y=	(-,)	[-1;1]	Четная	Возрастает на [,], убывает на [,],nZ	Период T=
y=	(-+,+); nZ	(-,)	Нечетная	Возрастает на []; nZ	Период T=
y=	(); nZ	(-,)	Нечетная	Убывает на []; nZ	Период T=

Остальные элементарные функции получаются из основных с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции.

Сложной функцией называется функция , которая образуется из функцийи. Так, например, функцияявляется сложной, потому что образована из двух функций, где.

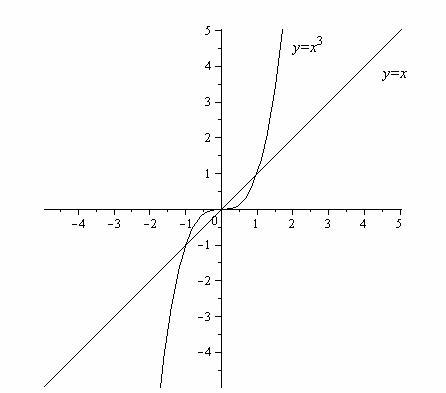
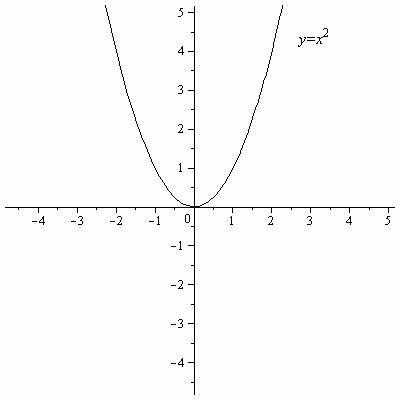
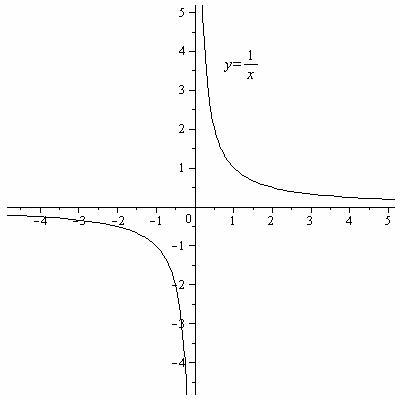
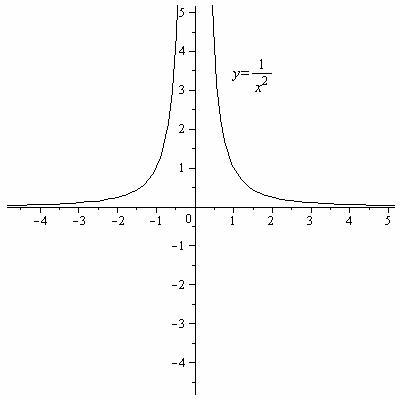
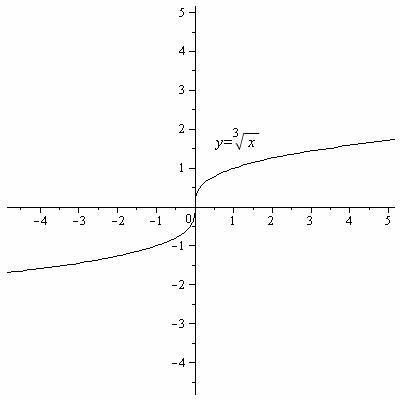
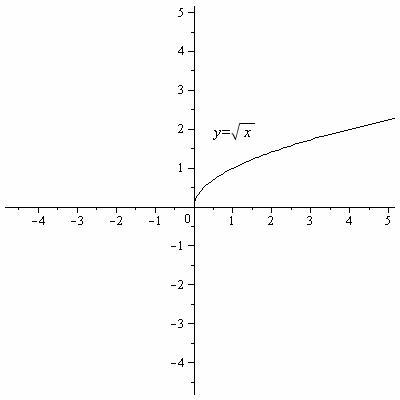
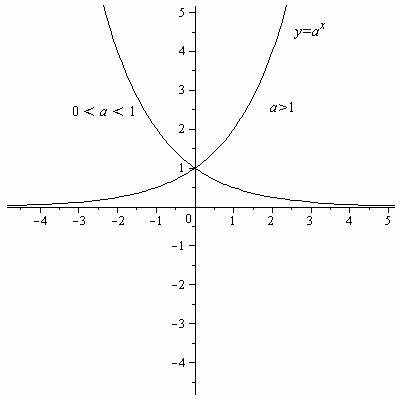
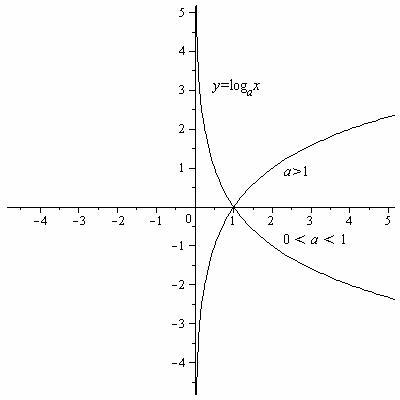
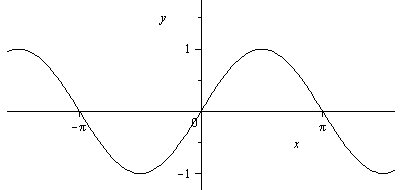
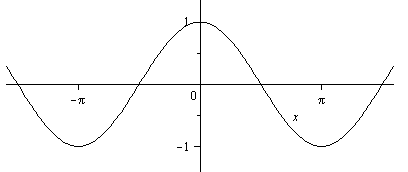
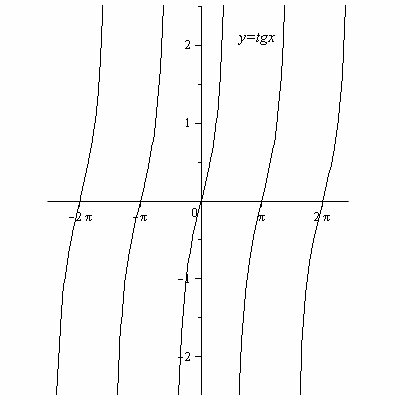
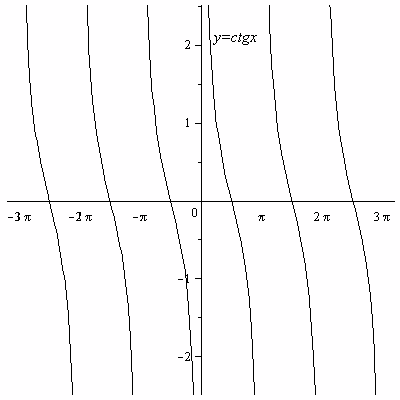
Таблица 2. Графики основных элементарных функций.

Обозначение функции	Графики функций
y=,n
y=,n
y=,n,n>1
y=(a>0, a1)
y= (a>0, a1)
y=
y=
y=
y=с

2.10. Преобразования графиков

Пусть задан график функции y=. Тогда справедливы следующие утверждения.

1.График функции y=f(x+a) есть графикy=f(x),сдвинутый (приa>0влево, приa<0вправо) на параллельноOx.

2. График функции y=f(x)+bесть графикy=f(x), сдвинутый (приb>0вверх, приb<0– вниз) на единиц параллельноOy.

3. График функции y=mf(x)( ) есть графикy=f(x),растянутый (приm>1) вmраз или сжатый(при0<m<1) вдоль оси Oy. При график функцииy=mf(x)есть зеркальное отображение графикаy=-mf(x)от осиOx.

4. График функции y=f(kx)() есть графикy=f(x), сжатый (при k>1) в k раз или растянутый(при0<k<1) вдоль осиOx. При график функции y=f(kx)есть зеркальное отображение y=f(-kx) от оси Oy.

РЕШЕНИЕ ЗАДАЧ

ПРИМЕР 1. Построить график функции

Решение.

Строим график функции следующим образом.

1. Строим график функции

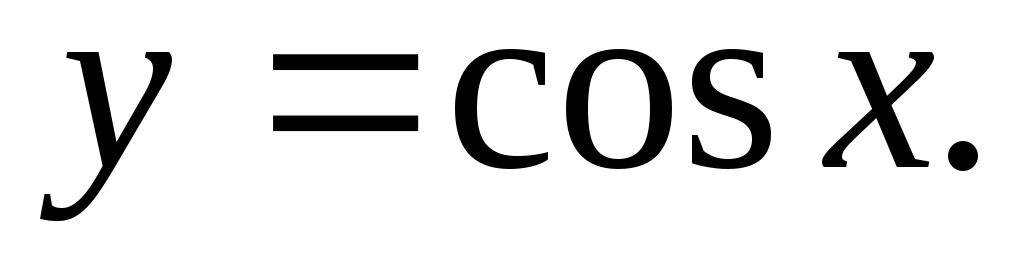
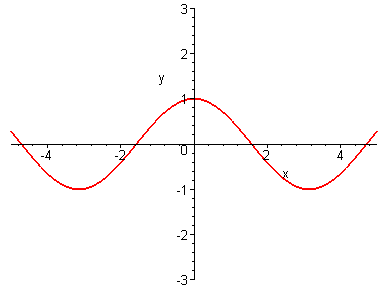
2. Сжимаем график функции в 2 раза вдоль оси Oxи получаем график

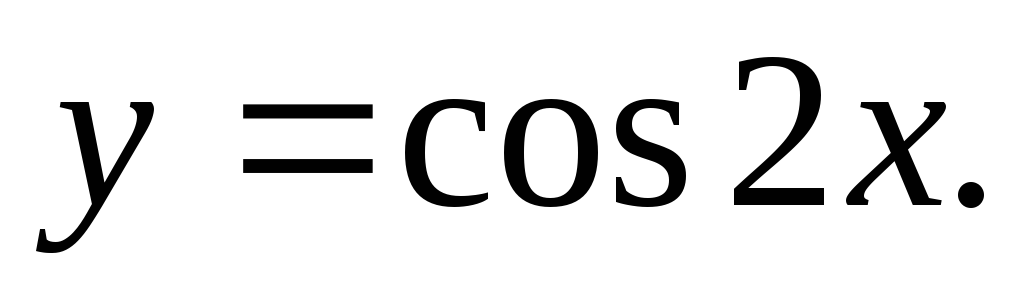
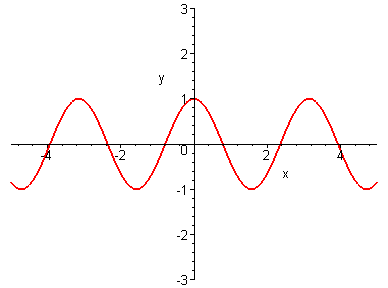
3. Зеркально отражаем график от оси Ox и получаем график

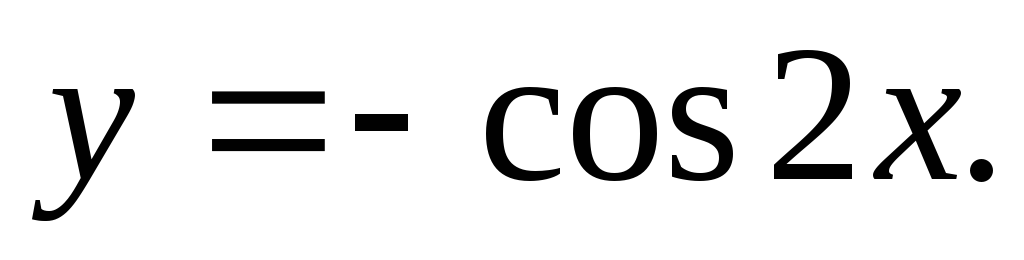
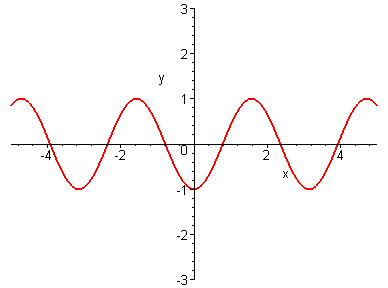
4. Растягиваем график функции в 3 раза вдоль оси Oy и получаем график

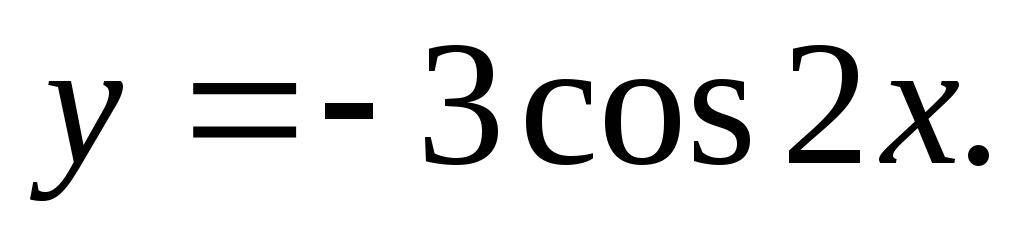
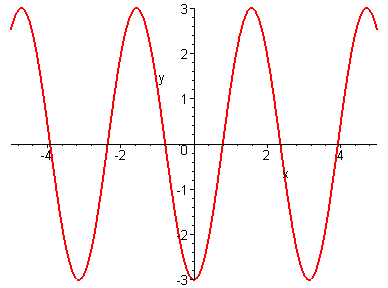
УПРАЖНЕНИЯ

Построить графики функций, используя элементарные преобразования:

2.73.

2.74.

2.75.

2.76.

2.77.

2.78.

2.79.

2.80.

2.81.

Ответы к упражнениям

2.73.2.74. 2.75.

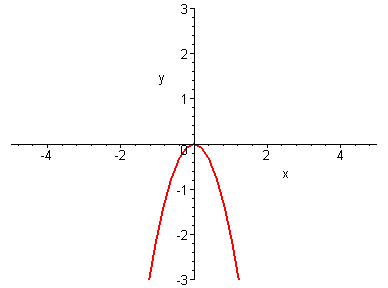
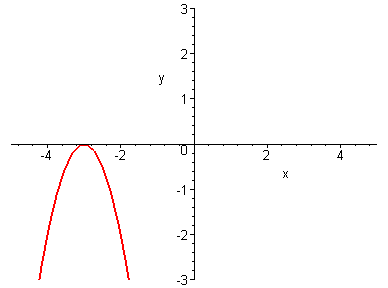
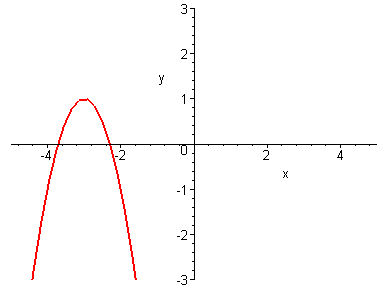
2.76. 2.77. 2.78.

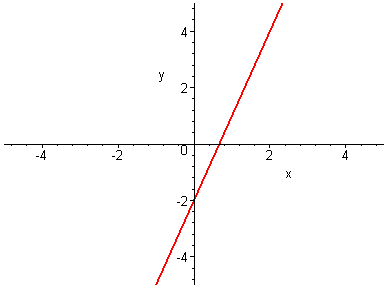
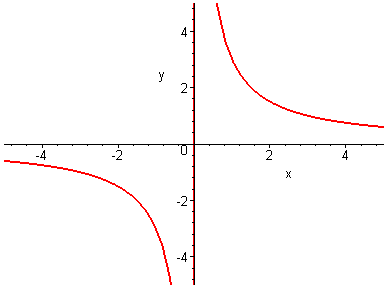
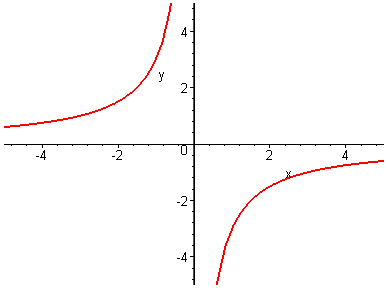
2.79.2.80. 2.81.

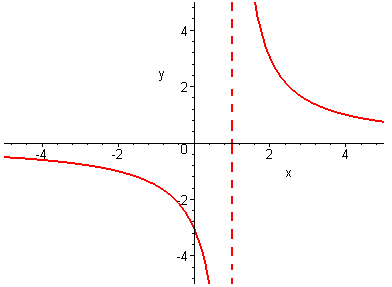
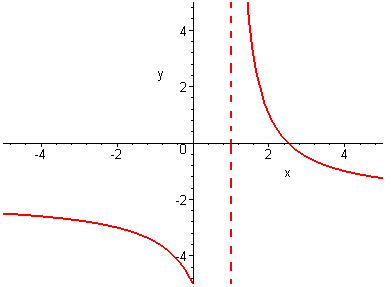
2.11. Максимумы и минимумы функции

Интервал , где >0, называется окрестностью точки .

Если функция y=f(x)определена на промежутке (a,b), то внутренняя точка этого промежутка называетсяточкой максимума функцииf(x)(точкой минимумафункцииf(x)), если существует такая окрестность точки , в которой для всехx выполняется неравенство (). Точки максимума и минимума называютсяточками экстремума.

Необходимое условие экстремума.Если в точке достигается экстремум функции, то в точке производная равна нулю или не существует.

Точки, в которых производная равна нулю или не существует, называютсякритическими точками.

Первое достаточное условие экстремума. Пусть функцияf(x)непрерывна в некоторой окрестности точки .

а) Если приx<и приx>(т.е. при переходе через производная меняет знак + на знак -), то в точке функция достигает максимума;

б) Если дляx<и дляx>(т.е. при переходе через производная меняет знак – на знак +), то в точке функция достигает минимума;

в) Если при переходе через производная знак не меняет, то в точке экстремума нет.

Второе достаточное условие экстремума. Пусть в критической точке функцияf(x)дважды дифференцируема. Если при этом , то в точке функция достигает максимума, если , то в точке достигается минимум функцииf(x).

РЕШЕНИЕ ЗАДАЧ

ПРИМЕР 1. Исследовать на экстремум функцию

f(x)= ;

Решение.

Критическими точками являются корни уравнения

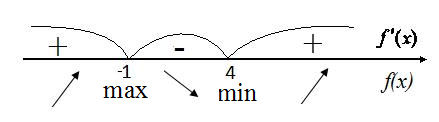
т.е. точки , . В примере 1 установлено, что:

дляx<-1

для -1<x<4, поэтому в точке = -1 достигается максимум функции

f(-1)=20.

Справедливо также неравенство:

дляx>4, поэтому в точке = 4 достигается минимум функции

f(4)= -105.

ПРИМЕР 2.Исследовать на экстремум функциюf(x)= .

Решение. Критические точки определяются из уравнения

т.е. =0, =2.

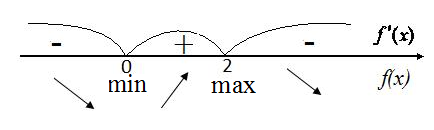
Ранее были установлены следующие неравенства:

дляx<0,

для 0<x<2,

для 2<x<+.

Таким образом, при переходе через =0 производная меняет знак с – на знак +, а при переходе через =2 со знака + на знак -, поэтому в точке =0 достигается минимум, равныйf(0)=0, а в точке =2 – максимум, равныйf(2)=0.541.

ПРИМЕР 3.Исследовать на экстремум функциюf(x)= .

Решение.

Критические точки находятся из уравнения

, отсюда = -1, =1. Так как справедливы неравенства

1+>0 для -<x<+,

1-<0 для -<x<-1,

1->0 для -1<x<1,

1-<0 для 1<x<+, то в точке =-1 достигается минимум, равныйf(-1)= -0.5, а в точке =1 максимум, равныйf(1)=0.5.

ПРИМЕР 4.Исследовать на экстремум функциюf(x)= .

Решение.

.

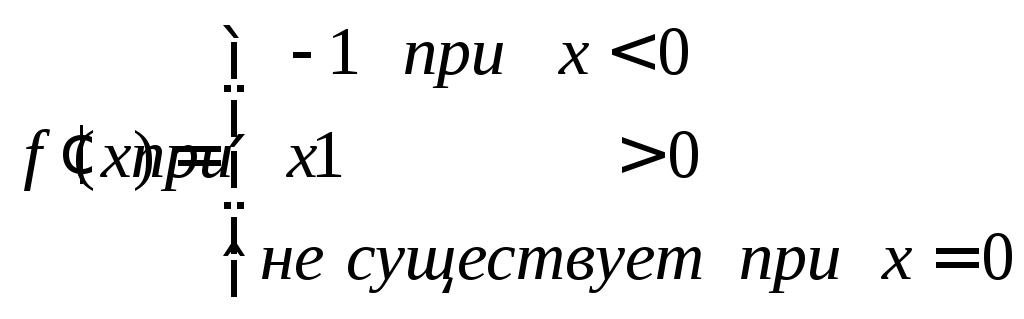Отсюда видно, что точка х=0 – точка минимума.

УПРАЖНЕНИЯ

Исследовать на экстремум следующие функции:

2.82.f(x)=ln(1-);

2.83.f(x)= ;

2.84.f(x)= ;

2.85.f(x)=x-ln(1+).

2.86.f(x)= ;

2.87.f(x)= ;

2.88.f(x)= .

2.89.

2.90.

2.91.

2.92.

2.93.

Ответы к упражнениям

2.82.Точка максимума ,f(0)= 0; 2.83.Точка максимума = 0.5,f(0.5)=24.25, точка минимума =3,f(3)= -154; 2.84. Точка максимума =1.5,f(1.5) = 0.168; 2.85.Функция монотонно возрастает, экстремумов нет; 2.86.Точка максимума =0,f(0)=1, точки минимума =2,f(2)=1, = -2,f(-2) =1; 2.87.Точка максимума =1,f(1)=1, точка минимума = -1,f(-1)= -1; 2.88.Точка минимума =,f()=.2.89.2.90.2.91.экстремумов нет.2.92..2.93.

2.12. Выпуклость и вогнутость функции. Точки перегиба

Функция f(x), определенная и непрерывная на промежутке [a,b], называетсявыпуклой (вниз), если для любых точек,[a,b] и числа , 01 выполняется неравенство

.

Функция f(x), определенная и непрерывная на промежутке [a,b], называетсявогнутой (выпуклой вверх), если для любых точек,[a,b] и числа , 01 выполняется неравенство

.

Приведенные определения имеют вполне определенный геометрический смысл. Выпуклая функция характеризуется тем, что все точки любой дуги ее графика лежат под соответствующей хордой или на ней (рис. 2.11). В случае вогнутой функции точки любой дуги графика лежат над хордой или на ней (рис.2.12).

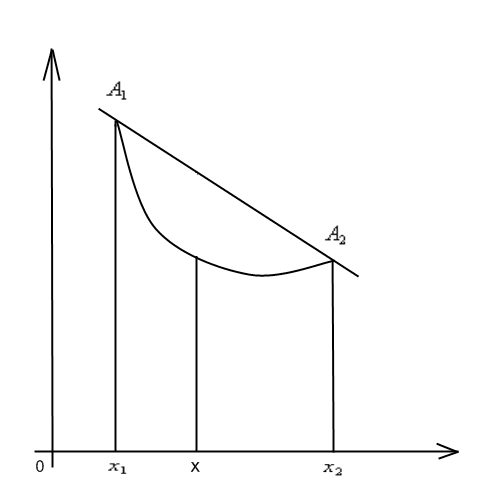
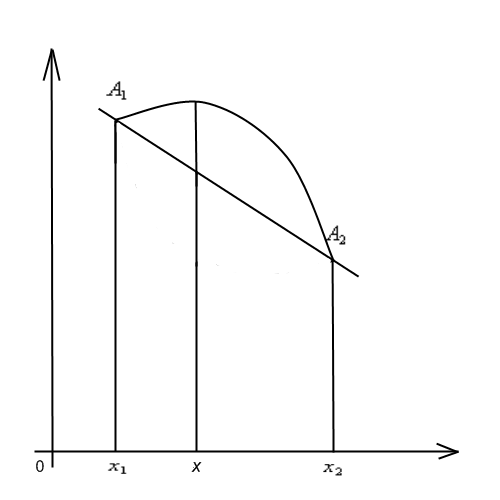
Рис.2.11 Рис.2.12

Точку (,f()) называютточкой перегибафункцииf(x), если она отделяет участок кривой, где функцияf(x)выпукла, от участка, где эта функция вогнута.

Достаточное условие выпуклости (вогнутости) функции.Если для всехx[a,b], то функцияf(x)выпукла на этом промежутке, если же для всехx[a,b], то функцияf(x)вогнута на этом промежутке.

Необходимое условие точки перегиба.Если функция f(x) дважды дифференцируемая в некоторой окрестности точкиx₀, имеет вx₀точку перегиба, то .

Достаточное условие точки перегиба.Если функция f(x) дважды дифференцируема в некоторой окрестности точкиx₀ и меняет знак при переходе через точку , то точка (,f()) является точкой перегиба функцииf(x).

Обратите внимание, что в достаточном условии точки перегиба нет требования существования второй производной в рассматриваемой точке .

РЕШЕНИЕ ЗАДАЧ

Найдем промежутки выпуклости и вогнутости, точки перегиба следующих функций:

ПРИМЕР 1.f(x)=;

Решение.Находим производные:

;

, откуда =0 при ==1.5.

Из неравенств

для -<x<1.5,

для 1.5<x<+следует, что на промежутке (-,1.5) функцияf(x)вогнутая, а на промежутке (1.5,+) – выпуклая, точка (1.5,-7.5) – точка перегиба.

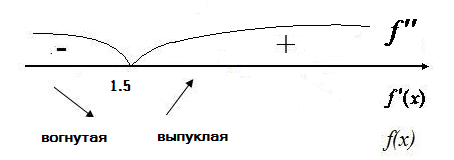
ПРИМЕР 2.f(x)=;

Решение.Находим производные:

,

, откуда при = -2, =1.5.

Решая квадратичные неравенства, находим, что

для -<x<-2,

для -2<x<1.5,

для 1.5<x<+.

Таким образом, на промежутках (-,-2) и (1.5,+) функция выпуклая, а на промежутке (-2,1.5) – вогнутая, точки (-2,-124), (-1.5,-8.0625) – точки перегиба.

ПРИМЕР 3.f(x)=;

Решение.Находим производные:

;

, откуда при =0, =, .

Знак второй производной определяется знаком величины z=x(. Так как

x(<0 для -<x<-,

x(>0 для -<x<0,

x(<0 для 0<x<,

x(>0 для <x<+, то на промежутках (-,-) и (0,) функцияf(x)вогнутая, а на промежутках (-,0) и (,+) – выпуклая. Точки (-,), (0,0) и (,) – точки перегиба.

ПРИМЕР 4.f(x)=;

Решение.Находим производные:

;. не существует. Но при этом при переходе через точку 0 вторая производная меняет свой знак с «минуса» на «плюс», значит, на интервалефункция выпукла вверх и выпукла вниз на интервале, точка 0 – точка перегиба.

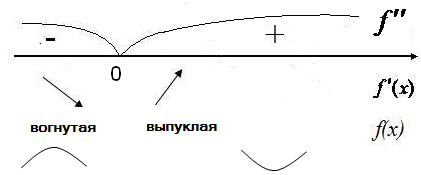
УПРАЖНЕНИЯ

Найти промежутки выпуклости и вогнутости, а также точки перегиба следующих функций:

2.94.f(x)= ;

2.95. f(x) =;

2.96. f(x) =;

2.97. f(x) = ;

2.98. f(x) =;

2.99.f(x)= ;

2.100.f(x)= ;

2.101.;

2.102.;

2.103.;

2.104.;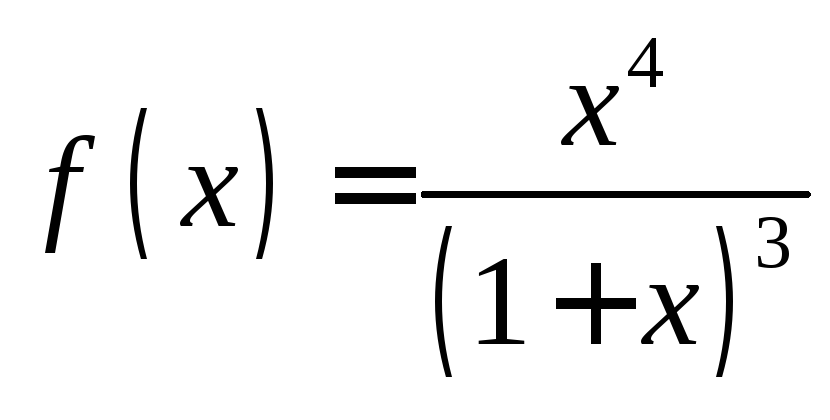

2.105.;

2.106..

Ответы к упражнениям

2.94.(-;) и (1;+) – промежутки выпуклости, (,1) – промежуток вогнутости, (;), (1;13) – точки перегиба;2.95.(-;3) – промежуток вогнутости, (3;+) – промежуток выпуклости, = (3;-162) – точка перегиба;2.96.Приx<0 кривая вогнута, приx>0 – выпукла, (0,0) – точка перегиба; 2.97.(-;-) и (;+) – промежутки выпуклости, (-;) – промежуток вогнутости, (-;-), (;-) – точки перегиба;2.98.(-;-) и (;+) – промежутки выпуклости, (-;) – промежуток вогнутости, (-;-2), (;-2) - точки перегиба; 2.99.(-;-3) и (-1;+) – промежутки выпуклости, (-3;-1) – промежуток вогнутости, (-3;), (-1;) - точки перегиба;2.100.(-;-1) и (1;+) – промежутки выпуклости, (-1;1) – промежуток вогнутости, точек перегиба нет.2.101.ответ: функция выпукла вверх на промежуткеи выпукла вниз на промежутке; точка- т. перегиба.2.102.функция выпукла вверх на промежуткахи выпукла вниз на промежутке; точки- т. перегиба.2.103.функция выпукла вверх на промежуткеи выпукла вниз на промежутке; точка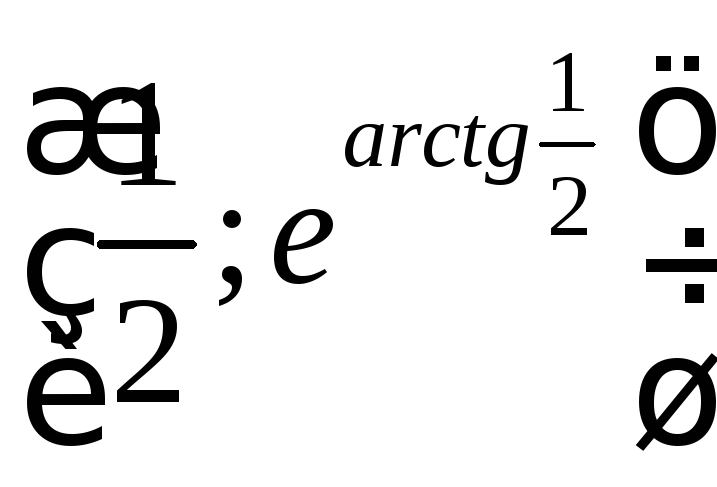- т. перегиба.2.104.т. перегиба нет; функция выпукла вверх при х<-1 и выпукла вниз при х>-1.2.105.т. перегиба .2.106.т. перегиба 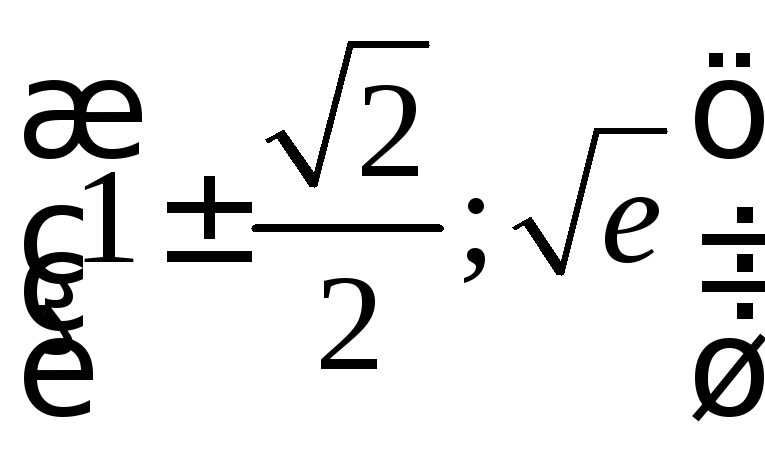; функция выпукла вверх прии выпукла вниз при.