2.3 Непрерывность функции. Точки разрыва функции

ОПРЕДЕЛЕНИЕ 1 Функцияf(x)непрерывна в точкеx₀ , если ее предел в точкеx₀ равенf(x₀) (значению функции в данной точке), т. е.

.

Иначе говоря, функция удовлетворяет следующим трем условиям:

1. определена в некоторой окрестности точки 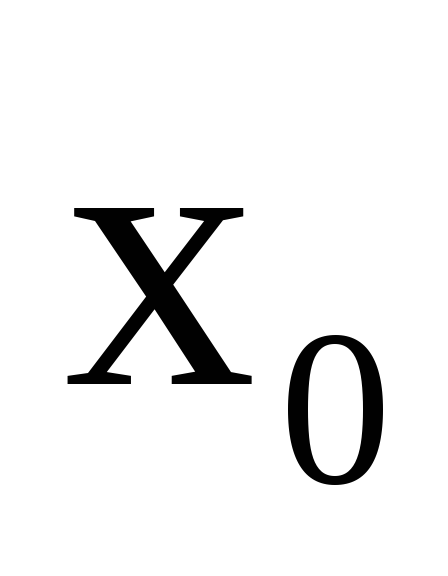(т.е. существуетf(x₀));

2. имеет конечный предел ;

3. .

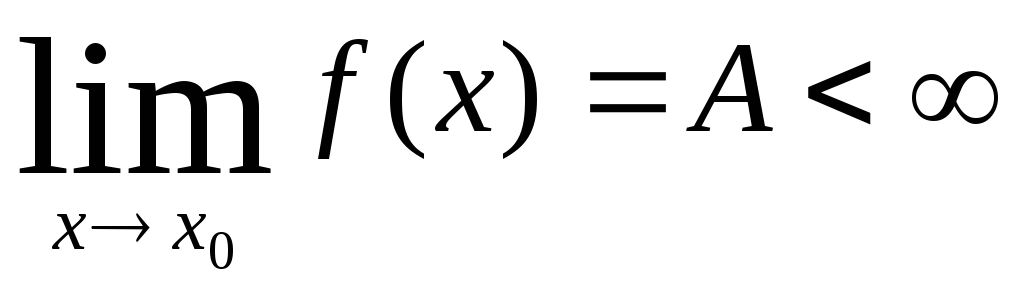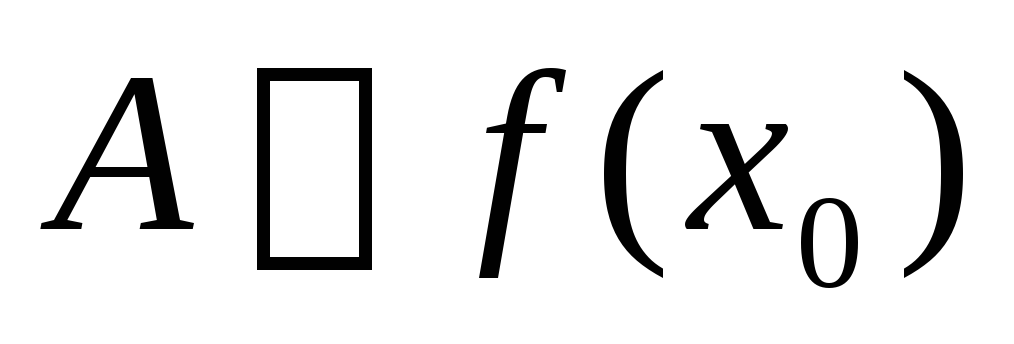Так любая элементарная функция непрерывна в каждой точке области ее определения.

Пример непрерывной функции:

y

f(x₀)+

f(x₀)

f(x₀)-

0x₀- x₀ x₀+ x

Рис. 2.1

Функция, не являющаяся непрерывной в некоторой точке, называется разрывной в этой точке (имеет или терпит разрыв в точке). Сама точка называется точкой разрывафункции.

П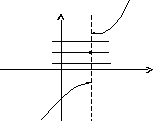ример разрывной функции:

y

f(x₀)+

f(x₀)

f(x₀)-

x₀x

Рис. 2.2

Различают точки разрыва второгоипервогорода. Точки разрывапервогорода могут быть точкамиустранимого разрыва(в точке существуют оба конечных односторонних предела, равные между собой, но не равные значению функции) инеустранимого разрыва (конечные односторонние пределы существуют, но не равны между собой). В точках разрыва второго рода хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.

РЕШЕНИЕ ЗАДАЧ

Доказать непрерывность функции в точке x₀=0 или установить характер точки разрыва в этой точке:

ПРИМЕР 1.y=.

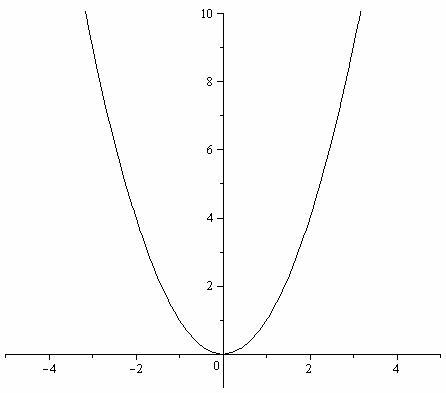
Рис. 2.3

Функция y=(рис.2.3) непрерывна в точкеx₀=0, так как она является элементарной, иx₀=0 входит в область ее определения.

ПРИМЕР 2.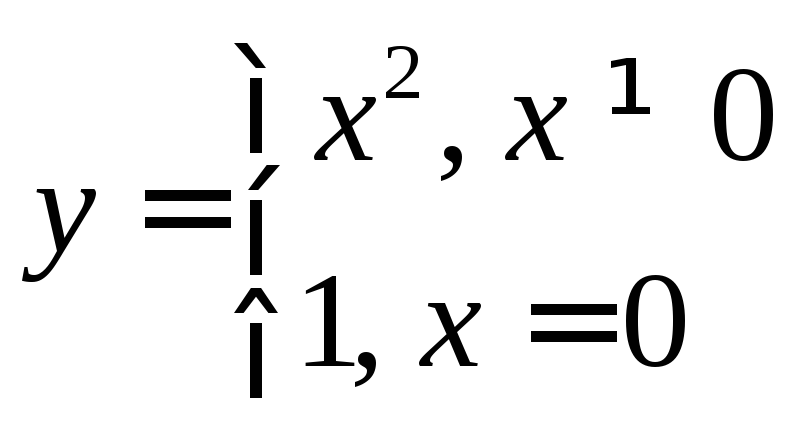

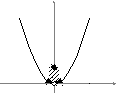
Рис. 2.4

Функция y=(рис.2.4) не является непрерывной в точкеx₀=0, т.к.не выполнено условие 3 в определении непрерывности. Точках₀=0 – точка разрыва первого рода(конечные односторонние пределы равны между собой, но не равны значению функции в точкех₀=0), причем это точкаустранимогоразрыва. Действительно,

ПРИМЕР 3. .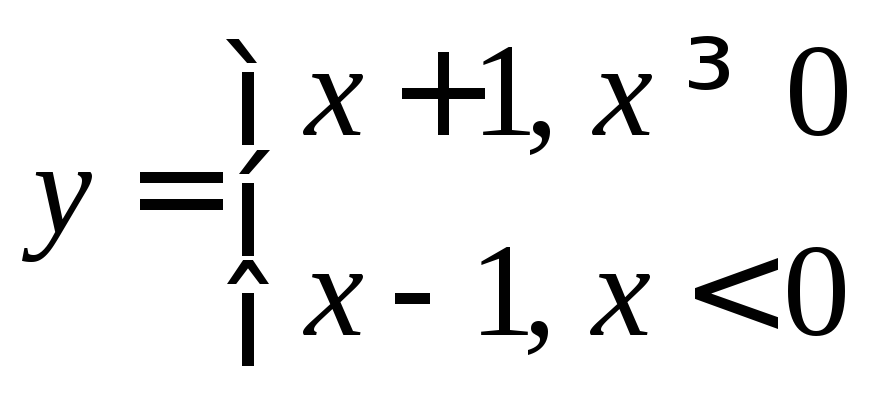

Функция y=(рис.2.5) не является непрерывной в точкеx₀=0, т.к.не выполнено условие 3 в определении непрерывности. Точках₀=0 – точка разрыва первого рода(конечные односторонние пределы существуют, но не равны между собой).

Действительно,

Такой разрыв неустраним.

Рис.2.5

ПРИМЕР 4.

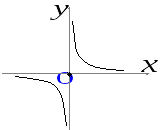
Рис.2.6

Функция y=(рис.2.6) не является непрерывной в точкеx₀=0, т.к.не выполнено условие 1 в определении непрерывности.

Для установления характера точки разрыва найдем односторонние пределы

Таким образом, точка х₀=0 – точка разрыва второго рода(оба односторонних предела равны бесконечности).

ПРИМЕР 5. .

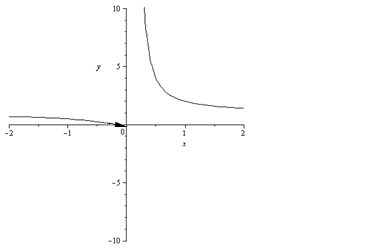
Рис.2.7

Функция y=(рис.2.7) не является непрерывной в точкеx₀=0, т.к.не выполнено условие 1 в определении непрерывности.

Для установления характера точки разрыва найдем односторонние пределы

Таким образом, точках₀=0 – точка разрыва второго рода(один из односторонних пределов равен бесконечности).

ПРИМЕР 6. .

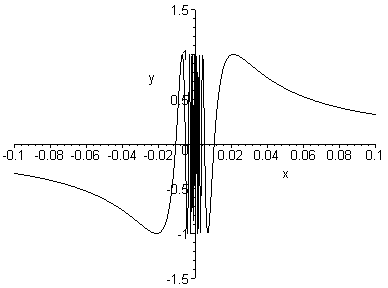
Рис.2.8

Функция y=(рис.2.8) не является непрерывной в точкеx₀=0, т.к.не выполнено условие 1 в определении непрерывности.

Кроме того,

не существуют.

Поэтому точках₀=0 – точка разрыва второго рода.

УПРАЖНЕНИЯ

Доказать непрерывность функции в точке x₀=1 или установить характер точки разрыва в этой точке:

2.26. ;

2.27. ;

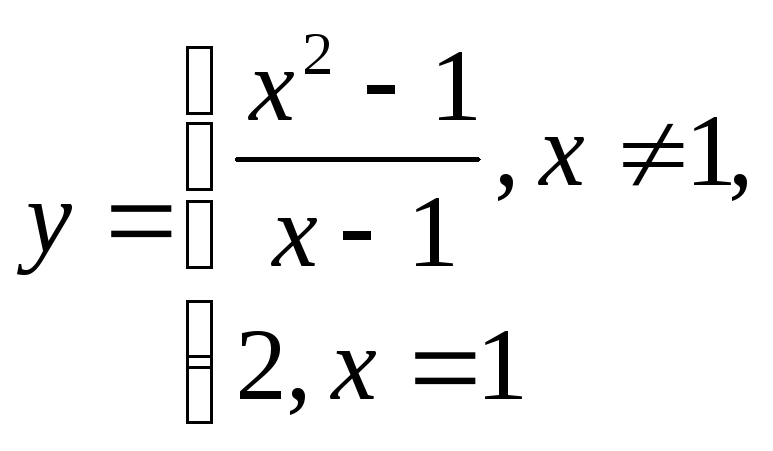2.28. ;

2.29.

При каких значениях А и В функция непрерывна?

2.30.

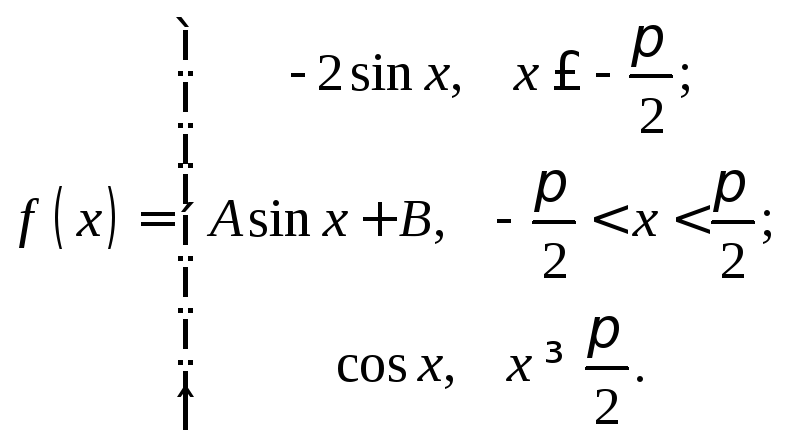
2.31.

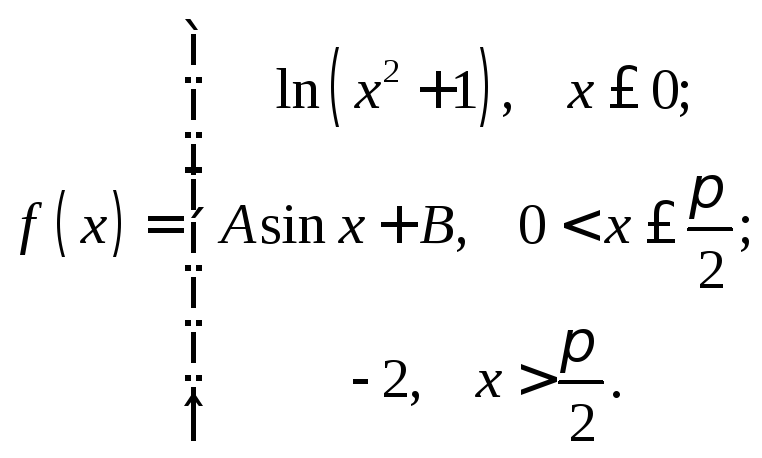
Исследовать на непрерывность и разрыв функции

2.32.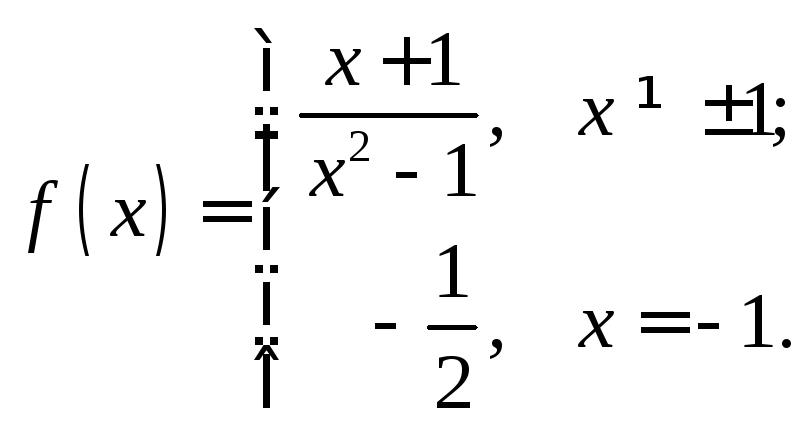

2.33.

2.34.

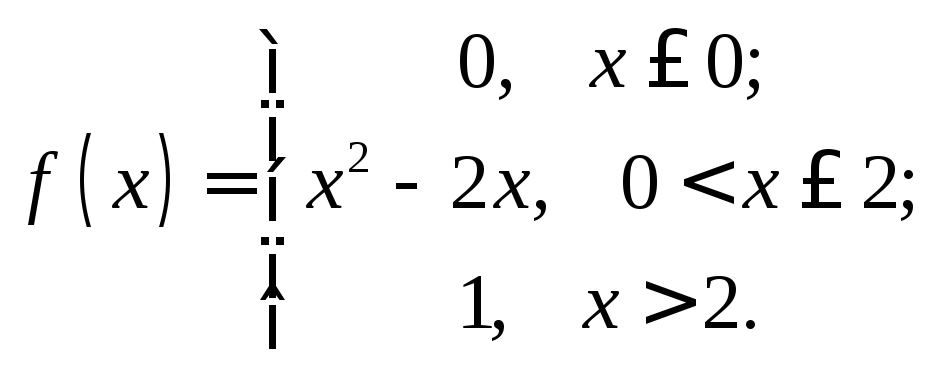
2.35.

2.36.

2.37.

2.38.

Ответы к упражнениям

2.26. x=1 – точка устранимого разрыва первого рода.2.27. Непрерывная. 2.28. х=1 – точка разрыва второго рода.2.29. x=1 – точка разрыва второго рода. 2.30. А=-1, В=1. 2.31.А=-2, В=0. 2.32. функция непрерывна во всех точках числовой оси, кроме х=1 (т. разрыва 2 рода). 2.33. функция непрерывна во всех точках числовой оси, кроме х=0 (неустранимая т. разрыва 1 рода). 2.34. функция непрерывна во всех точках числовой оси, кроме х=2 (неустранимая т. разрыва 1 рода) 2.35. х=1- т. устранимого разрыва; х=-2 – т. разрыва 2 рода.2.36. х=0 – т. разрыва 2 рода. 2.37. х=0 – т. разрыва 2 рода. 2.38. х=0 - т. устранимого разрыва.