Задача 5

Выяснить взаимное расположение двух прямых

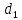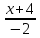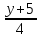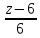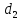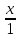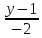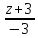: ==,:==.¹⁶

1) Вытаскиваем из уравнений точки и направляющие векторы:

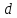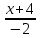: ===>(-4;-5;6),(-2;4;6)

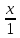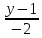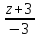: ===>(0;1;-3),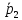(1;-2;-3)

2) Найдём вектор: 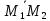 =(0-(-4);1-(-5);-3-6)=(4;6;-9)

3) Вычислим смешанное произведение векторов:

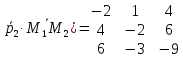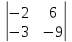(·= -2·-+4·=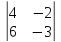

=-2·(18+18)-(-36-36)+4·(-12+12)=-72+72+0=0

Таким образом, векторы 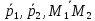компланарны, а значит, прямые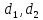лежат в одной плоскости и могут пересекаться, быть параллельными или совпадать.

4) Проверим направляющие векторы 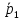(-2;4;6), 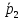(1;-2;-3) на коллинеарность.

Составим систему из соответствующих координат данных векторов:

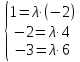
Из каждого уравнения следует, что λ= -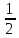, следовательно, система совместна, соответствующие координаты векторов пропорциональны, и векторы коллинеарны.

Вывод: прямые  параллельны либо совпадают.

5) Выясним, есть ли у прямых общие точки. Возьмём точку 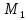(-4;-5;6) , принадлежащую первой прямой, и подставим её координаты в уравнения прямой :

= =,

-4≠3≠-3

Таким образом, общих точек у прямых нет, значит они параллельны.

Ответ: ║.

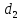Задача 6

Найти точку пересечения прямых

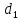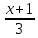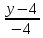: ==,:==.¹⁷

Решение:

Перепишем уравнения прямых в параметрической форме:

: ,:

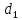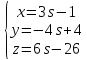
Точка пересечения прямых M(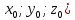принадлежит прямой 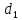поэтому её координаты 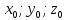удовлетворяют параметрическим уравнениям данной прямой, и им соответствуетвполне конкретное значение параметра  :

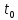M:

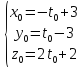
Но эта же точка принадлежит и второй прямой, следовательно:

M:

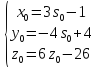
Приравниваем соответствующие уравнения и проводим упрощения:

=>

=>

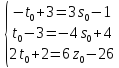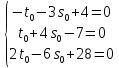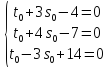
Получена система трёх линейных уравнений с двумя неизвестными. Если прямые пересекаются, то система обязательно совместна и имеет единственное решение. Из первого уравнения выразим и подставим его во второе и третье уравнение:

=> =>

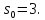
Тогда:

Подставим найденное значение параметра 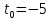в уравнения:

=> =>

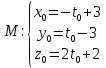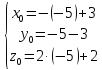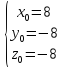
Для проверки подставим найденное значение параметра в уравнения: 

=> => =>

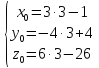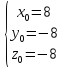
Получены те же самые координаты, что и требовалось проверить. 

Ответ: M(8;-8;-8).

Задача 7

Выяснить взаимное расположение прямых

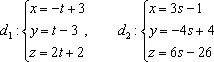.¹⁸

Решение:

1) Находим направляющие векторы и точки, принадлежащие данным прямым. Для нахождения точек удобно использовать нулевые значения параметров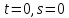: 2) Найдём вектор:  3) Вычислим смешанное произведение векторов: Таким образом, прямые 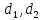могут пересекаться, быть параллельными или совпадать. 4) Исследуем направляющие векторы  на коллинеарность: , следовательно, направляющие векторы не коллинеарны, и прямые пересекаются. Ответ: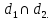

Задача 8

 Доказать, что прямые скрещиваются.¹⁹

Решение:

Найдём точки и направляющие векторы данных прямых:

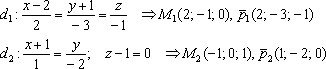
Найдём вектор: 

Вычислим смешанное произведение векторов:

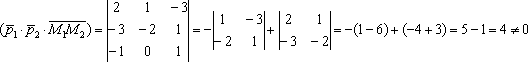
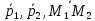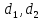Таким образом, векторы   не компланарны, а значит, прямые   скрещиваются, что и требовалось доказать.

Задача 9

В правильной четырёхугольной пирамиде ABCDS (с вершиной S) точка M — середина ребра SC. Постройте сечение пирамиды плоскостью ABM.²⁰

Решение:

Сечение изображено на рис. 10.

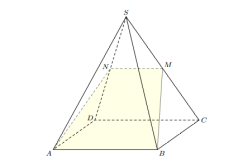
Рис. 10. К задаче

Самое главное тут — выяснить, по какой прямой секущая плоскость ABM пересекает плоскость SCD. Для этого заметим, что AB ║ CD, и по признаку параллельности прямой и плоскости имеем AB ║ SCD. А из теоремы следует тогда, что прямая MN пересечения плоскостей ABM и SCD параллельна прямой AB (и, стало быть, прямой CD).

Таким образом, MN — средняя линия треугольника SCD. Сечением пирамиды будет трапеция ABMN.

Ответ: трапеция ABMN.