Решение:

Любой многочлен из пространства 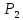имеет вид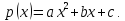Его производные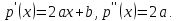Тогда условие принадлежности пространствуимеет вид:

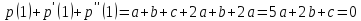, откуда

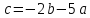, то есть общий вид многочленов из пространства

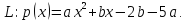
Покажем, что 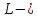линейное подпространство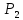. По определению подмножествоэлементов линейного пространства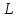называется подпространством пространства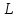, если выполнены два условия:

1)

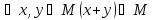
Проверим выполнение этих условий.

Пусть 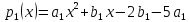и 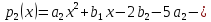два произвольных элемента из

Тогда их сумма:

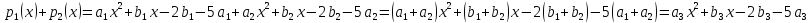тоже принадлежит множеству

Аналогично для второго свойства, пусть произвольное число,

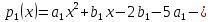произвольный элемент из . Тогда их произведение :

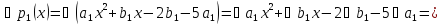
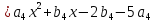тоже принадлежит множеству

Найдем базис и размерность пространства . Рассмотрим произвольный элемент из этого пространства:

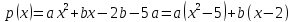, то есть он может быть представлен как линейная комбинация двух многочленов

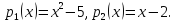
Покажем, что эти многочлены линейно независимы. Составим векторы их координат в стандартном базисе пространства 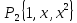. Получим вектораЭти вектора линейно независимы, так как их координаты не пропорциональны. Таким образом, многочлены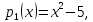

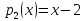образуют базис пространства 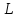, его размерность равна.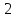

Дополним базис подпространства 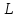до базиса всего пространства. Выберем, например, в качестве третьего базисного элемента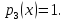Аналогичным образом проверяется, что полученные многочлены будут линейно независимы, то есть образуют базис в пространстве

Ответ: размерность,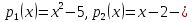базис.

Заключение

В данной курсовой работе было рассмотрено и изучено линейное подпространство, его критерии. На основе изложенного материала, была рассмотрена и решена практическая часть курсовой работы: были приведены и решены конкретные задачи по теме: «Подпространства. Критерии подпространства. Примеры».

Цели и задачи, поставленные в данной курсовой работе, были мною выполнены.

Список использованной литературы

1. Атанасян Л.С., Атанасян В.А. Сборник задач по геометрии. Часть1/ Л.С. Атанасян, В.А. Атанасян.- .Москва: «Просвещение»,1973.- 256с.

2. Апатенок Р.Ф., Маркина А.М., Нейман В.Б. Сборник задач по линейной алгебре и аналитической геометрии/, Р.Ф. Апатенок, А.М. Маркина, В.Б. Нейман.- Минск: «Высшая школа», 1990. - 243с.

3. Баврин И.И. Высшая математика. Издание шестое, исправленное / И.И.Баврин.- Москва: «Academa», 2007.-616с.

4. Базылев В.Т., Дуничев К.И., Иваницкая В.П. Геометрия. Учебное пособие для студентов 1 курса физико-математических факультетов педагогических институтов/ В.Т.Базылев, К.И. Дуничев, В.П. Иваницкая.- Москва: «Просвещение»,1974.- 352с.

5. Беклемишев Д.В.Курс аналитической геометрии и линейной алгебры. Издание девятое, исправленное/Д.В. Беклемишев.- Москва: «Физматлит», 2002.-376с.

6. Виноградова П.В., Ереклинцев А.Г. Алгебра и геометрия. Часть I. Линейная алгебра. Векторная алгебра. Аналитическая геометрия. Комплексные числа, Учебное пособие/ П.В.Виноградова, А.Г. Ереклинцев. – Хабаровск: «ДВГУПС», 2012. – 108 с.

7. Воеводин В.В. Линейная алгебра Издание второе, переработанное и дополненное/ В.В.Воеводин. - Москва: «Наука», 1980.- 400с.

8. Золотаревская Д.И. Сборник задач по линейной алгебре. Издание второе, дополненное/Д.И. Золотаревская. — Москва: «Едиториал УРСС», 2004. - 184 с.

9. Овсянников А. Я. Сборник задач по курсу линейной алгебры: Учебное пособие для студентов экономических специальностей. Издание 3-е/ А.Я. Овсянников. – Екатеринбург: «Гуманитарный университет», 2003.- 193 с.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования