Глава IV. Примеры Пример 1.

Пусть дано некоторое множество векторов в линейном пространстве. Обозначим черезсовокупность всевозможных линейных комбинаций, каждая из которых составлена из конечного числа векторов из. Множествоявляется подпространством в.¹⁰Действительно, еслии 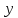принадлежаттои

где ,Мы видим, что

, т.к. также является линейной комбинацией конечного числа векторов из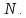Точно так же мы видим, что.

Так построенное подпространство называется линейной оболочкой множества

Пусть , ... ,- линейно независимая система векторов изтакая, что каждый вектор изпо ней раскладывается. (Если пространство конечномерно, то очевидно, что в каждом множестве, содержащем ненулевые векторы, такая система найдется.) Векторы, ... ,образуют базис в линейной оболочке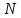. В самом деле, каждую линейную комбинацию векторов изможно представить как линейную комбинацию векторов, ...,, так как каждый вектор изможно разложить по, ... ,и подставить эти разложения в рассматриваемую линейную комбинацию.

В частности, если - конечное множество векторов, мы имеем:

Предложение 3. Размерность линейной оболочки множества из векторов не превосходит.

Пример 2

Рассмотрим однородную систему линейных уравнений с 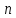неизвестными. Совокупность всех решений этой системы представляет собой подпространство в линейном пространстве столбцов высоты.

Каждая фундаментальная система решений этой системы уравнений является базисом в этом подпространстве.

Пример 3

В каждом линейном пространстве множество, состоящее только из нулевого вектора, является подпространством. Оно называется нулевым.

Пример 4

Все пространство является подпространством в

¹¹Предложение 4. Пусть подпространствоn-мерного пространства . ТогдаЕслитосовпадает с

Действительно, любая система из векторов влежит также и ви потому линейно зависима. Пусть базис всодержитвекторов. Тогда любой вектор израскладывается по этому базису и, следовательно, принадлежит. Значит,совпадает с.

Предложение 5. Пусть подпространствоn-мерного пространства . Если базис, ... ,вдополнить до базисав, то в таком базисе все векторы изи только они будут иметь компоненты

Действительно, если для вектора имеем, то

и, следовательно, . Обратно, вектор израскладывается в линейную комбинациюОна же есть разложениепо базису, ... ,при

Заметим, что равенства можно рассматривать как систему линейных уравнений, связывающую координаты вектора. Нетрудно доказать, что и в любом другом базисеопределяется системой линейных уравнений. Действительно, при замене базиса старые компоненты выражаются через новые, и в новом базисе система уравнений примет вид

, …, .

Ранг этой системы равен , поскольку строки матрицы перехода линейно независимы. Итак, мы доказали.

Предложение 6. Пусть в n-мерном пространстве выбран базис. Тогда координатные столбцы векторов, принадлежащихk-мерному подпространству удовлетворяют однородной системе линейных уравнений ранга

Глава V. Практическая часть Задача 1

Является ли подпространством линейного пространства подмножество всех верхних треугольных матриц?¹²