
- •Вопрос 1. Определение первообразной и её свойства
- •Вопрос 5.
- •Вопрос 6. Основные свойства определенного интеграла
- •Формула Ньютона – Лейбница
- •Замена переменной в определенном интеграле
- •Формула интегрирования по частям в определенном интеграле
- •Вопрос 7. Приближённое вычисление определённых интегралов
- •Вопрос 8.
- •Вопрос 9.
- •Теорема существования единственного решения - ??
- •Вопрос 10.
- •Вопрос 11.
- •Вопрос 13.
- •Вопрос 12. -?? Вопрос 14.
- •Вопрос 15.
Вопрос 1. Определение первообразной и её свойства
Пусть
функция ![]() задана
на некотором интервале
задана
на некотором интервале ![]() .
Если найдётся такая функция
.
Если найдётся такая функция ![]() ,
что при всех
,
что при всех ![]() имеет
место равенство
имеет
место равенство
![]()
то
функция ![]() называется первообразной для
функции
называется первообразной для
функции ![]() .
.
Пример 1.1
Рассмотрим функцию ![]() на
всей числовой оси
на
всей числовой оси ![]() --
на интервале
--
на интервале ![]() .
Тогда функция
.
Тогда функция ![]() --
это первообразная для
--
это первообразная для ![]() на
на ![]() .
.
Для доказательства найдём
производную от ![]() :
:

Поскольку равенство верно
при всех ![]() ,
то
,
то ![]() --
первообразная для
--
первообразная для ![]() на
на ![]() .
.
Аналогичное определение
дадим и для случая, когда функция ![]() задана
не на одном интервале, а на объединении
нескольких непересекающихся интервалов:
задана
не на одном интервале, а на объединении
нескольких непересекающихся интервалов:
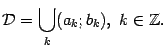
Назовём
функцию ![]() первообразной для
первообразной для ![]() ,
если при всех
,
если при всех ![]() выполнено
равенство
выполнено
равенство ![]() .
.
Правило ингрирования:
Основные
правила интегрирования.1. Вынесение
функции из-под знака дифференциала.![]() Пример:
Пример:![]() 2.
Внесение функции под знак дифференциала.
2.
Внесение функции под знак дифференциала.![]() ,
где
,
где ![]() ,
т.е. является первообразной
,
т.е. является первообразной ![]() .Пример:
.Пример:![]() [
Найдем первообразную функции
[
Найдем первообразную функции ![]()
![]() ]
]![]() Итог:
Итог: ![]()
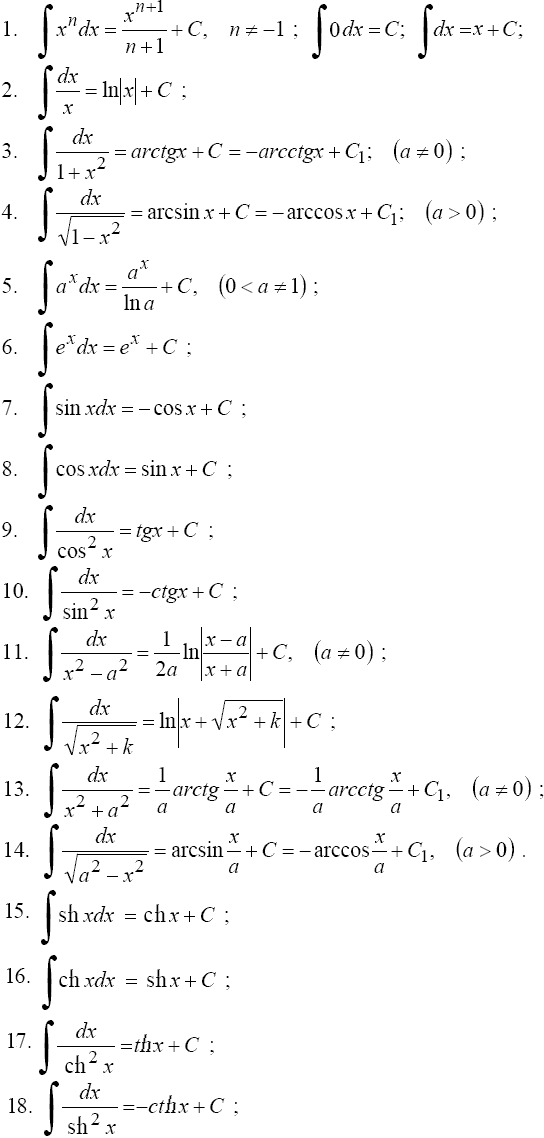
Вопрос 2.
Интегрирование путем подведения под знак дифференциала
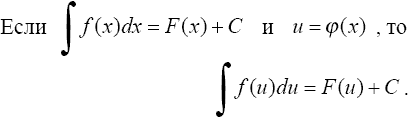
Необходимо иметь в виду простейшие преобразования дифференциала
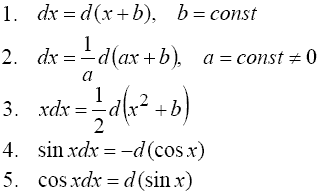
В общем случае:
'(x)dx=d(x)
Вопрос 3.
|
Интегрирование по частям |
|
|
|
Пусть u(x) иv(x) являются дифференцируемыми функциями. Дифференциал произведения функцийuиvопределяется формулой
Проинтегрировав обе части этого выражения, получим
или, переставляя члены,
Это и есть формула интегрирования по частям. |
|
Пример 1 |
|
|
|
Вычислить
интеграл Решение. Используем
формулу интегрирования по частям Следовательно, |
Интегрирование тригонометрических функций
Рассмотрим интегралы вида
![]() ,
где
,
где ![]() —
рациональная функция.
—
рациональная функция.
Такие
интегралы всегда рационализируются
подстановкой ![]() .
В самом деле,
.
В самом деле,
Выразим
далее переменную ![]() через
переменную
через
переменную ![]() .
Так как
.
Так как
![]() ,
то
,
то ![]() ,
а поэтому
,
а поэтому ![]() .
.
Значит
Таким
образом, задача свелась к вычислению
интеграла от рациональной функции.
Поскольку подстановка ![]() —
позволяет рационализировать любой
интеграл вида
—
позволяет рационализировать любой
интеграл вида ![]() ,
то её называютуниверсальной
подстановкой.
Любой интеграл этого вида выражается
через элементарные функции.
,
то её называютуниверсальной
подстановкой.
Любой интеграл этого вида выражается
через элементарные функции.
Вопрос 4.
|
Интегрирование рациональных функций |
|
|
|
Для
интегрирования рациональной функции
|
|
Пример 1 |
|
|
|
Вычислить
интеграл Решение. Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель. Получаем |
|
Интегрирование иррациональных функций |
|
|
|
Для интегрирования
иррациональной функции,
содержащей |
Найти
интеграл 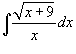 .
.
Решение.
Сделаем подстановку:
![]()
Вычислим интеграл
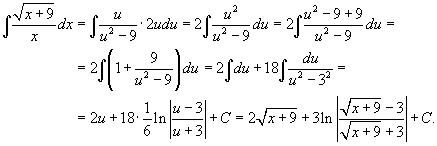

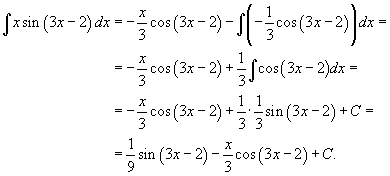
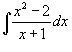 .
.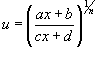 .
.