
для первого курса / для первого курса / ВЫШКА / 32. теорема о предельном переходе в равенсве и не равенсве
.pdf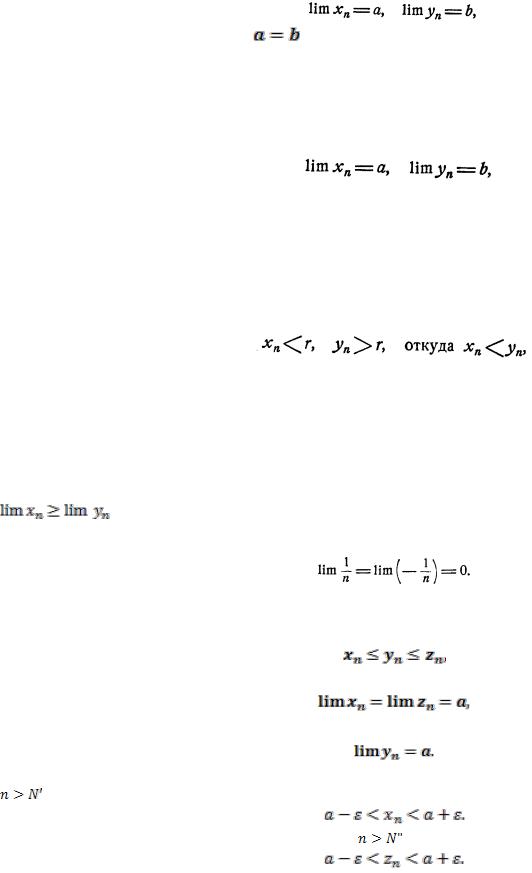
38. Предельный преход в равенстве и неравенстве. Соединяя две переменные 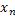 и
и 
знаками равенства или неравенства, мы всегда подразумеваем, что речь идет о соответствуших значениях их, т. е. о значениях с одним и тем же номером.
1) Если две переменные  ,
,  при всех их изменениях равны:
при всех их изменениях равны: 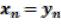 причем
причем
каждая из них имеет конечный пpeaeдел:
то равны и эти пределы: .
Непосредственно следует из единственности предела [36, 4)].
Этой теоремой пользуются обычно в форме предельного перехода в равентве: из  заключают, что
заключают, что 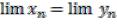
2) Если для двух переменных  всегда выполняется неравенство
всегда выполняется неравенство 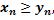 причем
причем
каждая из них имеет конечный предел:
то и 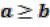 .
.
Допустим противное: пусть  . Рассуждая так же как и в пункте 36, 4), возьмем число r между а и b, так что
. Рассуждая так же как и в пункте 36, 4), возьмем число r между а и b, так что  . Тогда, с одной стороны, найдется такой номер N’, что для
. Тогда, с одной стороны, найдется такой номер N’, что для 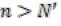 будет
будет  с друrой же найдется и такой номер N’’, что для
с друrой же найдется и такой номер N’’, что для  окажется
окажется  .
.
Если N больше обоих чисел N’, N’’, то для номеров  будут одновременно выполняться оба неравенства
будут одновременно выполняться оба неравенства
что противоречит предположению. Теорема доказана.
Эта теорема устанавливает допустимость предельного перехода в неравенстве (соединенном с равенством): из  можно заключить, что
можно заключить, что 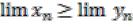 .
.
Конечно, знак всюду может быть заменен знаком
всюду может быть заменен знаком  .
.
Мы обращаем внимание читателя на то, что из строгого неравенства 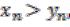 вообще говоря, не вытекает строгое же неравенство,
вообще говоря, не вытекает строгое же неравенство, 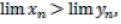 а только, по-прежнему:
а только, по-прежнему:
.
Так, например  при всех n, и тем не менее
при всех n, и тем не менее
Из теоремы 2), как частный случай, может быть получено утверждение 3) пункт 36. При установлении существования и величины предела часто бывает полезна теорема:
3) Если для nеременных  всегда выполняются неравенства
всегда выполняются неравенства
причем переменые 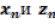 стремятся к общему пределу a:
стремятся к общему пределу a:
тo и nпеременная  имеет тот же предел:
имеет тот же предел:
Зададимся произвольным  . По этому ε прежде всего, найдется такой номер
. По этому ε прежде всего, найдется такой номер 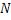 ’, что при
’, что при
Затем найдется такой номер,  , что при
, что при
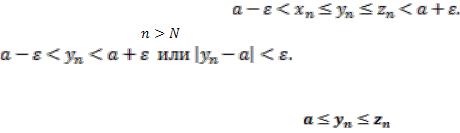
Пусть 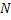 будет больше обоих чисел
будет больше обоих чисел  ; тогда, при
; тогда, при  , выполняются оба предшествующих двойных неравенства, и потому
, выполняются оба предшествующих двойных неравенства, и потому
Окончательно при
Таким образом, действительно,  .
.
Из этой теоремы в частности следует: если ,при всех n
и известно, что 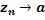 , то и
, то и  . Впрочем, это очень легко доказать и непосредственно. Теоремы 1), 2) и 3) легко распространяются и на случай бесконечных пределов.
. Впрочем, это очень легко доказать и непосредственно. Теоремы 1), 2) и 3) легко распространяются и на случай бесконечных пределов.
