Технологический расчет нефтепромысловой аппаратуры.

1. Теоретические основы теплообмена

Движущей силой теплообмена является разность температур участников данного процесса.

Цель теплообмена – выравнивание температур .

Передача тепла всегда осуществляется от более нагретого тела к менее нагретому.

Различают три вида теплообмена: теплопроводность, конвекция и излучение.

Теплопроводностью называется процесс распространения теплоты при колебательном движении частиц вещества при их взаимном соприкосновении без дополнительного перемещения.

Конвекция – это распространение теплоты с помощью переноса вещества.

Излучение – это распространение теплоты с помощью электро – магнитных колебаний.

1. Передача тепла с помощью теплопроводности.

Передача тепла от одного тела к другому с помощью теплопроводности описывается уравнением Фурье:

(492)

где: - количество теплоты, передаваемое через поверхность с постоянной температурой (стационарный режим);

- площадь поверхности, через которую передаётся тепло;

- время, в течении которого передаётся тепло;

- градиент температуры по нормали к поверхности ;

- коэффициент теплопроводности (Дж/с^.м^{. 0}С или Вт/м^{. 0}С)

Величина градиента температуры в направлении убывания температуры отрицательна. Знак «минус» в уравнении (492) показывает противоположность направлений векторов теплового потока () и температурного градиента ().

При уравнение Фурье может быть записано в виде:

(493)

где: - удельный тепловой поток или тепловая нагрузка.

Величина зависит от природы вещества и его температуры. Для металловизменяется в пределах от 10 до 500 Вт/м^{. 0}С; для неметаллов от 0,025 до 3 Вт/м^{. 0}С; для газов от 0,006до 0,6 Вт/м^{. 0}С

С ростом температуры для металлов и неметаллов уменьшается, а для газов – увеличивается.

Если в процессе передачи тепла с помощью теплопроводности температура поверхности изменяется (нестационарный режим), то в правой части уравнения Фурье добавляется сомножитель:

(494)

где: - пространственные коэффициенты;

- коэффициент температуропроводности (м²/с):

(495)

где: - удельная теплоёмкость (Дж/кг^{. 0}С);

- плотность (кш/м³);

- оператор Лапласа

Для одномерных процессов:

(496)

Передача тепла через плоскую стенку

Пусть тепло распространяется вдоль оси х, перпендикулярной плоской стенке (рис.52)

Тогда уравнение (493) можно записать в виде:

(497)

В результате его интегрирования получим:

(498)

Рис.52. Схема передачи тепла с помощью теплопроводности через плоскую стенку.

Постоянная интегрирования «с» определяется из граничных условий:

При , откуда -

Т.к. при , то:

(499)

Выразим из уравнения (498) значение удельного теплового потока :

(500)

Отношение - называется тепловой проводимостью стенки (Вт/м^{2 . 0}С), а её обратная величина- тепловым сопротивлением стенки.

Тогда, с учётом уравнения (493) при :

(501)

Наконец, с учётом уравнения (492):

(502)

Для расчета передачи тепла через многослойную плоскую стенку используют уравнение:

(503)

где: - общий перепад температуры;

- температурный перепад в -ом слое;

- число слоёв.

Пренебрегая потерями тепла:

(504)

где: - так называемый полный коэффициент теплопередачи (Вт/м^{2 . 0}С)

(505)

Передача тепла через цилиндрическую стенку

Преобразуем уравнение Фурье (492), заменив градиент температуры по нормали к поверхности на градиент температуры по радиусу:

(506)

Заменим площадь плоской поверхностина площадь поверхности трубы:

Рис.53. Схема передачи тепла с помощью теплопроводности через цилиндрическую стенку

(507)

Получим:

(508)

Запишем уравнение (508) в виде:

(509)

В результате интегрирования получим:

(510)

Постоянная интегрирования «с» определяется из граничных условий:

При , а при

Тогда:

(511)

(512)

После вычитания из выражения (511) выражения (512) и замены радиусов трубы на диаметры, получим:

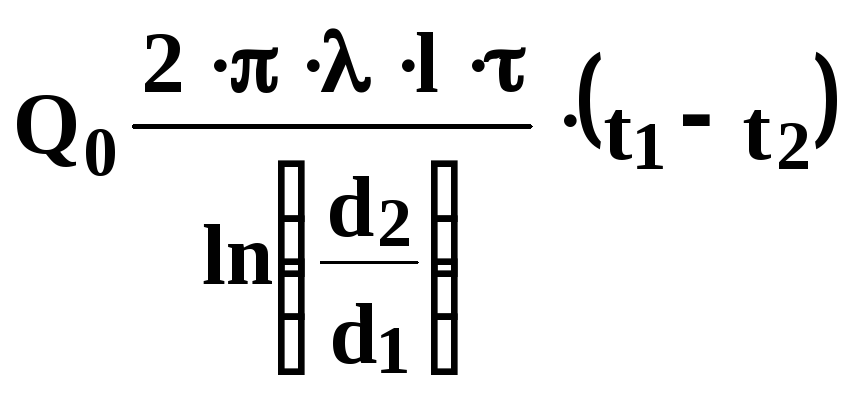(513)

Наконец, запишем формулу (513) в общепринятом виде:

(514)

Формула (514) справедлива как для передачи тепла от внутренней стенки к наружной, так и от наружной стенки к внутренней.

Если < 2, то труба считается тонкостенной и кривизна стенки слабо влияет на величину теплового потока, который в этом случае можно определять по формулам для плоской стенки.

Для цилиндрической стенки различают два вида удельного теплового потока; первый (q_s) отнесён к единице поверхности, а второй (q_l) к единице длины:

(515)

(516)

При этом, величина по аналогии сдля плоской стенки называется тепловым сопротивлением цилиндрической стенки.

2. Передача тепла с помощью конвекции.

В общем случае процесс теплопередачи с помощью конвекции описывается уравнением:

(517)

где: - средняя температура среды, отдающей тепло;

- средняя температура стенки;

- коэффициент теплоотдачи.

Если тепло передаётся от жидкости к твёрдой стенке (тли наоборот), то:

(518)

где: - средний критерий Нусельта;

- средняя теплопроводность жидкости.

Если , то:

(519)

где: - критерий Рейнольдса, определяемый по формуле:

(520)

- средняя линейная скорость жидкости;

- средняя кинематическая вязкость жидкости, м²/с (1м²/с=10^-4Ст);

- объёмный расход жидкости;

- средняя плотность жидкости;

- средняя динамическая плотность жидкости, Па^.с (1Па^.с=10 П);

- внутренний диаметр трубки;

- параметр Прандтля при средней температуре жидкости:

(521)

- средняя удельная теплоёмкость жидкости при постоянном давлении;

- параметр Прандтля при средней температуре стенки;

- параметр Грасгрофа при средней температуре жидкости:

(522)

- ускорение силы тяжести;

- коэффициент объёмного расширения жидкости;

Если , то:

(523)

Если < < , то:

(524)

Если тепло передаётся от твёрдой стенки газу (или наоборот), то:

(525)

где: - средняя линейная скорость газа.

Если тепло передаётся от твёрдой стенки к грунту (или наоборот), то:

(526)

где: - средняя теплопроводность грунта;

- наружный диаметр трубопровода;

- расстояние от поверхности земли до оси трубопровода.

Кроме рассмотренного общего подхода к определению , существует немало частных закономерностей. Например, если тепло передаётся от жидкости к твёрдой стенке (или наоборот), а< , то:

(527)

где: - длина трубки;

- параметр Пекле при средней температуре жидкости:

(528)

3. Передача тепла с помощью излучения.

В общем случае процесс теплопередачи с помощью излучения описывается уравнением Стефана – Больцмана:

(529)

где: - средняя абсолютная температура излучающей стенки;

- средняя абсолютная температура среды;

- коэффициент лучеиспускания (Вт/м^{2 .} К⁴):

(530)

- коэффициент лучеиспускания абсолютно чёрного тела (5,68 Вт/м^{2 .} К⁴);

- степень черноты тела.

4. Комбинированная передача тепла.

а) излучение – конвекция

типичным примером может служить радиантная секция печи беспламенного горения в которой тепло от раскаленной кирпичной стенки передаётся змеевику труб как за счёт излучения, так и за счёт конвективного теплообмена с дымовыми газами.

В этом случае:

(531)

или согласно уравнений ( 517) и (529):

(532)

где: - температура и абсолютная температура излучаюшей стенки;

- температура и абсолютная температура трубного змеевика.

Тогда:

(533)

Величина:

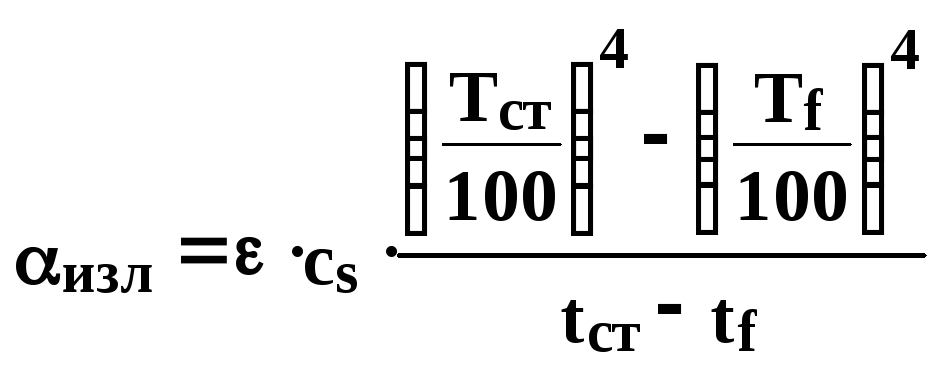(534)

называется коэффициентом теплоотдачи при излучении.

В результате:

(535)

Обозначим:

(536)

где: - общий коэффициент теплоотдачи.

Тогда:

(537)

б) конвекция – теплопроводность

Типичным примером может служить конвекционная секция любой печи в которой тепло дымовых газов передаётся через стенку трубопроводного змеевика нагреваемой среде.

Количественной характеристикой этого совместного процесса принято считать так называемый общий полный коэффициент теплопередачи ().

Для плоской многослойной стенки:

(538)

где: - коэффициент теплоотдачи от горячего потока к разделяющей стенке;

- коэффициент теплоотдачи от разделяющей стенки к холодному потоку.

Для многослойной цилиндрической стенки:

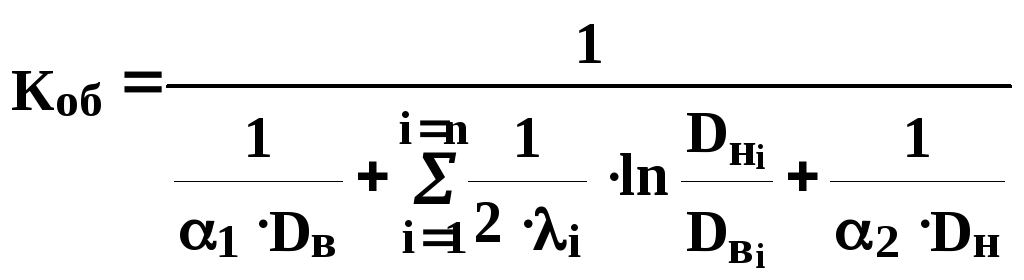(539)

Итоговая формула имеет вид:

(540)

где: - средняя температура горячего потока;

- средняя температура холодного потока.

2. Особенности передачи тепла в теплообменной аппаратуре.

При технологическом расчете любой теплообменной аппаратуры различают три типа задач:

1. Когда необходимо определить требуемую поверхность теплообмена для передачи заданного количества тепла от горячего потока к холодному;

2. Когда необходимо определить количество передающейся теплоты от горячего потока к холодному через известную поверхность теплообмена;

3. Когда необходимо определить конечную или начальную температуру горячего или холодного потока при известной поверхности теплообмена и количестве передаваемого тепла.

Во всех трёх случаях расчеты базируются на уравнении (540) и уравнении теплового баланса:

(541)

где: - массовые расходы горячего и холодного потоков соответственно;

- удельные средние теплоёмкости при постоянном давлении горячего и холодного потоков соответственно.

- начальная температура (⁰С) горячего и холодного потоков соответственно;

- конечная температура (⁰С) горячего и холодного потока соответственно.

В теплообменных аппаратах применяют четыре схемы движения потока (рис.53)

Рис.53. Схема теплобмена (t– холодный поток; Т – горячий поток)

а) прямоток; б) противоток; в) перекрестный ток; г) смешанный ток

При прямоточной схеме – горячий и холодный потоки движутся параллельно в одном направлении.

При противоточной схеме горячий и холодный потоки движутся параллельно в противоположном направлении.

Перекрестная и смешанная схема представляют собой комбинацию первых двух.

На рис.54 приведена схема изменения температур потоков при прямоточном и противоточном движении

Рис.54. Схема изменения температур потоков при прямоточном и противоточном движении

а) прямоточное течение; б) противоточное течение

Как следует из рис.54 движущая сила теплообмена (разность температур потоков) в общем случае является переменной величиной, причём, при прямотоке < , а при противотоке возможно соотношение> .

Количественно движущую силу теплообмена принято характеризовать с помощью так называемого температурного напора ().

Для прямотока:

(542)

Для противотока:

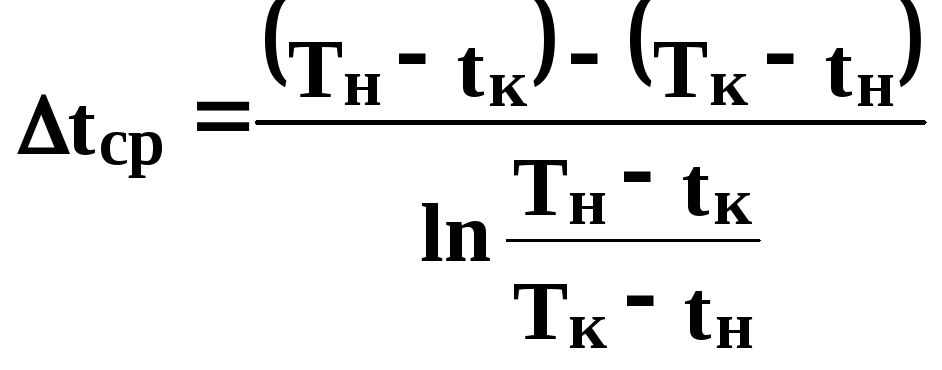(543)

В общем случае эти зависимости могут быть записаны как:

(544)

где: - большая разность температур между потоками;

- меньшая разность температур между потоками.

Причём, если: /< 2, то величину температурного напора можно найти по упрощенной зависимости:

= (+)/2 (545)

В теплообменных аппаратах принято различать так называемый эквивалентный диаметр (), определяемый для каждого типа конструкции по отдельной зависимости, например, для межтрубного пространства кожухотрубчатого теплообменника:

(546)

для теплообменников типа труба в трубе:

(547)

где: - внутренний диаметр кожуха;

- наружный диаметр трубки;

- число трубок в пучке; и.т.д.

3. Основные конструкции теплообменников

Обобщенная классификация теплообменных аппаратов может быть проиллюстрирована рис.55.

Рис.55. Классификация теплообменных аппаратов

В поверхностных аппаратах передача тепла от одной среды к другой осуществляется через разделяющую их твёрдую стенку.

В аппаратах смешения передача тепла от одной среды к другой осуществляется при их непосредственном соприкосновении.

Эффективность теплообмена выше в аппаратах смешения, а их металлоёмкость меньше, но передача тепла сопровождается нежелательным (как правило) смешением фаз.