
- •3. Плоскости
- •3.1 Положение плоскости относительно плоскостей проекций
- •3.2 Плоскость общего положения
- •3.3 Плоскость уровня
- •3.4 Проецирующая плоскость
- •Вопросы для самопроверки
- •Тест № 3
- •4. Взаимное положение прямой и плоскости
- •4.1 Принадлежность прямой линии плоскости
- •4.2 Построение прямой в плоскости
- •4.3 Параллельность прямой и плоскости
- •4.4 Построение прямой линии, параллельной плоскости
- •4.5 Перпендикулярность прямой и плоскости
- •4.6 Теорема о проецировании прямого угла
- •4.7 Условие перпендикулярности прямой и плоскости
- •4.8 Построение перпендикуляра к плоскости
- •4.9 Пересечение прямой линии с плоскостью
- •4.10 Построение точки пересечения прямой с плоскостью
- •Вопросы для самопроверки
- •Тест № 4
- •Взаимное положение плоскостей
- •5.1 Параллельные плоскости
- •5.2 Построение параллельных плоскостей
- •5.3. Пересечение плоскостей
- •5.4 Построение линии пересечения двух плоскостей (1 способ)
- •5.5 Построение линии пересечения двух плоскостей (2 способ)
- •5.6 Перпендикулярные плоскости
- •1. В заданной плоскости проведите горизонталь h и фронталь f .
- •6. Многогранники
- •6.1 Ортогональные проекции пирамиды
- •1.Спроецируйте основание пирамиды.
- •2.Спроецируйте основание пирамиды.
- •3.Спроецируйте вершину пирамиды.
- •6.2 Точка на поверхности пирамиды
- •6.3 Призма
- •6.4 Ортогональные проекции призмы
- •6.5 Точка на поверхности призмы
- •7. Поверхность вращения
- •7.1 Конус
- •7.2 Ортогональные проекции конуса
- •7.3 Точки на поверхности конуса
- •7.4 Цилиндр
- •7.5 Точка на поверхности цилиндра
- •7.6 Сфера
- •7.7 Проекции сферы
- •7.8 Точка на поверхности сферы
- •7.9 Построение проекций точкиНа поверхности сферы
- •1 Случай
- •2 Случай
- •7.10 Поверхность тора
- •Точка на поверхности тора
- •Вопросы для самопроверки
- •8.1 Метод замены плоскостей проекций
- •8.2 Четыре основные задачи преобразования чертежа
- •8.3 Метрические задачи
- •8.3.1 Определение расстояний
- •Определить расстояние от точки м до прямой [ав]
- •Определить расстояние от точки м до плоскости (авс)
- •1. Преобразуйте плоскость общего положения в проецирующую плоскость применив третью основную задачу.
- •8.3.2 Определение углов
- •Определить угол между скрещивающимися прямыми
- •1.На комплексном чертеже постройте произвольную точку а.
- •Определить двугранный угол
- •9.1 Пересечение пирамиды проецирующей плоскостью
- •9.2 Пересечение пирамиды плоскостью общего положения
- •9.3 Пересечение сферы плоскостью
- •9.4 Пересечение сферы плоскостью уровня
- •9.6 Построение линии пересечения сферы плоскостью уровня
- •9.7 Построение линии пересечения сферы фронтально проецирующей плоскостью
- •9.8 Пересечение конической поверхности плоскостью
- •Сечение - гипербола
- •3. Постройте промежуточные точки.
- •10. Пересечение прямой c поверхностью.
- •10.3 Пересечение прямой с конусом
- •10.4 Пересечение прямой с цилиндром
- •10.5 Пересечение прямой с поверхностью сферы
- •Вопросы для самопроверки
- •Тест №9
- •11. Пересечение кривых поверхностей
- •Алгоритм построения линии пересечения поверхностей.
- •Способы построения линии пересечения поверхностей
- •Способ вспомогательных секущих плоскостей
- •Способ вспомогательных секущих сфер
- •11.1 Способ вспомогательных секущих плоскостей
- •11. 2 Способ вспомогательных концентрических сфер
- •11.3 Построение проекций линии пересечения поверхностей двух цилиндров
- •Вопросы для самопроверки
- •Тест №11
Вопросы для самопроверки
1. Какие задачи относятся к 1 Г.П.З?
2. Сформулируйте алгоритм решения 1 Г.П.З ?
3. Как определяется видимость прямой в 1 Г.П.З ?
Тест №9
 1. В каком случае
прямая «а» пересекает поверхность в
четырех
1. В каком случае
прямая «а» пересекает поверхность в
четырех
точках?
 2. В каком случае
проекции 2 точек входа и выхода на П2
будут
2. В каком случае
проекции 2 точек входа и выхода на П2
будут
невидимыми?
 3. В каком случае
проекции 2 точек входа и выхода на П1
будут
3. В каком случае
проекции 2 точек входа и выхода на П1
будут
видимыми?
 4. В каком случае
проекции 2 точек входа и выхода на П2
будут
4. В каком случае
проекции 2 точек входа и выхода на П2
будут
видимыми?
11. Пересечение кривых поверхностей
В общем случае линию пересечения двух кривых поверхностей между собой строят по точкам, которые находят с помощью вспомогательных секущих поверхностей (рис.71).

Дано:
и
- криволинейные поверхности.
Построить:
линию пересечения поверхностей
и
Рис.71
Алгоритм построения линии пересечения поверхностей.
1.Проведите
вспомогательную поверхность Г.
2. Г пересекает
поверхность
по линии (KL).
3. Г пересекает
поверхность
по линии (MN).
4. Линии (KL)
и (MN)
пересекаются в точке А.
Точка А
принадлежит линии пересечения заданных
поверхностей.
5.Повторяя такие
построения многократно, с помощью «n»
вспомогательных поверхностей находят
«n»
общих точек двух поверхностей для
проведения линии их пересечения.
В качестве
вспомогательных поверхностей применяют
плоскости
и сферы,
так как
линии пересечения с заданными
поверхностями представляют собой
графически простые линии
(прямые и окружности).
Существует два
способа построения линии пересечения
поверхностей.
Способы построения линии пересечения поверхностей


Способ вспомогательных секущих плоскостей
Способ вспомогательных секущих сфер
11.1 Способ вспомогательных секущих плоскостей
Построить линию пересечения поверхности конуса с поверхностью сферы с помощь вспомогательных секущих плоскостей (рис.73). В качестве вспомогательных плоскостей применяют серию горизонтальных плоскостей, перпендикулярных оси конуса, которые пересекают сферу и конус по окружностям.


Рис. 73
Линию пересечения строят по отдельным точкам:
1. Определяют опорные точки (точки пересечения контурных линий одной поверхности с другой поверхностью).
2. Выбирают промежуточные точки.


Дано:
- конус
- сфера
= s


1. Определите
опорные точки. Точки: А – высшая, В -
низшая являются точками пересечения
фронтальных проекций очерков, так как
центр сферы и ось конуса лежат в
плоскости, параллельной плоскости П2.

2. Проведите первую
секущую плоскость
через экватор сферы.
3.
пересечет конус
по окружности «m»
(радиус показан фигурной скобкой).
4.
пересечет сферу по экватору «n».
5. Пересечение «m»
и «n»
даст точки C
и D
искомой линии пересечения. Горизонтальные
проекции этих точек являются границами
видимости участков линии пересечения
на этой проекции.
=
m
=
n
m
n = C,
D



6. Новую секущую
плоскость
I
, проведите выше экватора, но ниже точки
А.
=
a
=
b
a
b = 1,
1I
Точки 1 и 1I
являются промежуточными.


7. Третью секущую
плоскость
II
, проведите ниже экватора, но выше
точки В.
=
с
=
d
c
d = 2,
2I
Точки 2 и 2I
являются промежуточными.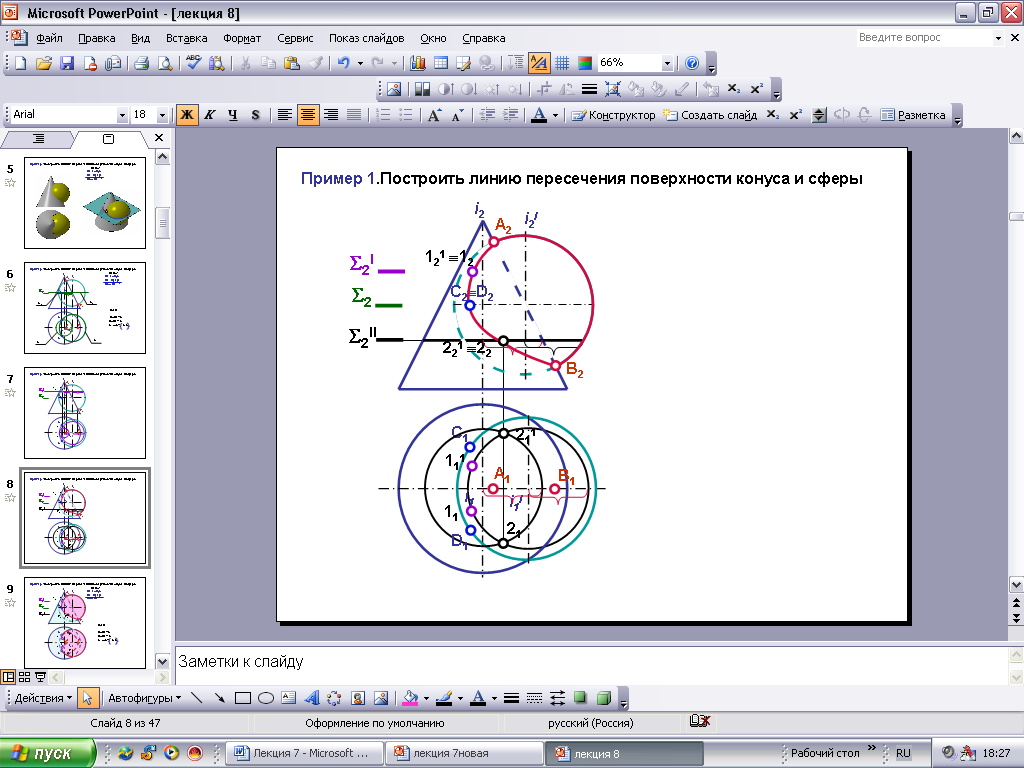



8. Соедините
полученные точки плавной линией с
учетом видимости.
s=
(A-1-D-2-B-2I-
C-1I
–A)
