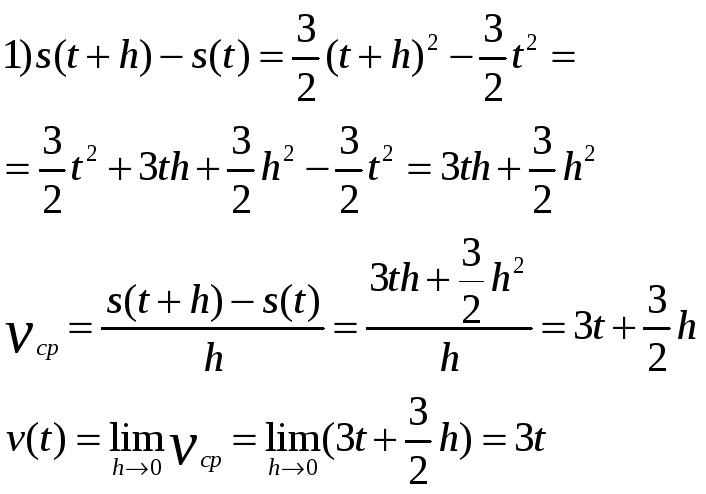Алимов урок
..docОпределение производной
10 класс.
Продолжительность занятия: 40 минут.
Тип урока: закрепления изученного материала.
Цели урока:
- Обучающие: обобщить полученные знания по теме: Производная и ее геометрический смысл.
- Воспитательные: воспитание ответственного отношения к учебе, воли и настойчивости для достижения конечных результатов.
- Развивающие: побудить интерес к изучению математики.
Оборудование: Доска, мел, линейка, учебник Аимов «Алгебра 10-11».
План урока:
1. Организационный момент (2 минуты);
2. Актуализация знаний (8 минут);
3. Закрепление изученного материала. (25 минут);
4. Итоги урока (2 минуты);
5. Домашнее задание (3 минуты);
Ход урока.
|
Этапы урока |
Деятельность урока |
Деятельность учеников |
|
№1 Организационный этап. |
Приветствую учеников. Отмечаю отсутствующих. Объявляю тему и цель урока.
|
Приветствуют учителя. Садятся на места. Дежурный называет отсутствующих. Записывают тему урока. |
|
№2 Актуализация знаний. ( Фронтальная форма работы). |
Устный опрос. 1) Что называют производной? 2)
Перечислите мне основные свойства
функции
|
Отвечают на вопросы. 1)
Отношение
называют
разностным отношением, а его предел
при
и
обозначают
2) 1. Область определения – множество всех действительных чисел
2.
Множество значений – множество
3.
Функция
4.
Функция
5.
Функция
-
положительное значение на интервалах
-
отрицательное значение на интервалах
6.
Функция
|
|
№3 Закрепление изученного материала. (Групповая форма) |
Класс делиться на три группы, в каждую группу входят как сильные ученики, так и средние со слабыми. Задание №1 Для 1-группы учеников. Найдите
производную функции
Для 2-группы учеников. Найдите производную функции
Для 3-группы учеников. Найдите производную функции
Алгоритм записан на доске. Задание №2 Для 1-группы. № 778, 780(1,2). Для 2-группы. №777, 779. Для 3-группы. №776, 782.
По ходу решения заданий представитель каждой группы выходит к доске и записывает полученное решение. Остальные ученики работают с доской и проверяют решение. После окончания занятия все ученики сдают тетради на проверку учителю. |
Приступают к выполнению заданий по группам. Группа №1
Задание №1 Найти
производную функции
Применяя определение производной, получаем
Умножим
числитель и знаменатель на
Заметим,
что
Тогда
Задание №2 № 778. Найти мгновенную скорость движения точки если: 1)
Решение: 1)
2)
Задание №2 №
780(1,2).
Используя определение производной
найти
1)
1)
2)
Группа №2
Задание №1 Найти
производную функции
Решение:
Задание №2 № 777. Найдите среднюю скорость движения точки на отрезке [1;1.2], если закон движения задан формулой
Решение: 1)
2)
№ 779. Закон движения задан формулой
1) Среднюю скорость от t=4 до t=8 2) Скорость движения в моменты t=4 и t=8. Решение:
Группа №3
Задание №1 Найти
производную функции
Решение: Используя определение производной, получаем
Применим тригонометрическое тождество
Тогда
Первый предел в данном выражении равен
Поскольку
то
для производной синуса получаем
окончательное выражение:
Задание №2 №
776.
Точка движется по закону
1) от t=1 до t=4; 2) от t=0,8 до t=1 Решение:
Поэтому
№782.
Найти
мгновенную скорость движения точки,
если закон ее движения
1)
Решение:
|
|
№4 Итоги урока. |
Спрашиваю у учеников достигли ли мы цели сегодняшнего урока? Выставляю оценки представителям групп отвечающим у доски. |
Отвечают на поставленные вопросы. Подают дневники на роспись. |
|
№5 Домашнее задание. |
Пункт 44 повторить. №783, 784, 785. Номера аналогичные решенным в классе. |
Записывают в дневники домашнее задание. |

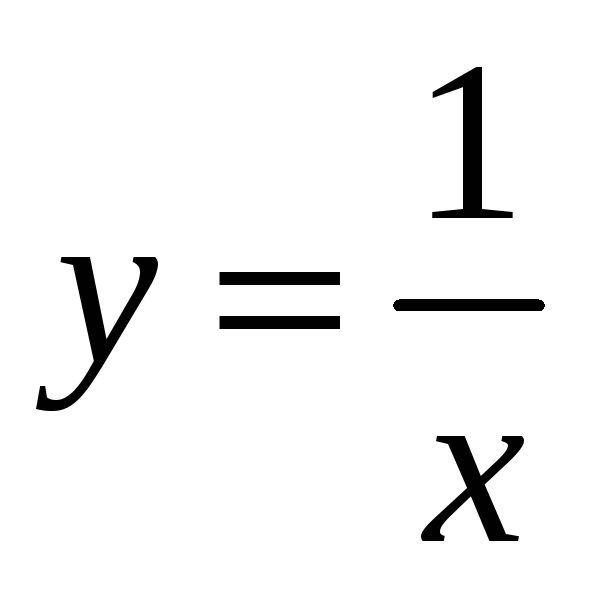 исходя
из алгоритма отыскания производной.
исходя
из алгоритма отыскания производной.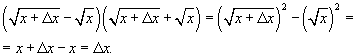

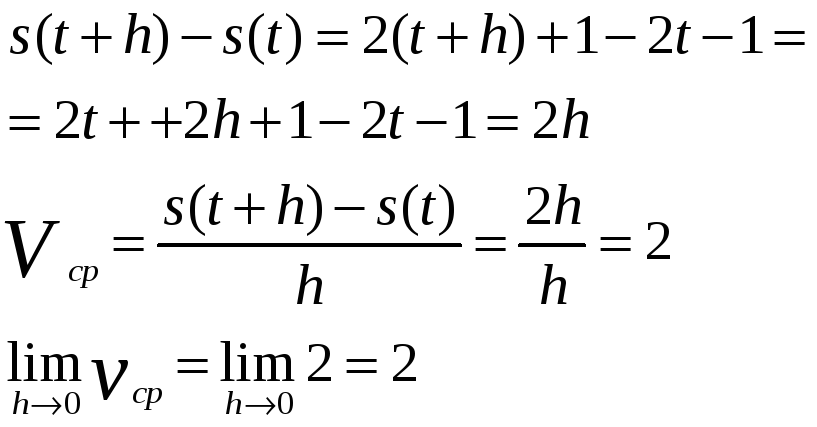
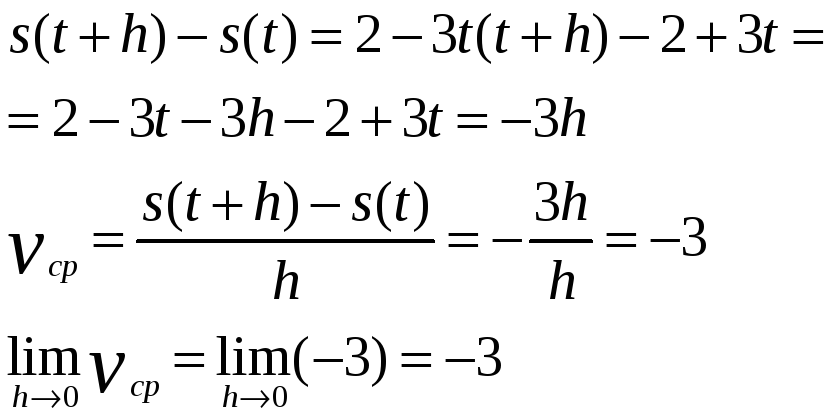
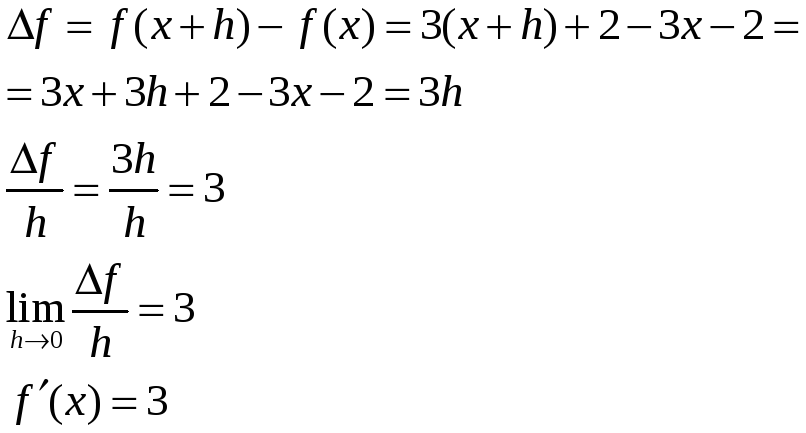
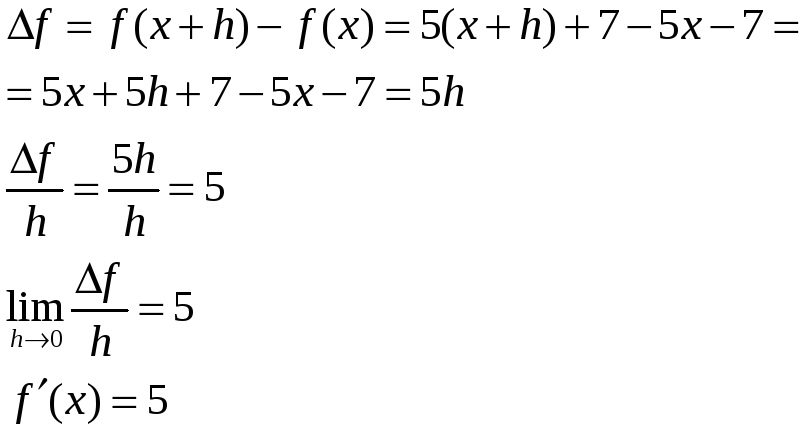
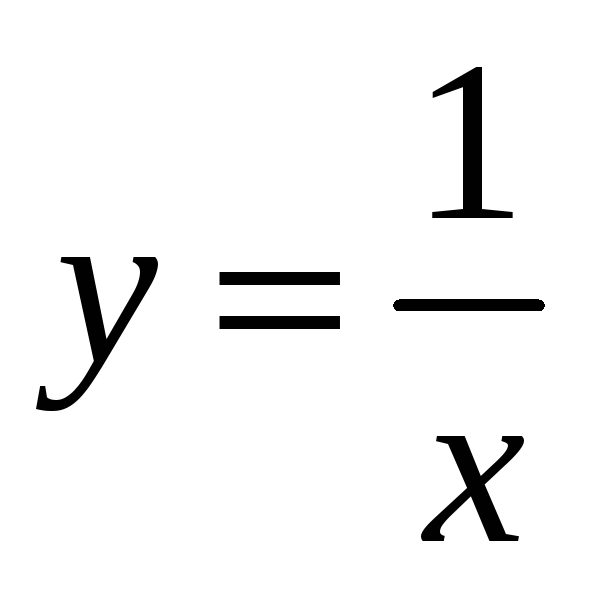
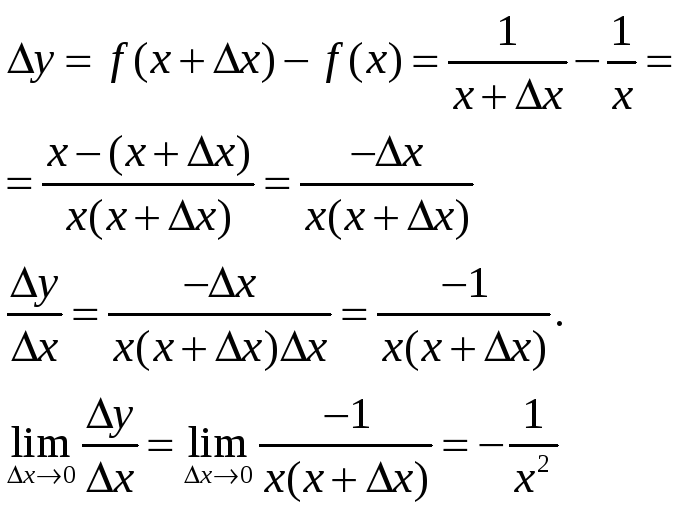

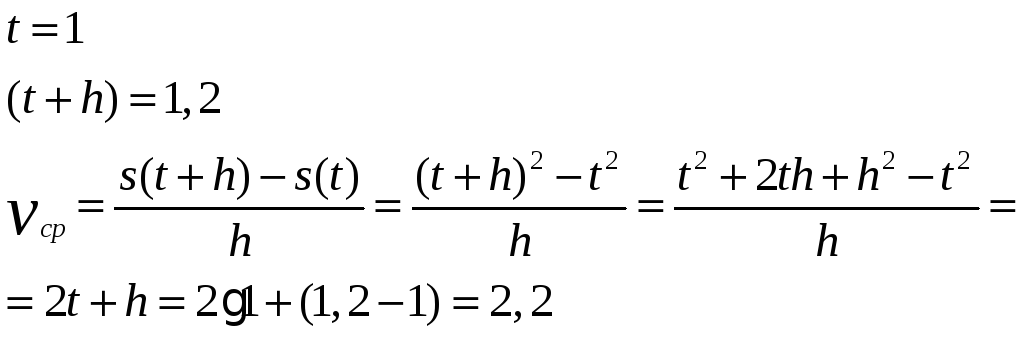
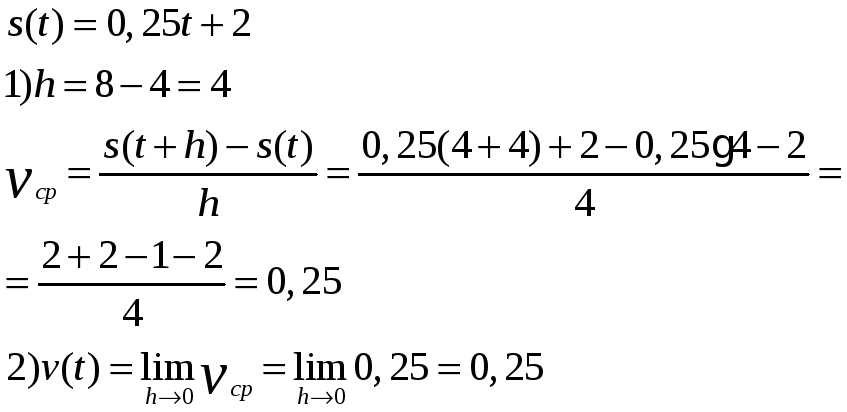
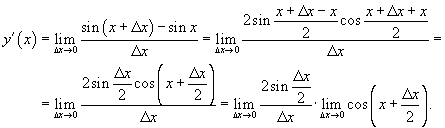
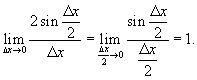
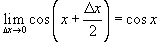 ,
,
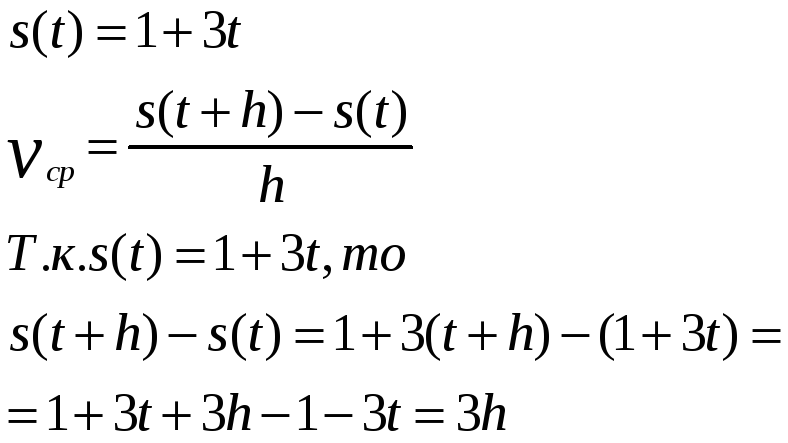
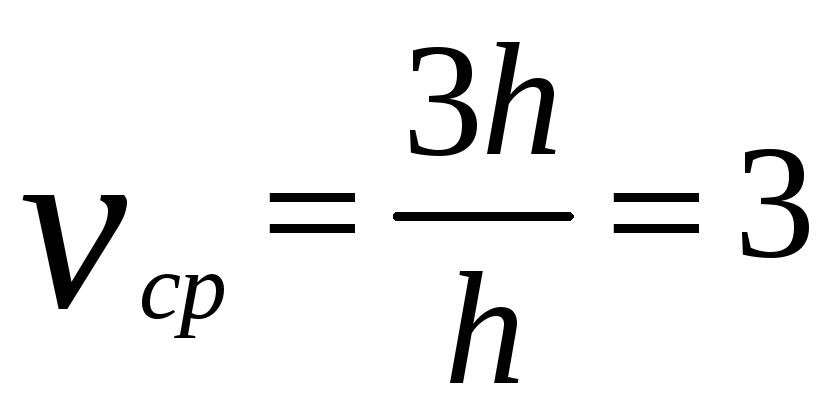 .
Проверим
результат в случаях, приведенных в
условие.
.
Проверим
результат в случаях, приведенных в
условие.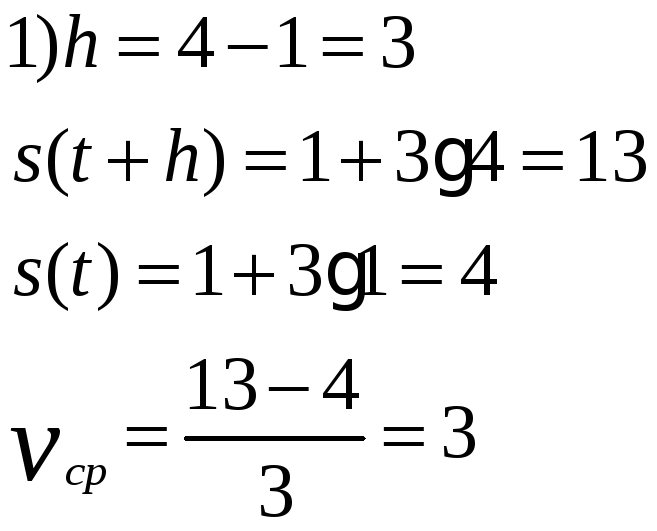
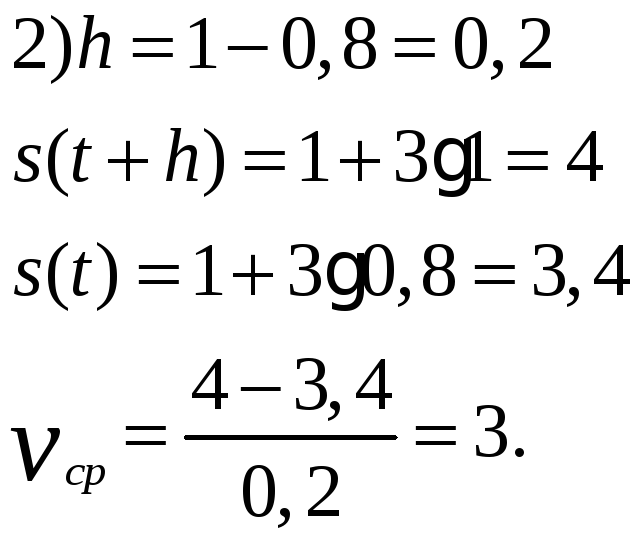
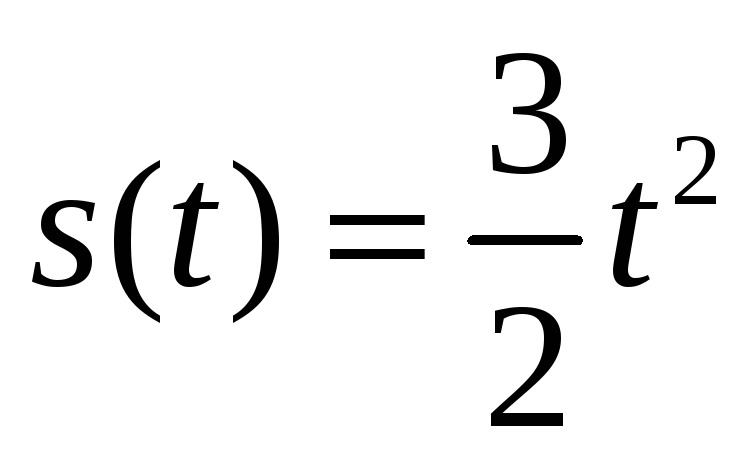 2)
2)