
Экзамен, геом, 8б, 2012-2013 по Александрову
.docЭкзаменационные билеты по геометрии
для 8 класса (с углубленным изучением предмета).
Билет 1.
-
Признаки параллелограмма с доказательством.
-
Зависимость между стороной правильного многоугольника и радиусом описанной и вписанной окружности. (Вывод формулы.) Установление этой зависимости для квадрата, правильного треугольника, шестиугольника.
-
Задача по теме: «Окружность и многоугольник».
а) (91) Высота ромба, проведенная из вершины его тупого угла, делит сторону ромба в отношении 1 : 2, считая от вершины его острого угла. Какую часть площади ромба составляет площадь вписанного в него круга?
б) (93) В равнобедренную трапецию с острым углом вписана окружность. Какой процент площади занимает площадь четырехугольника с вершинами в точках касания?
Билет 2.
-
Теорема Пифагора (прямая и обратная).Доказательство одной из них.
-
Правильный многоугольник (определение). Построение правильного четырехугольника, пятиугольника, шестиугольника.
-
Задача по теме «Вписанная окружность».
а) (11) В треугольнике АВС углы А и В равны 38° и 86° соответственно. Найдите углы треугольника, вершинами которого являются точки касания сторон с вписанной в треугольник АВС окружностью.
б) (32). В трапецию вписана окружность радиуса 6. Точка касания делит нижнее основание трапеции на отрезки длины 9 и 12. Найдите стороны трапеции.
Билет 3.
-
Свойства хорд и диаметров. Пропорциональные отрезки в круге. (доказательство)
-
Вывод формулы для вычисления суммы углов выпуклого многоугольника.
-
Задача по теме «Комбинации окружностей».
а) (39) В круговой сектор с углом 60 помещен круг, касающийся дуги сектора и обоих радиусов. Найдите отношение площади сектора и площади круга.
б) (40) Найдите площадь фигуры и длину границы фигуры, являющейся общей частью двух кругов радиуса R каждый, если расстояние между их центрами также равно R.
Билет 4.
-
Параллелограмм (определение). Свойства параллелограмма с доказательством (не менее четырех свойств).
-
Нахождение гипотенузы, катета и острого угла прямоугольного треугольника по данным его второго катета и острому углу.
-
Задача по теме «Углы в окружности».
а) (34) В окружность вписан одиннадцатиугольник, одна из сторон которого равна радиусу окружности, а остальные десять сторон равны между собой. Найдите углы одиннадцатиугольника.
б) (37) На окружности с центром в точке О выбраны точки М и Н. Вторая окружность вдвое меньшего радиуса касается первой в точке М и делит пополам отрезок ОН. Найдите угол ОНМ.
Билет 5.
-
Ромб (определение). Свойства ромба. Признаки ромба.
-
Описанный четырехугольник
-
Задача по теме «Правильные многоугольники».
а) (42) Точка F
лежит на стороне АВ правильного
восьмиугольника ABCDMNPQ
так, что AF
= ![]() ,
FB
=
,
FB
=![]() .
Найдите расстояние от точки F
до прямых, содержащих стороны
восьмиугольника.
.
Найдите расстояние от точки F
до прямых, содержащих стороны
восьмиугольника.
б) (43) ABCDEF – правильный шестиугольник площади S. Какая фигура образуется в пересечении треугольников ACE и BDF? Найдите ее площадь.
Билет 6.
-
Внешний угол треугольника (определение). Теорема о внешнем угле треугольника. Сумма внешних углов n-угольника (док-во).
-
Нахождение значений синуса, косинуса и тангенса угла в 45.
-
Задача по теме «Описанная окружность».
а) (20) В треугольнике АВС АВ = 2, ВС = 3 и угол ВАС в 3 раза больше угла ВСА. Найдите радиус описанной окружности.
б) (16) В треугольнике
АВС
,
АВ = 7, АС = 4![]() .
Найдите расстояние между центрами
окружностей, описанных около треугольников
АСА1
и ВАА1,
где АА1
– высота треугольника АВС.
.
Найдите расстояние между центрами
окружностей, описанных около треугольников
АСА1
и ВАА1,
где АА1
– высота треугольника АВС.
Билет 7.
-
Теорема синусов.
-
Круг (определение). Формула для вычисления площади круга (без вывода). Вывод формулы площади кругового сектора.
-
Задача по теме «Трапеция».
а) (96) Биссектрисы острых углов A и D трапеции ABCD составляют угол 120º и проходят через вершины C и B соответственно. В каком отношении точка пересечения диагоналей трапеции делит каждую ее диагональ?
б) (31). Найдите площадь трапеции с боковыми сторонами 13 и 20 и основаниями 6 и 27.
Билет 8.
-
Теорема косинусов.
-
Окружность (определение). Формула для вычисления длины окружности (без вывода). Вывод формулы длины дуги окружности.
-
Задача по теме «Площади многоугольников».
а) (9) В треугольнике АВС точки А1, В1 и С1 делят стороны ВС, АС и АВ соответственно в отношениях: ВА1 : А1С = 3 : 7; АВ1 : В1С = 1 : 3; АС1 : С1В = 1. Найдите отношение площадей треугольников АВС и А1В1С1.
б) (90) В прямоугольнике АВСD АD : АВ = 5 : 3. На сторонах АВ, ВС, СD и DА выбраны точки Е, F, М и Р соответственно так, что АР : РD = 2 : 3, а ЕFМР – ромб. Найдите отношение площадей прямоугольника и ромба.
Билет 9.
-
Вывод формулы площади треугольника S=½ a·ha . Формула Герона (вывод).
-
Вписанный четырехугольник.
-
Задача по теме «Элементы треугольника».
а) (14) Окружность, диаметром которой служит сторона АС треугольника АВС, проходит через точку пересечения медиан этого треугольника. Найдите отношение длины стороны АС к длине проведенной к ней медианы.
б) (73) Две медианы треугольника равны 3 и 4. В каких пределах может изменяться третья медиана? При каких ее значениях треугольник будет прямоугольным?
Билет 10.
-
Прямоугольник (определение). Свойства прямоугольника (не менее двух). Признаки прямоугольника.
-
Нахождение катета и острых углов прямоугольного треугольника по данным гипотенузе и другому катету.
-
Задача по теме «Пропорциональные отрезки в круге».
а) Найдите расстояние от центра окружности радиуса 9см до точки пересечения двух взаимно перпендикулярных хорд длиной 16см и 14см соответственно.
б) (59) Точка А лежит внутри круга с центром О и радиусом R так, что ОА = a (a < R). Докажите, что для любой хорды MN, проходящей через точку А, выполняется соотношение МА·AN = R² - a².
Билет 11.
-
Вывод формулы радиуса описанной и вписанной окружностей (для треугольника).
-
Вывод формулы площади треугольника: S = ½ ab sin C.
-
Задача по теме «Биссектриса внутреннего угла треугольника».
а) (82) Биссектриса треугольника делит одну из его сторон на отрезки длины 3см и 5см. В каких пределах может изменяться периметр треугольника?
б) Гипотенуза прямоугольного треугольника делится на отрезки 5см и 12см точкой касания вписанной в треугольник окружности. На какие отрезки делит катет треугольника биссектриса его меньшего угла?
Билет 12.
-
Средняя линия треугольника и трапеции (определение). Теоремы о средней линии треугольника и трапеции.
-
Построение окружности, вписанной в треугольник и описанной около него.
-
Задача по теме «Вписанные и описанные окружности».
А) На окружности последовательно расположены точки А, В, С и Д так, что лучи ВА и СД пересекаются под углом 38°, а лучи ДА и СВ – под углом 6°. Найдите углы четырехугольника АВСД.
Б) (18) В треугольнике АВС угол АВС равен 60°. Точка К касания вписанной окружности со стороной АС такова, что АК = 1, СК = 6. Найдите площадь треугольника.
Билет 13.
1. Трапеция (определение). Вывод формулы площади трапеции.
2. Построение касательной к окружности (два случая).
3. Задача по теме “Прямоугольник, квадрат».
А) (83) В квадрате АВСД точка К лежит на стороне ВС, ВК = 4, КС = 2; М – середина ДС. Найдите радиус окружности, проходящей через точки А, К и М.
Б) (92) АВСД – квадрат, К – середина ВС, М – середина СД, Р – точка пересечения АК и ВМ. Найдите угол СРМ.
Билет 14.
-
Вывод формулы площади параллелограмма S= a·ha; S=½ d1·d2·sin (d1d2).
-
Описанный четырехугольник.
-
Задача по теме «Решение треугольников».
А) (76) На сторонах прямоугольного треугольника с катетами 6 и 8 построены квадраты, лежащие вне треугольника. Найдите площадь треугольника с вершинами в центрах этих квадратов.
Б) (123) Докажите, что длина АА1 – биссектрисы треугольника АВС – вычисляется из соотношения АА1² = АВ·АС – А1В·А1С.
Билет 15.
1. Теорема Фалеса.
2. Вписанные углы. Теорема о связи между величинами вписанного и соответствующего ему центрального угла.
3. Задача по теме “Прямоугольный треугольник”.
А) (5) Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два треугольника, площади которых равны соответственно 6 см² и 54 см². Найдите гипотенузу треугольника.
Б) (7) Найдите площадь прямоугольного треугольника, если биссектриса прямого угла делит гипотенузу на отрезки длины 15см и20 см.
ВОЗМОЖНЫЕ ЗАДАЧИ
-
Задача по теме «Комбинации с окружностями».
А) (13) Круги радиусов 1, 6, и 14 касаются друг друга. Найдите радиус окружности, вписанной в треугольник с вершинами в центрах данных кругов.
Б) (107) Каждая из вершин правильного треугольника со стороной a является центром круга радиуса a. Найдите площадь общей части трех кругов.
-
Задача по теме Элементы треугольника»,
А) (56) Докажите, что биссектриса АА1 треугольника АВС вычисляется по формуле
АА1
=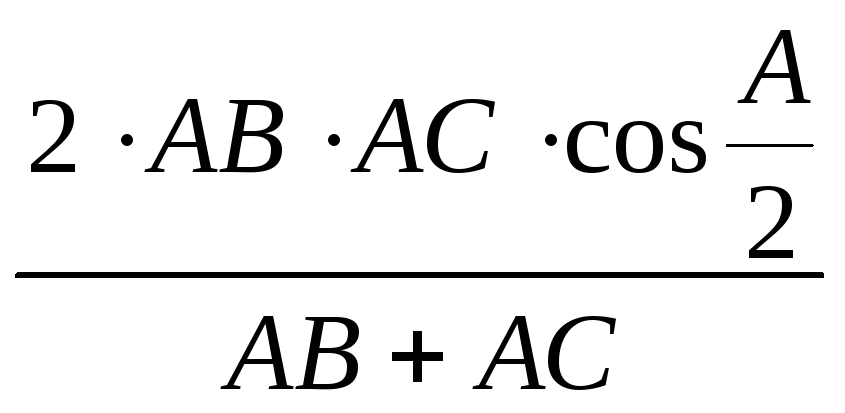
Б)
(57)Докажите, что медиана треугольника
со сторонами a,
b, c, проведенная
к стороне a,
вычисляется
из соотношения
![]()
