1.2.3. Формула полной вероятности.
Пусть
– полная группа несовместных событий(их
называют гипотезами),. 
– некоторое событие , которое может
произойти вместе с одной из гипотез.
Формула полной вероятности имеет вид
Задачи:
Два датчика посылают сигналы в общий канал связи, причем первый посылает сигналы в два раза чаще второго. Вероятность получить искаженный сигнал от первого датчика равна 0,06 , а от второго – 0,03 . Какова вероятность того, что наудачу выбранный сигнал из общего канала связи окажется искаженным?
Один ведущий самолет и два ведомых посланы на бомбометание. Радионавигационное оборудование есть только у ведущего самолета. Оборона противника уничтожает каждый самолет с вероятностью 0,2 . Бомбометание ведется каждым самолетом независимо, при этом цель поражается с вероятностью 0,3 . Найти вероятность поражения цели.
В группе спортсменов имеется 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму для лыжника равна 0,9, для велосипедиста – 0,8, для бегуна –0,75. Найти вероятность того, что наугад выбранный спортсмен выполнит квалификационную норму.
В клинику поступают в среднем 50% сердечно–сосудистых больных, 30% – с заболеваниями легких и 20% – с заболеваниями почек. Вероятность полного излечения больного первой группы равна 0,1, больного второй группы – 0,7, и третьей группы – 0,5. Найти вероятность того, что больной поступивший в клинику, будет выписан здоровым.
1.2.4. Формула вероятностей гипотез Байеса.
Формула
Байеса вычисляет вероятности каждой
из гипотез, после появления события 
и имеет вид
Она используется для решения задач диагностики.
Задачи:
Исследование больного вызвало предположение о возможности трех заболеваний с вероятностями
.
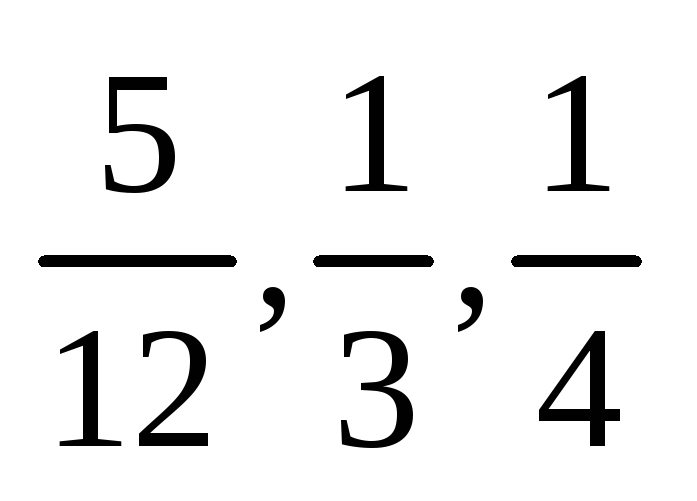Для уточнения диагноза был проведен
анализ, давший дополнительный результат
с вероятностью 0,3; 0,9 и 0,1 при первом,
втором и третьем заболевании,
соответственно. Какова после этого
вероятность каждого из заболеваний?Три охотника выстрелили по кабану, который оказался убитым одной пулей. Вычислить вероятность, что кабан убит каждым из охотников, если вероятности попадания для них равны 0,2 ; 0,4 и 0,6.
Указания:
Обозначим
– кабан убит одной пулей, 
–
кабан убит первым охотником, 
–
кабан убит вторым охотником, 
–
кабан убит третьим охотником, 
–
одиночное попадание первого охотника,
–
одиночное попадание второго охотника,
–
одиночное попадание третьего охотника.
Таким образом, гипотезы выражаются
формулами – 
.
Число грузовых машин, проезжающих мимо АЗС, относится к числу проезжающих там же легковых машин как 3:2. Вероятность того, что будет заправляться грузовая машина равна – 0,1. Для легковой машины эта вероятность – 0,2. На заправку подъехала машина. Найти вероятность того, что она грузовая.
1.2.5. Повторение опытов. Схема Бернулли.
Ситуация,
в которой производится n
независимых опытов, в каждом из которых
с одной и той же вероятностью 
может появиться некоторое событие 
носит название – схема Бернулли.
Требуется вычислить вероятность
появления события 
в n
опытах m
раз. Обозначается такое событие 
,
а его вероятность – 
.
Конструкция события 
выглядит следующим образом
Общее
число слагаемых равно 
(число сочетаний из n
по m),
поэтому
Это
выражение называется – формула Бернулли.
Следует обратить внимание на тот факт,
что вероятности 
представляют собой члены разложения
бинома 
.
В
более сложной ситуации событие 
появляется в каждом опыте со своей
вероятностью. В опыте с номером i
вероятность появления равна 
,
а вероятность не появления равна 
.
Для вычисления вероятностей 
используется так называемая производящая
функция 
,
у которой коэффициенты при 
и есть вероятности 
.
Задачи:
Производится три выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,4. Какова вероятность двух попаданий?
Указания:
По формуле Бернулли искомая вероятность равна
Для решения задачи необходимо воспользоваться встроенной функцией ЧИСЛКОМБ из категории Математические. В качестве аргументов этой функции следует указать адреса ячеек, в которых предварительно записывается общее число вариантов и число выбранных вариантов.
По удаляющемуся автомобилю с преступниками производится четыре независимых выстрела. Вероятности попаданий при этих выстрелах равны
.
Найти вероятности ни одного, одного,
двух, трех и четырех попаданий.
Указания:
Следует воспользоваться производящей функцией, которая имеет вид
